| Рис. 3.5. Внешне случайное поведение цены согласно логистическому отображению |  |
Прогноз посредством сети О Логистическое отображение [c.83]
| Рис. 3.7. Прогноз логистического отображения с помощью 1-2-1 сети | 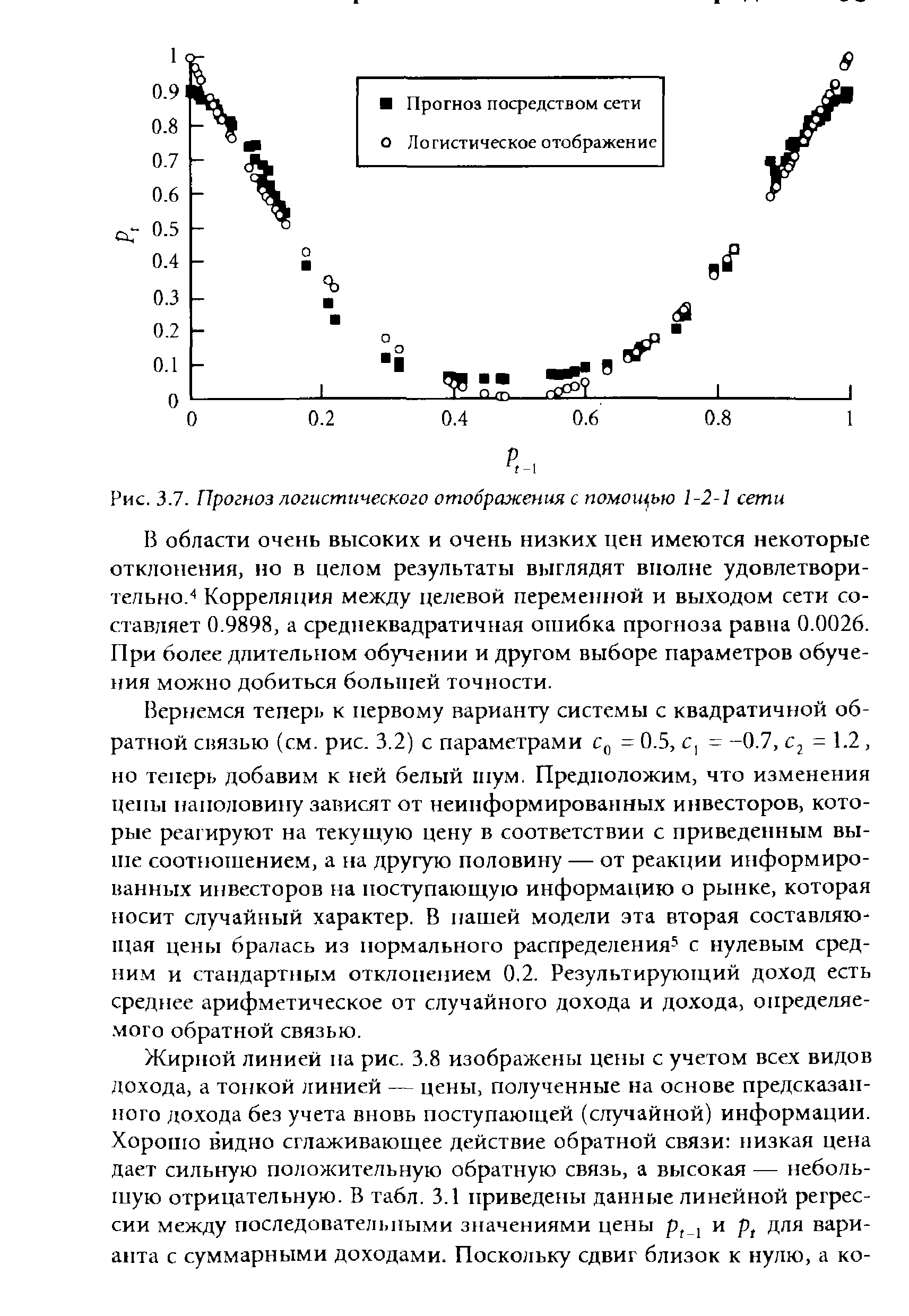 |
Пример 1. Рассмотрим так называемое логистическое отображение [c.217]
Из этой таблицы видно, что величины (хп), порожденные логистическим отображением с А = 4, практически можно считать некоррелированными, и в этом смысле последовательность (хп) может быть названа " хаотическим белым шумом". [c.221]
Для отображения основной тенденции развития явлений во времени применяются различные уравнения, полиномы разной степени, экспоненты, логистические кривые и другие функции. [c.80]
Логистические задачи, которые возникают в практической деятельности, решать простейшими арифметическими методами или на основе опыта работы невозможно. Это связано с тем, что возникает множество возможных вариантов. Так, при трех поставщиках продукции и ее трех потребителях возможно 90 различных вариантов решения, а при четырех поставщиках и четырех потребителях число возможных вариантов решения составит уже более 6000 и т.д. Какой вариант более целесообразен Для того чтобы ответить на этот вопрос, необходимо составить математическую модель. Математическая модель — это абстрактное отображение с помощью математической символики реального процесса. [c.133]
Имеющийся практический опыт показывает, что основной отличительной чертой форм и технологий экономико-математического моделирования логистических процессов является максимально возможное отображение результатов их производственно-хозяйственной деятельности. Это дает возможность не только осуществлять необходимые оценки с очень высокой степенью точности и на основе этого принимать соответствующие управленческие решения, но и рационализировать сам процесс управления. [c.129]
Этот тип уравнения является замечательным обучающим инструментом, потому что он производит статистически случайные числа детерминировано. Однако в качестве инструмента для рыночного или экономического анализа это уравнение не очень полезно. Итеративные отображения, подобные логистическому уравнению, обнаруживают хаос один раз на итерацию то есть длина их памяти чрезвычайно коротка. Они не обнаруживают такие типы циклов, которые мы видим в экономике или инвестициях. [c.100]
Графический Графическое представление возможных каналов распределения по типу сырья или товара Отсутствие оценочных параметров анализа и проектирования каналов распределения Невозможность отражения зигзагов канала распределения Отсутствие механизма выбора наиболее эффективного канала Возможность расположения участников каналов распределения в соответствии с движением товарно-материального потока (в логистической последовательности) Наглядность отображения многообразных связей распределительного канала [c.163]
Логистическая форма тренда подходит Для отображения развития во всех его [c.151]
Если с0 =0.5, j =-0.7, с2 = 1.2, то по значениям цены (предполагается, что они лежат в интервале от 0 до 1) в предыдущий момент времени можно вычислить текущую цену. На рис. 3.2 показана так называемая логистическая кривая1 (или логистическое отображение), получающаяся при выбранных значениях параметров. Для цен ниже 0.4 видна сильная положительная обратная связь, тогда как для цен выше 0.4 имеется менее сильная отрицательная обратная связь. [c.77]
До сих пор в наших экспериментах рассматривались только задачи с одним входным переменным рм. Теперь мы обратимся к проблеме, которая аналогична только что рассмотренному одномерному логистическому отображению, но, в отличие от него, имеет двумерный вход. Впервые эта модель была рассмотрена Хеноном [139] и получила название отображения Хенона. Уравнения модели таковы [c.84]
Как xt, так и yt зависят от предыдущих значений xt t и yt p и это делает систему динамической. Из-за квадратичного члена в первом уравнении система является нелинейной. Если мы возьмем произвольные начальные значения и сгенерируем по этим уравнениям ряд значений для xt и yt, то окажется, что их значения беспорядочно и внешне случайно располагаются, соответственно, в интервалах от -0.4 до 0.4 и от -1.4 до 1.4. Так же, как и в рассмотренном ранее случае логистического отображения рис. 3.4, эти значения не сходятся к какому-либо положению равновесия и не совершают периодических колебаний. Таким образом, мы имеем дело с системой, обладающей странным аттрактором. Понятно, что с помощью традиционных статистических методов нам вряд ли удастся выявить структуру модели, поскольку и х, и у ведут себя беспорядочно (см. [214, с. 152]). [c.84]
Логистическая кривая имеет форму латинской буквы s положенной на бок, отчего еще называется эсобраэной кривой. Она имеет два перегиба от ускоряющегося роста к равномерному (вогнутость) и от равномерного роста посреди периода к замедляющемуся (выпуклость). Она подходит для отображения развития в течение длительного периода, проходящего все фазы, например процесса насыщения потребителей каким-то новым товаром, скажем, телевизорами сначала медленный, но все ускоряющийся рост доли семей, [c.325]
Нелинейные динамические системы являются детерминированными системами, которые могут проявлять беспорядочное поведение. При обсуждении хаоса обычно обращаются к хаотическим отобралсениям. Отображения обычно представляют собой системы итерированных разностных уравнений, таких как известное логистическое уравнение [c.100]
Отображение Хенона может быть представлено как двумерная система в электронной таблице. Отображением, демон-стрирющим другой тип поведения, является так называемое логистическое уравнение с задержкой [c.172]
Смотреть страницы где упоминается термин Логистическое отображение
: [c.248] [c.226] [c.482] [c.520] [c.370]Основы стохастической финансовой математики Т.2 (1998) -- [ c.217 ]
