Одна из главных заслуг Эллиота — применение последовательности и отношений Фибоначчи. Возможность прогнозировать вероятные длины волн с помощью точных вычислений является существенным преимуществом волновой теории. [c.134]
Вначале кратко излагаются основные принципы волновой теории Эллиота и отношения Фибоначчи, создавая общий фон подачи материала книги Новые методы торговли по Фибоначчи . Далее эксперт по Фибоначчи Роберт Фишер переходит к сути концепции, исследуя шесть геометрических инструментов для торговли по Фибоначчи [c.3]
Однако это отношение иррационально оно имеет бесконечную, непредсказуемую последовательность десятичных значений, выстраивающихся после него. Оно никогда не может быть выражено точно. Если каждое число, являющееся частью ряда, разделить на предшествующее значение (например, 13-Л8 или 21 -ИЗ), результат действия выразится в отношении, которое колеблется вокруг иррационального числа 1,61803398875..., чуть больше или чуть меньше соседних отношений ряда. Отношение никогда, до бесконечности, не будет точным до последней цифры (даже при использовании самых мощных компьютеров, созданных в наше время). Ради краткости, будем использовать в качестве отношения Фибоначчи число 1,618 и просим читателей не забывать об этой погрешности. [c.10]
Мы подразделили наши наблюдения на два раздела. Сначала кратко пройдемся по отношению Фибоначчи и его присутствию в природных явлениях и архитектуре. Затем кратко опишем, как используют отношение Фибоначчи в математике, физике и астрономии. [c.11]
Отношения Фибоначчи в природе [c.11]
Чтобы оценить огромную роль отношения Фибоначчи как природной константы, достаточно лишь взглянуть на красоту окружающей нас природы. Рост растений в природе — идеальный пример общей уместности отношения Фибоначчи и базового ряда суммирования Фибоначчи. Числа Фибоначчи можно найти в количестве ответвлений на стебле каждого растущего растения и в числе лепестков. [c.11]
При анализе мировых рынков и разработке стратегий торговли мы ищем структуры или фигуры графиков, прибыльные в прошлом (согласно историческим данным). Следовательно, они должны иметь вероятность дальнейшего успеха в будущем. Мы полагаем, что нашли такую структуру или общую фигуру в отношении Фибоначчи ФИ. [c.12]
Отношение Фибоначчи ФИ иррациональное число. Мы никогда не будем знать его точное значение до последнего знака. Поскольку величина погрешности при округлении отношения Фибоначчи ФИ становится меньше по мере роста ряда суммирования Фибоначчи, мы рассматриваем 8 как самое малое из всех чисел ряда суммирования Фибоначчи, которое может быть с толком использовано для рыночного анализа (возьмите, к примеру, частные значения 13-г 8 = 1,625 и 21-НЗ = 1,615 в сравнении с ФИ= 1,618). [c.12]
В разное время и на различных континентах люди пытались успешно включать в свою работу отношение ФИ как закон точной пропорции. Не только египетские пирамиды построены, согласно отношению Фибоначчи ФИ (более подробное описание см. в книге "Приложения и стратегии Фибоначчи для трейдеров"), но тот же самый феномен находим и в мексиканских пирамидах. [c.12]
Поперечное сечение пирамиды — это структура, сформированная в виде лестницы. Есть 16 ступеней в первом пролете, 42 ступени во втором и еще 68 ступеней в третьем. Эти числа следующим образом связаны с отношением Фибоначчи 1,618 [c.14]
Здесь мы находим (хотя и не с первого взгляда) отношение Фибоначчи ФИ в макроструктуре, знакомой всем нам. Наша задача - перенести этот подход из природы и окружающей среды человека в сферу графиков и рыночного анализа. В нашей рыночной среде следует задаться вопросом, сможем ли мы, и если "да", то где обнаружить ФИ столь же полно и наглядно, как в естественной жизни растений и искусственных пирамидах. [c.14]
Отношения Фибоначчи в геометрии [c.14]
ФИ-спираль и ФИ-эллипс имеют необычные свойства, которые в соответствии с отношением Фибоначчи ФИ находятся в двух измерениях цена и время. Весьма вероятно, что интегрирование ФИ-спирали и ФИ-эллипса намного повысит уровень интерпретации и использования отношения Фибоначчи. До сих пор отношение ФИ Фибоначчи в основном использовалось как инструмент для измерения коррекций и расширений ценовых колебаний. Прогнозы времени интегрировались редко, потому что они не представлялись столь же надежными, как анализ цен. Но с включением в геометрический анализ ФИ-спиралей и ФИ-эллипсов обе части — и ценовой, и временной анализ — могут комбинироваться правильно. [c.14]
Держа в уме представление отношения Фибоначчи ФИ в одномерной (линия) и двумерной (прямоугольник) геометрии, можно перейти к более сложным геометрическим объектам. Они подведут ближе к инструментам, которые мы хотим применять для анализа параметров времени и цены фондовых и фьючерсных рынков. [c.15]
ФИ-спираль — связующее звено между рядом суммирования Фибоначчи, вытекающим из него отношением Фибоначчи ФИ, и волшебством природы, которое мы видим вокруг нас. [c.17]
Эллиот не понимал, что важна не нумерация волн, а ФИ Фибоначчи. Отношение Фибоначчи — закон природы и человеческое поведение. При наблюдении колебаний рынка мы пытаемся измерить не больше и не меньше, чем ФИ Фибоначчи. В то время как ряд суммирования Фибоначчи и отношение Фибоначчи ФИ постоянны, нумерация волн вводит в заблуждение. [c.23]
Мы представим и другие инвестиционные стратегии, близко связанные с отношением Фибоначчи. Мы охватим коррекции и расширения, как это делал Эллиот, но сделаем это по-другому, всегда фокусируясь на отношении Фибоначчи ФИ и его представлении в инструментах, которые мы анализируем. [c.25]
Мы связываем закон природы, выраженный на математическом языке через отношение Фибоначчи ФИ, с колебаниями рынка, как проиллюстрировано на рисунке 1.15. [c.27]
Когда мы знаем расстояние от пика А до пика В в днях (или иных единицах времени), мы можем умножить это расстояние на отношение Фибоначчи ФИ = 1,618, чтобы предсказать точку С, которая будет достигнута в тот день [c.27]
Рассматривая расширения как графические инструменты для рыночного анализа, мы снова используем отношение Фибоначчи, полученное нами из ряда суммирования Фибоначчи (рисунок 1.17). [c.29]
Хотя никакого рационального объяснения отношения Фибоначчи не существует, применяя это отношение в качестве схемы анализа, можно уловить сильные крупные движения рынка, вызванные новостями политического или экономического характера, докладами об урожае или складских запасах или любой ситуацией, в которой поступки совершаются под воздействием эмоций. Страх или жадность, быстрые рынки или стоп-ордера заставляют рынки двигаться. Мы измеряем степень этих движений, используя отношение Фибоначчи ФИ, ряд суммирования Фибоначчи и элементные числа соответствующего ряда ФИ. [c.29]
Каждое число, являющееся частью ряда суммирования Фибоначчи, при делении его на предшествующее значение (например, 13+8 или 21-ИЗ) дает отношение, которое мы округленно выражаем, как ФИ = 1,618 (зная, что осцилляция чисел последовательности Фибоначчи к отношению Фибоначчи ФИ асимптотический процесс). [c.37]
И коррекции, и расширения — мощные торговые инструменты, если осуществляется их правильная привязка к ряду суммирования Фибоначчи и соответствующему отношению Фибоначчи ФИ. [c.48]
Разделы с А по С описывают использование коррекций в качестве торговых инструментов. Сначала коррекции будут связываться с отношением Фибоначчи ФИ в принципе, а затем применяться как инструменты построения графиков на наборах дневных и недельных данных для различных продуктов. [c.48]
В разделах D и Е объясняются расширения и их связь с отношением Фибоначчи ФИ на основе 3-волновых и 5-волновых рыночных фигур. В разделе F примеры в 5-волновых фигурах иллюстрируют аналитическую силу расширений как инструментов торговли в комбинации с числами базового ряда суммирования Фибоначчи. [c.48]
Минимальный размер колебания необходим, чтобы наилучшим образом использовать в коррекции отношение Фибоначчи [c.51]
На рынке наличной японской иены, например, нам требуется подтверждение размера колебания в 200 базисных пунктов при работе с отношениями Фибоначчи в коррекциях 38,2, 50,0 или 61,8%. Однако коррекция 38,2% в колебании в 200 базисных пунктов (что означает 76 тиков) может оказаться слишком мелкой для работы, потому что колебание в 200 тиков и соответствующие коррекции в 76 тиков могут происходить на волатильных рынках один или два раза в неделю. [c.51]
Для вычисления целевой прибыли берем полную амплитуду первой импульсной волны и умножаем ее на одно из вышеупомянутых отношений Фибоначчи (рисунок 3.5). [c.53]
Размер колебания должен быть умножен на отношение Фибоначчи ФИ, где ФИ = 1,618. [c.67]
Если размер колебания слишком мал, импульс расширения может оказаться слишком большим, и рынок пройдет на большое расстояние за целевую цену. Это делает ненадежным отношение Фибоначчи ФИ = 1,618, используемое для вычисления ценовой цели. Кроме того, на рынке может быть слишком много шума, что может сделать базовые рыночные колебания непредсказуемыми. И еще более важно если размер колебания слишком мал, целевые прибыли могут сократиться настолько, что их станет трудно выполнить. [c.67]
Чтобы проанализировать 3-волновую фигуру, мы умножали величину первой импульсной волны на отношение Фибоначчи 1,618. Полученное произведение прибавляли к размеру колебания первоначального движения. Таким образом, вычислялась линия ценовой цели Фибоначчи. Именно на этой линии мы ожидали разворота третьей волны. [c.75]
В правильном 5-волновом движении восходящего тренда линия ценовой цели конца волны 5 рассчитывается умножением амплитуды волны 1 на отношение Фибоначчи ФИ = 1,618 и затем умножением амплитуды от основания волны до вершины волны 3 на обратное значение отношения Фибоначчи ФИ (ФИ = 0,618). В нисходящем тренде также умножаем первоначальный размер колебания на 1,618 и умножаем амплитуду от максимума волны 1 до минимума волны 3 на отношение 0,618. [c.76]
Анализ расширений 3-волновых фигур заставил нас сомневаться в возможности многократного подтверждения ценовых целей дополнительными отношениями Фибоначчи. Если теперь интегрирование 5-волновых движений позволит нам вычислять коридоры целевых цен Фибоначчи, инвесторы получат очень хорошее указание, какую ценовую цель использовать. Пока верхняя и нижняя границы ценовой полосы находятся близко друг к другу, можно использовать их как достоверные ценовые индикаторы. [c.76]
О моей неудачной попытке пополнить свои знания в области теории волн Эллиота лучше всего говорят два не связанных друг с другом события. Я пригласил одного из врачей в Висконсин, чтобы он поделился с моими коллегами опытом использования волнового анализа. Когда я приехал в аэропорт, самолет уже приземлился и пассажиры вышли, но моего врача нигде не было. Я позвонил в его офис, чтобы узнать, не опоздал ли он на самолет. Секретарша уверила меня, что он вылетел (она сама его провожала) и что он обязательно найдет меня. В конце концов ко мне подошел человек и спросил "Вы Том " Он заявил, что сразу меня узнал, поскольку в траектории, которую я описывал, блуждая по аэропорту, просматриваются углы Фибоначчи. Я сразу понял, с кем имею дело, и во мне зародилось дурное предчувствие. Оно меня не подвело встреча оказалась абсолютно пустой и безрезультатной. На этом я не сдался, но решил побеседовать со вторым специалистом в области теории волн сначала по телефону, прежде чем приглашать его в Висконсин. Жизнь подтвердила мудрость этого шага. Оказалось, что доктор является страстным поклонником Эллиота и Фибоначчи и что его жизнь полностью основывается на их теориях. В частности, он был три раза женат, у него пять детей, он работает восемь дней подряд, а затем тринадцать дней отдыхает. Я все понял и решил самостоятельно заняться изучением предмета. Я был уверен, что в указанных теориях есть "жемчужное зерно", но мне предстояло найти его самостоятельно. В конце концов последовательность Фибоначчи лежала в основе самых разных явлений начиная от Ед-ипетских пирамид и кончая пересчетом километров в мили. Однако ее роль, равно как и роль теории волн в развитии рынков предстояло еще выяснить. Мой подход к использованию отношений Фибоначчи в расчете величины коррекции уже был описан в главе 2. В этой главе я остановлюсь на применении разработанных мной методик волнового анализа. [c.75]
Возможно, в будущем вы пожелаете потратить часть своей торговой прибыли на путешествия к великим культурным центрам настоящих и прошлых цивилизаций. В таком случае вы вскоре обнаружите, как это произошло со мной, что отношения Фибоначчи свойственны архитектуре Афин, Рима, Амстердама, Парижа, Египта, многих областей Южной Америки и так далее. Существует элементный резонанс в том, как эти эстетически приятные формы возникают из математических выкладок. [c.126]
Вы можете наблюдать любопытную эволюцию расширений Фибоначчи в музыкальных произведениях, кристаллических образованиях и даже в процессе прироста поголовья кроликов. Отношения Фибоначчи находятся в изобилии повсюду, будь то спираль ДНК, определенная конструкция сот в пчелином улье или вдохновляюще грандиозная пирамида в Гизе. Само человеческое тело пример соотношений Фибоначчи. Недавно на одном из своих семинаров я встретил хирурга, защитившего диплом по теме восстановления лица. Цель его работы - количественно связать послеоперационный успех пластической хирургии с тем, насколько близко восстанавливаемые кости приближаются к "Золотой Середине". Невозможно отрицать, что отношения Фибоначчи и числа, генерирующие их, присущи всей материи. [c.127]
Я мог бы очень долго распространяться о поэзии соотношений Фибоначчи, но в этом случае никогда не добрался бы до их практического применения на рынках. Если вы хотите исследовать этот предмет поподробнее, существует много книг, написанных для обсуждения более эзотерических аспектов1. Конечно, в них лучше описаны математические выкладки, чем это делаю я. Кроме того, мой уход от темы может вызвать недовольство у некоторых людей. Поэтому я оставляю поэзию, происхождение и историю чисел и отношений Фибоначчи другим. Эта книга о практическом применении концепций Фибоначчи на рынке, и в этом ключе я возвращаю нас к действительности и повторяю следующий запрет для тех, кто раньше перескочил сразу к этой главе. [c.129]
Это отношение стало обрастать разными особыми именами еще даже до того, как другой средневековый математик Лука Па-чиоли (1445—1514) назвал его "божественной пропорцией". Среди его современных названий — "золотое сечение" и " золотая середина". Немецкий астроном Иоганн Кеплер (1571 — 1630) назвал отношение Фибоначчи одним из сокровищ геометрии. В алгебре оно, как правило, обозначается греческой буквой ФИ (ср), а именно [c.10]
Существование отношения Фибоначчи ФИ в геометрии очень хорошо известно. Однако подходящий для инвесторов способ применения этого отношения как геометрического инструмента к движению биржевых цен с использованием ФИ-спиралей и ФИ-эллип-сов до настоящего времени не публиковался. Чтобы применять ФИ-спирали и ФИ-эллипсы как аналитические инструменты, требуются квалификация программиста и сила компьютеров. [c.14]
Сторона АВ квадрата AB D на рисунке 1.4 делится пополам. Чертится дуга круга с центром в точке Е и радиусом ЕС, отсекающая продление АВ в точке F. Перпендикулярно AF чертится линия FG, пресекающая продление D в точке G. AFGD — золотой прямоугольник. Согласно формальному определению, геометрическое представление золотого сечения в прямоугольнике означает, что длина прямоугольника этой формы в 1,618 раз больше, чем его ширина. И вновь появляется отношение Фибоначчи ФИ, на сей раз в пропорциях золотого прямоугольника. [c.15]
Эти шесть инструментов (1) сам ряд суммирования Фибоначчи, (2) временные цели Фибоначчи, (3) коррекции и расширения в связи с отношением Фибоначчи, (4) ФИ-каналы, (5) ФИ-спира-ли и (6) ФИ-эллипсы. [c.25]
Наш анализ времени основан на открытиях Евклида Мегар-ского и изобретенном им золотого сечения. Об этом уже говорилось ранее в представлении отношения Фибоначчи в геометрии и золотого сечения линии. [c.27]
| Рисунок 3.16 Расширение в 3 волне восходящего тренда 3-волновой фигуры. Уровень ценовой цели измерен отношением Фибоначчи ФИ = 1,618. Источник FAM Resear h, 2000. | 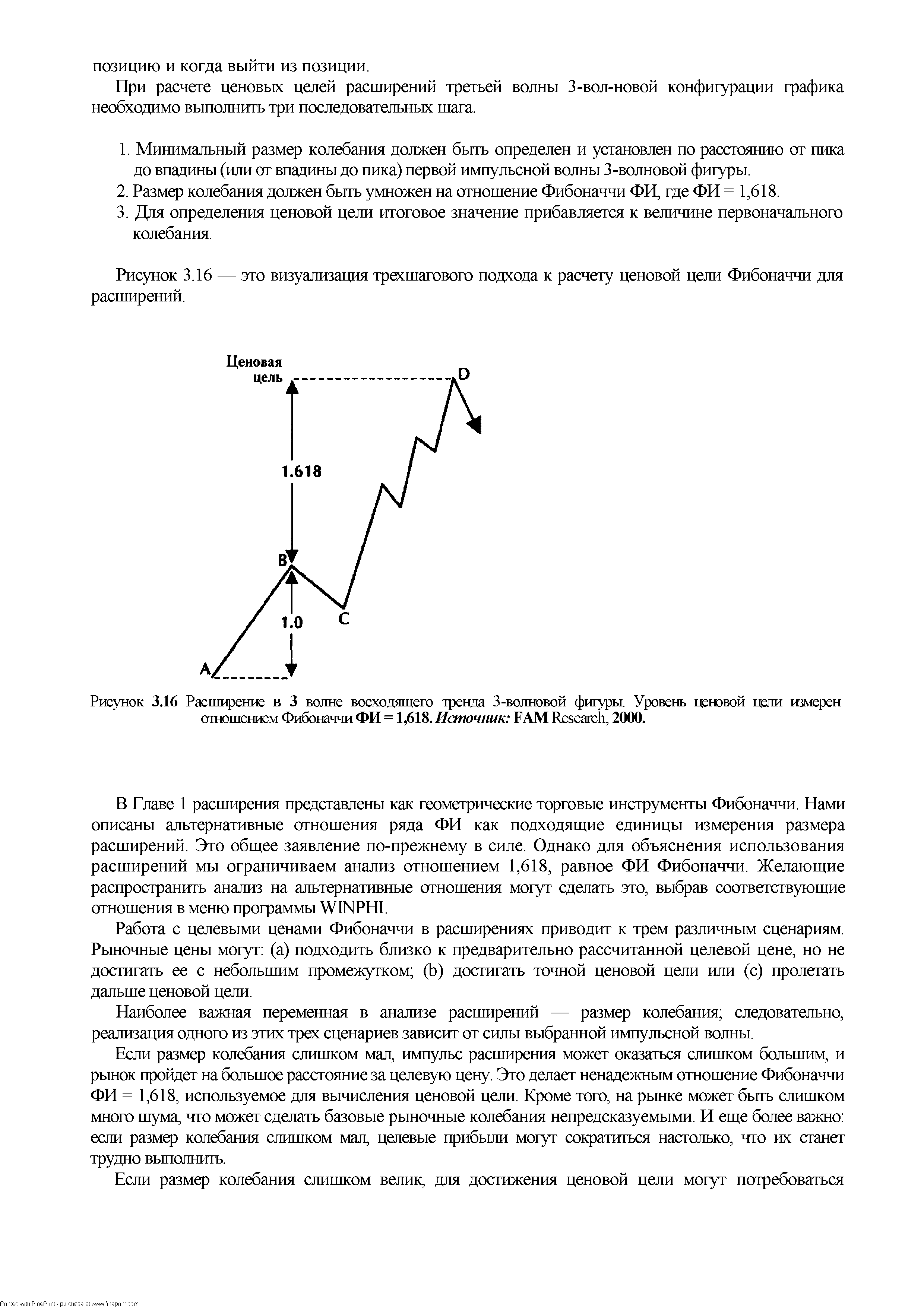 |
