Числа Фибоначчи и теория волн Эллиотта [c.64]
Числа Фибоначчи и Теория Волн Эллиотта [c.102]
Математической основой теории волн Эллиота являются числа Фибоначчи (см. стр. 206). Не вдаваясь в детали, скажем лишь, что ряд Фибоначчи начинается с единицы, а каждый последующий элемент ряда получается простым суммированием двух предыдущих членов (напр., 0+1=1, 1+1=2, 2+1=3, 3+2=5, 5+3=8, 8+5=13 и т.д.). Полный набор волн любого цикла в теории Эллиота является одним из элементов ряда Фибоначчи. Например на предыдущем графике изображены две основные волны (импульсная и корректирующая), 8 промежуточных волн (последовательность 53 , показанная на первом графике) и 34 малые волны (они отмечены на втором графике). Числа 2, 8 и 34 являются членами ряда Фибоначчи. [c.69]
На практике для предсказания продолжительности и величины будущего рыночного движения, которое может длиться от нескольких минут или часов до нескольких лет и десятилетий, аналитики используют волновые модели Эллиота в комбинации с числами Фибоначчи. [c.69]
Существует четыре распространенных инструмента технического анализа, основанных на числах Фибоначчи это дуги, веера, уровни коррекции и временные зоны. Общий принцип интерпретации этих инструментов состоит в том, что при приближении цены к построенным с их помощью линиям следует ожидать изменений в развитии тенденции. [c.247]
Восстановления, часто используемые в торговле, включают 25, 33, 50, 75 и 88%. Кроме того, многие трейдеры используют "числа Фибоначчи", названные по имени итальянского математика ХП века. В рядах Фибоначчи обычно используются два процентных значения — 61,8 и 38,2%. [c.59]
В дополнение к процентам, описанным выше, существуют и другие популярные среди трейдеров уровни восстановления, а именно 38,2 и 61,8%, в сочетании с упомянутым ранее уровнем 50%. Это числа Фибоначчи, названные по имени европейского математика, изучавшего числовые ряды в XII веке. Он придумал свой ряд, добавляя первое число ко второму, второе к третьему и так далее (1, 1, 2, 3, 5, 8, 13, 21...) Эта последовательность получила название "ряд Фибоначчи" и используется применительно к архитектуре, растениям, человеческому организму и, конечно, рынку. При изучении рядов Фибоначчи обычно используются два процентных значения 61,8 и 38,2%, которые также применяются к восстановлениям на рынке. [c.148]
Мир буквально наводнен соотношением 0,618. Размещение семян в цветках представляют собой числа Фибоначчи. Сердечная мышца сокращается до 0,618 от своей изначальной длины. Совершенную структуру, определяемую соотношением 0.618, демонстрирует раковина моллюска Наутилус. Более интимный пример - пупок у человека расположен на уровне 0.618 от его полного роста. Написаны целые тома, представляющие и систематизирующие случаи наличия соотношения 0.618 в природе. [c.42]
Некоторые из перечисленных индикаторов являются несколько мистическими. Трудно, например, поверить, что числа Фибоначчи лежат в основе изменения цен акций, хотя есть работы, выявляющие их корреляции. Изучению этих и других индикаторов можно не без пользы посвятить много времени, но все они имеют общий недостаток они содержат некоторые параметры, которые выбираются по вкусу автора (например, число дней в динамических средних). Чтобы уточнить эти параметры, фактически для каждых акций нужно проводить маленькое исследование. Реально же у трейдера не так много времени, чтобы анализировать графики цен акций множеством различных методов, да еще размышлять при этом о применимости данного индикатора и о значении параметров, которые в него входят. Приобретя некоторый опыт, трейдер использует в основном один или два индикатора, которые он чувствует лучше всего. Эти индикаторы служат ему аналитической базой, а далее он полагается на свой опыт, данные о состоянии рынка и фундаментальные показатели. [c.186]
Я не буду утомлять читателя длинными пассажами о числах Фибоначчи, лежащих в основе окружающего нас мира, а просто сошлюсь на многочисленные учебники и статьи, посвященные описанию этой числовой последовательности и так называемого золотого сечения. Я лишь еще раз подчеркну важность числовой последовательности Фибоначчи, включающей в себя следующие числа 1,2, 3, 5, 8, 13, 21, 34, 55 — и т. д. Каждое последующее число ряда получается путем сложения двух предыдущих чисел. По мере роста номера числа в последовательности отношение предшествующего числа к последующему приближается к 0,618, а отношение последующего числа к предшествующему стремится к 1,618. Такая особенность присуща только членам данной последовательности. [c.46]
Еще более важным является индикатор, показывающий скорость изменения данных процентных величин. На своем опыте я убедился, что этот индикатор является наиболее надежным с точки зрения определения наиболее перспективных объектов инвестиций. Скорость изменения рассчитывается просто разделите процентную величину текущего дня на процентную величину X дней тому назад. Обычно я работаю с числами Фибоначчи. Выбрав определенное число, я рассчитываю скорость изменения путем деления сегодняшней величины на величину, отстоящую от сегодняшней, по крайней мере, на четыре уровня Фибоначчи в сторону уменьшения. Допустим, я использую ряд из 89 дней. Чтобы рассчитать скорость изменения, мне нужно сравнить сегодняшнюю величину с величиной 13 дней тому назад — в последовательности Фибоначчи числа возрастают от 13 до 21, 34, 55 и затем до 89. Легко увидеть, что число 13 расположено на четыре уровня ниже, чем число 89. Если бы вы использовали ряд из 144 дней, то нужно было бы сравнивать величину текущего дня с величиной 21 день тому назад если бы вы использовали ряд из 233 дней, то нужно было бы сравнивать величину текущего дня с величиной 34 дня тому назад. Имейте в виду, что это всего лишь рекомендации. Возможно, вы добьетесь лучших результатов, если будете использовать другую числовую последовательность или если для расчета скорости изменения вы выберете другие временные периоды. Но как только период выбран, он должен быть одним и тем же для всех сравниваемых ценных бумаг. Например, если для одного наименования акций выбран 89-дневный период и скорость изменения рассчитывается на основе процентной величины 13 дней назад, тогда те же самые временные отрезки должны использоваться при оценке относительной привлекательности других акций (см. рис. 5.9). [c.90]
С марта по начало мая включительно рынок находится в сильном восходящем Тренде, что определено с помощью 3x3. Поэтому мы играли бы в длинную сторону, покупая на падениях, основываясь, скорее всего, на часовом графике, и продавая на определенных целевых точках. Эти падения и Целевые Точки определяются числами Фибоначчи, что будет рассмотрено позже. [c.46]
Возможности этого пути иллюстрирует приведенное ниже сравнение предсказаний двух типов комитетов из 25 экспертов (см. Рисунок 14 и Рисунок 15). Предсказания проводились по одной и той же схеме в качестве входов использовались экспоненциальные скользящие средние приращений ряда с периодами равными первым 10 числам Фибоначчи. По результатам 100 экспериментов взвешенное предсказание дает в среднем превышение правильно угаданных знаков над ошибочным равное примерно 15 тогда как среднее - около 12. Заметим, что общее число повышений курса над понижением за указанный период как раз равно 12. Следовательно, учет общей тенденции к повышению в виде тривиального постоянного предсказания знака "+" дает такой же результат для процента угаданных знаков, что и взвешенное мнение 25 экспертов. [c.162]
Эти два уровня отката берут начало из серий чисел, известных как числа Фибоначчи . Эти серии начинаются с числа 1 и прибавляют каждые два стоящих рядом числа вместе (например, 1 + 1=2 1 +2=3 и т. д.). Наиболее часто используются следующие числа Фибоначчи 1, 2, 3, 5, 8, 13, 21, 34, 55 и 89. Очень важно отношение Фибоначчи. Наиболее важное — 38 и 62. Каждое число Фибоначчи составляет приблизительно 62 % следующего, более высокого числа (например, 5/8 = 0,625) отсюда и уровень отката на 62 %. 38 является результатом вычитания 62 из 100 (100-62=38) и отсюда процентный откат на 38 %. Вероятно, это все, что вам надо знать на настоящий момент об этих числах. Они очень популярны среди профессиональных торговцев и широко используются для определения перспектив коррекции [c.29]
ЧИСЛА ФИБОНАЧЧИ - МАТЕМАТИЧЕСКАЯ ОСНОВА ТЕОРИИ ВОЛН [c.348]
Некоторые исследователи пытались найти следы последовательности Фибоначчи в совершенно неожиданных областях. Кто-то измерял среднюю высоту, на которой находится пупок у шестидесяти пяти женщин. Оказалось, что она составляет О, 618 от их общего роста (мы не знаем, мерил ли сей ученый высоту до низа или верха пупка, не говоря уже о том, как вообще можно было додуматься до такого исследования). Тем не менее, следует признать, что числа Фибоначчи встречаются повсюду - буквально в каждой области жизни человека. [c.349]
Прежде всего, если вы посмотрите на примеры (рис. 13.1 и 13.3), то увидите, что в цикличности основных волновых моделей всегда проглядываются числа Фибоначчи. Так, один полный цикл состоит из восьми волн - пяти восходящих и трех нисходящих. Как мы помним, числа 3 и 5 входят в эту последовательность. Дальнейшее разбиение волн на более мелкие дает нам тридцать четыре и сто сорок четыре волны - снова числа Фибоначчи. Однако математическое обоснование теории волн, в основе которой, как уже неоднократно подчеркивалось, лежит числовая последовательность Фибоначчи, конечно, не сводится к простому подсчету волн. Между различными волнами возникают пропорциональные отношения, выраженные числовыми величинами. Наиболее часто встречаются следующие коэффициенты Фибоначчи [c.350]
Количество волн, образующих тенденцию, совпадает с числами Фибоначчи. [c.353]
В примерах, представленных ниже, использованы различные скользящие средние. Их параметры не оптимизированы, ведь среднее скользящее, которое на сегодняшний день является оптимальным, может завтра уже не быть таковым. Наряду с широко распространенными скользящими средними здесь приведены примеры менее употребительных, но основанных на таких инструментах, как числа Фибоначчи. Важно иметь в виду, что в данном контексте нас интересуют не сами скользящие средние, а методы их использования в сочетании со свечами. [c.221]
| Рис. 5.3.1, Числа Фибоначчи в волнах Эллиотта | 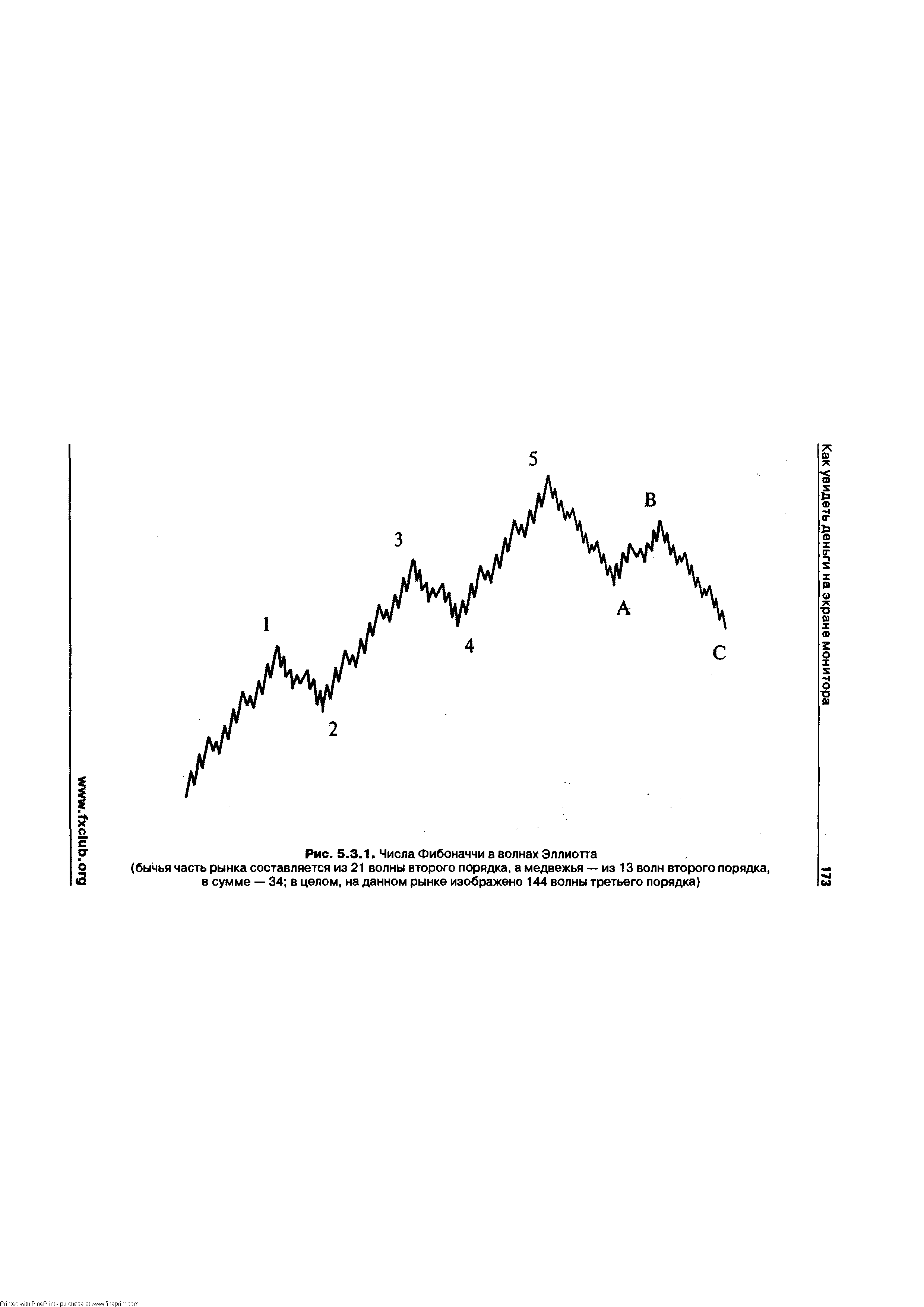 |
Теория, носящая имя Фибоначчи - выдающегося итальянского математика XII-XIII в.в., позволяет использовать числовые коэффициенты (числа Фибоначчи), играющие важную роль в прогнозировании движения рынка. Фибоначчи разработал цифровой ряд (ряд Фибоначчи), состоящий из последовательности чисел 1,2,3,5,8,ВД34 55,89,14 233,377,610,987,1597,2584,4181 итд, [c.64]
Теория, носящая название итальянского математика XII-XIII в. Фибоначчи, позволяет использовать коэффициенты (числа Фибоначчи), играющие важную роль в прогнозировании движения рынка. Фибоначчи разработал цифровой ряд (ряд Фибоначчи), состоящий из последовательности чисел [c.102]
Эти числа связаны между собой рядом любопытных соотношений. Например, каждое число приблизительно в 1,618 раз больше предыдущего, а каждое предыдущее составляет приблизительно 0,618 от следующего. В брошюре Эдварда Добсона Знакомство с числами Фибоначчи (Understanding Fibona i Numbers) эти соотношения [c.247]
Следующее хорошо известное фрактальное измерение лежит между линией и плоскостью, первым и вторым измерением. Названное Уплотнение Сирпиниски в честь другого математика, Вацлава Сирпиниски19, эта размерность имеет численное значение 1.58 (от другого числа Фибоначчи, равного 1.618, это число отличается на тридцать две тысячных). Вы начинаете с равностороннего треугольника и используете половину длины стороны, чтобы образовать первоначальный треугольник. Площадь, которая лежит слева, вмещает три наполовину построенных треугольника. Повторяйте этот процесс до бесконечности, и вы получите форму, которая имеет бесконечное число линий, но не является плоскостью. [c.28]
Фракталы появляются на экране компьютера моделированием, получаемым с помощью итераций. Аккреция -это несистематическая итерация. Одно прибавляется к другому, результат прибавляется к третьему и так далее. Простейшей моделью итерации является последовательность суммирования, известная как числа Фибоначчи. Последовательность начинается с 0 и первые два числа, которые складываются - это 0 и 1. Добавьте 1 к начальнойвеличине - О и получите в результате 1. Добавьте вторую 1 и получите 2. С этого момента, чтобы получить последующее число последовательности, надо стожить два предшествующих числа. Итак, сложите 1 и 2. тогда получите 3. Сложение 2 и 3 дает в результате 5. Добавление 3 к 5 - в результате получим 8. Складывая теперь 5 и 8. получаем 13. Вычисление чисел последовательности по представленным правилам продолжается до бесконечности. Любопытная особенность, присущая этому итеративно-w процессу, заключается в том, что отношение предыдущего числа к последующему стремится к 0.618, вне зависимости от того, какое место в ряду занимают эти числа [c.41]
Летом 1973 года один из моих руководителей произнес убедительную речь, в которой предсказал быстрый корректирующий подъем на фондовом рынке и его завершение к началу осени. На вопрос, какой именно уровень подъема он прогнозирует, руководитель ответил, что ожидает примерно 3/8 или 5/8 от предыдущего спада. Более точного ответа он дать не смог. На вопрос, откуда появились эти числа, мой коллега бойко ответил, что большинство корректирующих подъемов на медвежьем рынке "выдыхается", как правило, на этих уровнях. Еще он вспомнил, что подобные соотношения встретились ему в одном из биржевых бюллетеней и что, если я хочу подробнее узнать о происхождении этих коэффициентов и их скрытом смысле, мне лучше всего обратиться к автору. Так я и поступил. Автор сослался на некоего рыночного аналитика по имени Р. Н. Эллиот и его статью в журнале "Файнэншл Уорлд", напечатанную много лет тому назад. Я немедленно разыскал ее в архивах библиотеки. Статья, посвященная числам Фибоначчи, оказалась не просто захватывающей, но и информативной. К сожалению, в ней не было ответов на многие важные вопросы, и я начал скрупулезно исследовать динамику цен, чтобы выявить точные, объективные методы расчета уровней коррекции. Я стремился сделать эту процедуру полностью механической, чтобы в дальнейшем использовать ее для анализа любого рынка. Результаты моих изысканий изложены ниже. [c.46]
В начале семидесятых годов сразу после знакомства с теорией волн Эллиота я начал искать специалистов в этой области, которые могли бы мне помочь в совершенстве овладеть приемами волнового анализа. К сожалению, я знал только о двух аналитиках, использующих на практике теорию волн Джо Коллинзе из Сент-Луиса и Джеке Фросте из Канады. Они назвали мне ряд инвесторов, экспериментировавших с теорией волн Эллиота и числами Фибоначчи. В частности, мне порекомендовали двух врачей из Флориды, которые, по слухам, хорошо владели предметом. Информация, которую я смог от них получить (вернее, полное отсутствие таковой), и сыграла решающую роль в создании моего собственного подхода к волновому анализу. [c.75]
Элементы числовой последовательности Фибоначчи прочно вплетены в структуру волнового принципа Эллиота, начиная от числа волн и заканчивая величиной коррекции и ценовыми ориентирами. К сожалению, до того, как появился мой полностью механический метод волнового анализа, не было создано ни одной сколько-нибудь объективной методики. В общих чертах, в основе моего подхода — D-волнового анализа — лежат ценовые конфигурации, характеризующиеся определенной последовательностью ценовых максимумов и минимумов. Временной период для каждой такой последовательности определяется числом Фибоначчи. Могут использоваться различные числа из последовательности, но все они должны отвечать одному и тому же требованию. В каждом случае должно накопиться достаточное количество данных для выявления некоего рабочего шаблона. В частности, я выделяю максимальную цену закрытия за 13 дней, такую, что она выше ценовых максимумов всех предшествующих 13 дней. Далее я выделяю первую цену закрытия (после максимальной цены закрытия за 13 дней), которая является минимальной за 8 дней, то есть ниже всех цен закрытия за предыдущие 8 дней. Если эти точки определены, первую волну можно считать завершенной. Вторая волна начинается тогда, когда регистрируется максимальная цена закрытия за 21 день, такая, что она выше всех цен закрытия за предшествующий 21 день. Вторая волна считается завершенной, когда зафиксирована наименьшая цена закрытия за 13 дней, такая, что она ниже всех цен закрытия за предшествующие 13 дней. И, наконец, третья волна начинается, когда реали- [c.75]
Для идентификации волн можно использовать и другие числа Фибоначчи. Последовательность не обязательно должна начинаться с числа 13. Например, числа 21, 34, 55 и так далее позволяют выбрать более долгосрочную перспективу, но уж если выбрано первое чисзк), то все последующие должны подчиняться закономерностям числового ряда, а число дней, в которое регистрируется ценовой минимум, должно составлять 0,618 от числа дней, необходимых для регистрации ценового максимума (см. рис 4.3). [c.77]
Эта книга - о всестороннем и модульном подходе к торговле, который я нахожу разумным и высокоэффективным. Она - о ПРАКТИЧЕСКОМ применении чисел Фибоначчи на инвестиционных рынках. Чтобы успешно реализовывать стратегии, основанные на числах Фибоначчи, нужно иметь солидную базу и структурированный контекст. Книга содержит 15 глав, насыщенных информацией, всеобъемлющий набор Приложений и список рекомендуемой литературы, а также ориентирующую статью в виде Предисловия. Технические приемы с использованием чисел Фибоначчи не раскрываются до ГЛАВЫ 8, пока не будет должным образом проделана работа по укладке фундамента знаний. Если вы решите скакать вперед галопом, надеюсь, вами предварительно сформулирован всесторонний контекст использования мощной техники ведущих индикаторов (leading indi ator te hniques), называемых здесь Уровнями ДиНа-поли. [c.1]
Вы используете 7-дневный осциллятор, 7x5 и 25x5 Смещенные Скользящие Средние, однако 7 и 25 не являются числами Фибоначчи. Почему же вы предпочитаете их [c.137]
Более подробно числа Фибоначчи мы будем рассматривать в главе, посвященной теории волн Эллиота. Однако уже сейчас я хотел бы упомянуть, что этот ряд, универсальность которого явно носит какой-то мистический характер -13,21, 34, 55 и так далее - прекрасно подходит для построения средних скользящих - и не только на дневных графиках, но и на недельных. Число "21", на основе которого строят одно из довольно распространенных средних скользящих (о котором мы уже упоминали, когда рассказывали о дневных графиках), также входит в последовательность Фибоначчи. Тринадцатинедельное среднее скользящее, которое используют, анализируя недельные графики, одинаково хорошо подходит для работы на рынках ценных бумаг и товарных активов. Мы еще вернемся к этой теме и более подробно рассмотрим проблемы использования последовательности Фибоначчи в главе 13 (см. рис. 9.9 а-г). [c.232]
| Рис.9.9в Пример комбинации тринадцати- и тридцатичетырехдневного средних скользящих (числа Фибоначчи). Обратите внимание, насколько уверенно они сдерживали восходящую тенденцию, наметившуюся еще в конце июля. Совсем недавно цены пошли вниз и пересекли обе кривые средних скользящих, указывая на возможный перелом тенденции. Третья кривая, которая находится значительно ниже линии цен, - стосорокачетырехдневное (тридцатинедельное) среднее скользящее. | 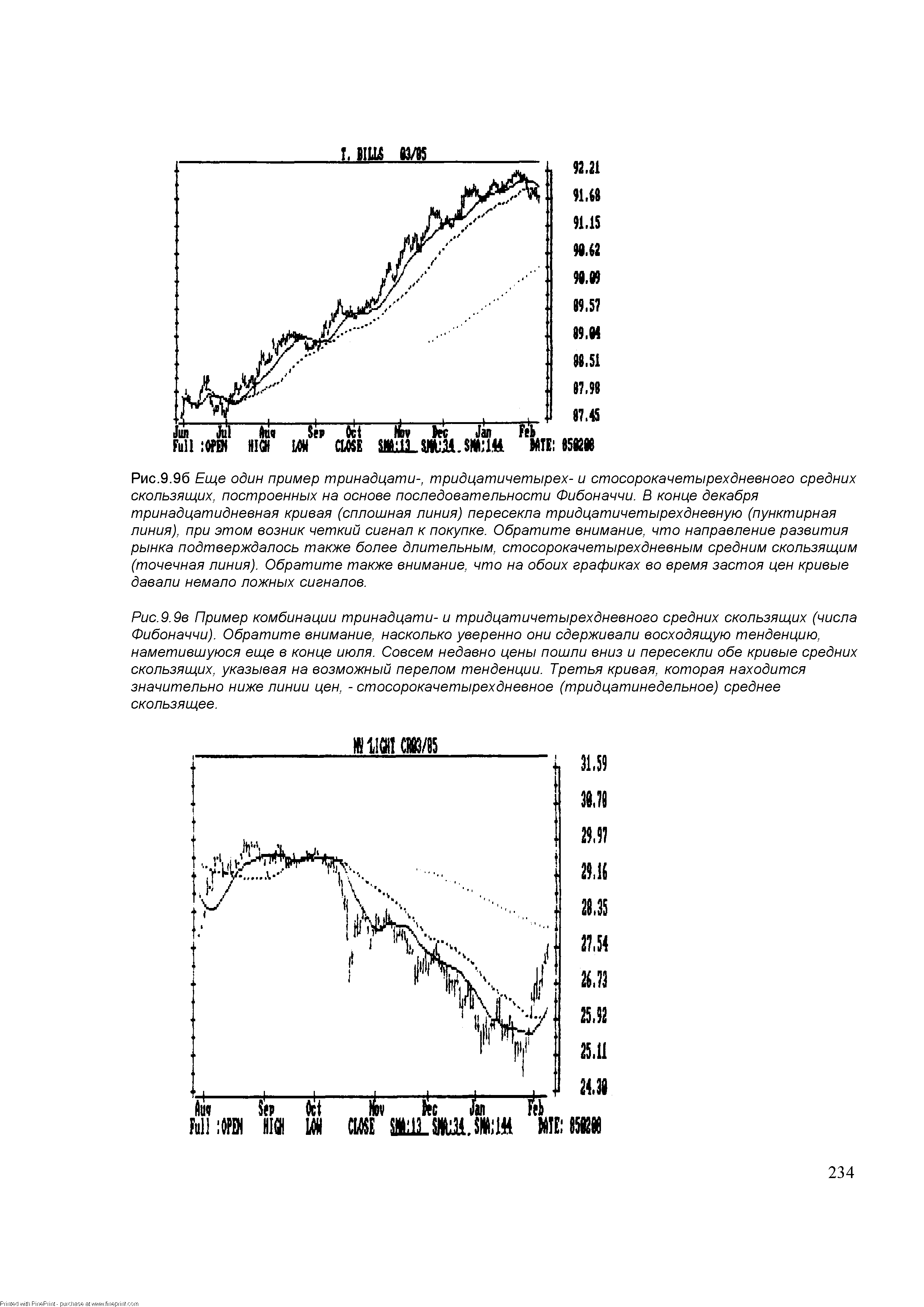 |
| Рис.9.116 Пример тридцатичетырехдневного среднего скользящего (число Фибоначчи), построенного на ценовом графике (вверху). Внизу- пример того же самого среднего скользящего применительно к кривой индикатора ОВ V. | 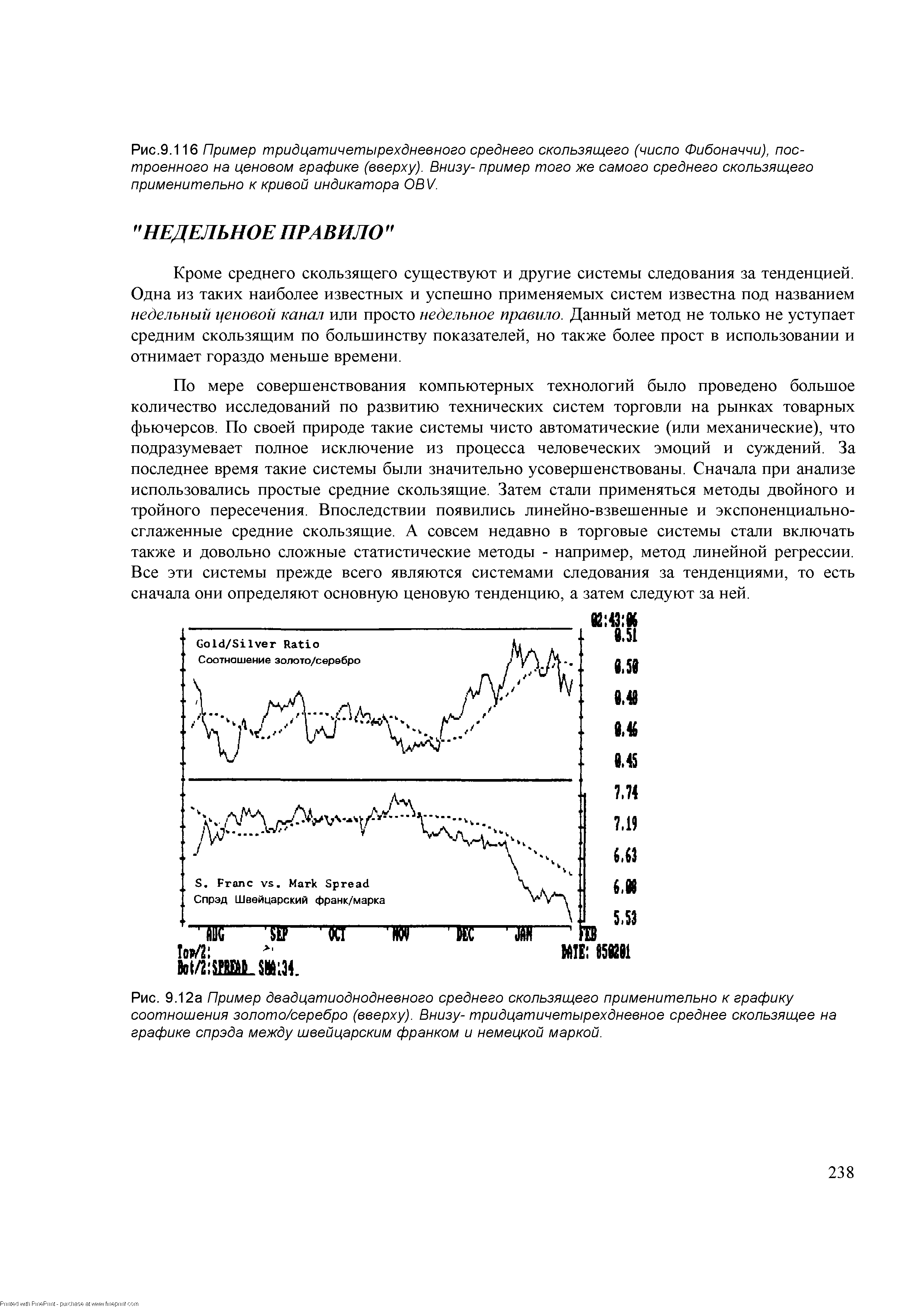 |
Лучшими работами, посвященными теории волн Эллиота и числам Фибоначчи, являются "Избранные работы Р. Эллиота" под редакцией Р. Прехтера и "Принцип волн [c.354]
| Рис. 13. 40 Пример недельного графика. В ходе тринадцатимесячной коррекции вниз (число Фибоначчи ) цены прошли почти 38% расстояния предыдущего роста и затем снова стали подниматься. Обратите внимание на классическую коррекцию А-В-С, в которой волна С подразделяется на пять меньших волн. | 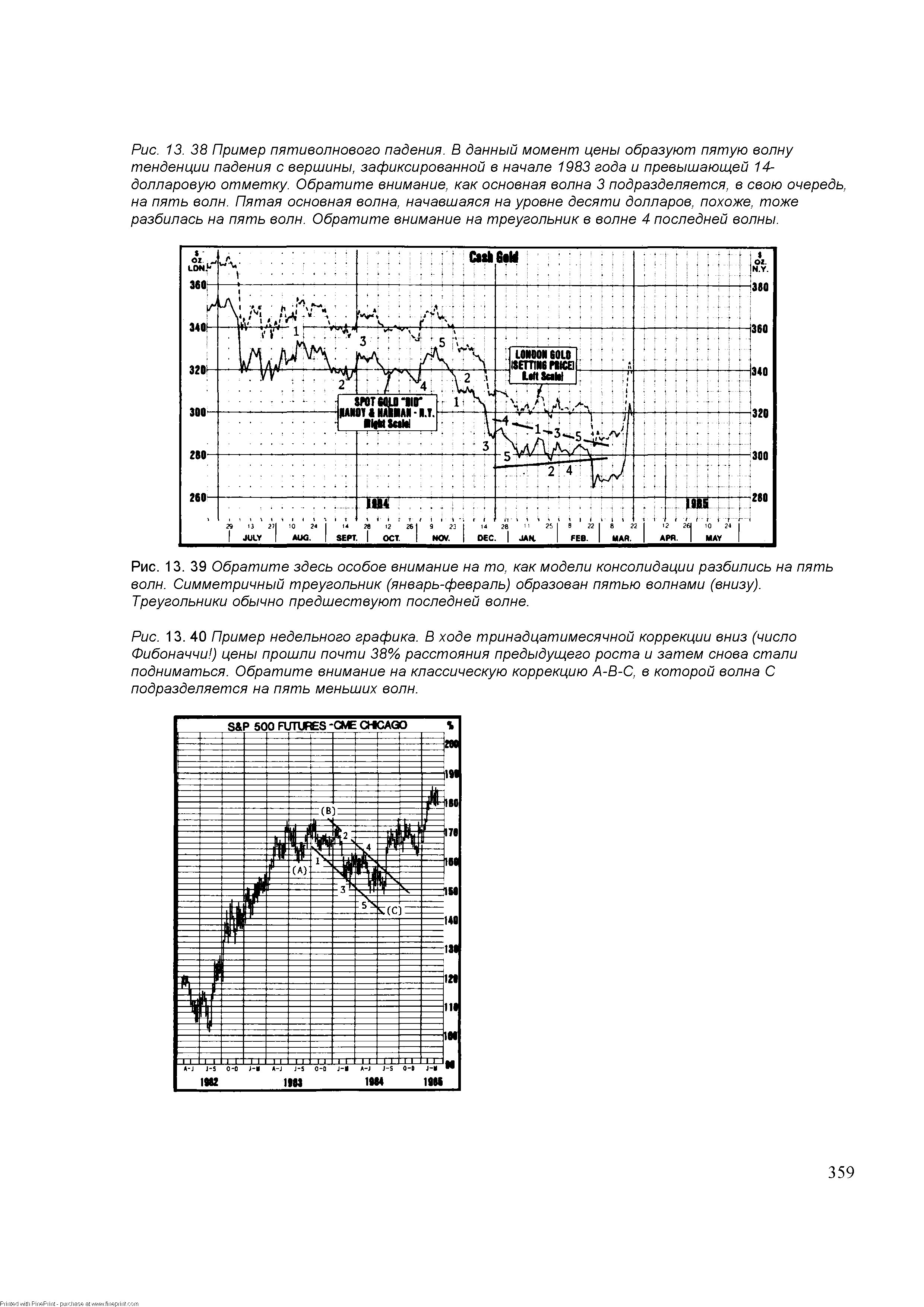 |
Он основан на пропорциях золотого сечения. А само золотое сечение очень тесно связано в математике с числами Фибоначчи. Поэтому-то никто и не удивляется, что подход получил название метода проекций и откатов Фибоначчи. www.fx iub.org [c.180]
Смотреть страницы где упоминается термин Числа Фибоначчи
: [c.4] [c.64] [c.64] [c.102] [c.28] [c.349] [c.355]Смотреть главы в:
Форекс Электронное руководство для успешной торговли на валютном рынке -> Числа Фибоначчи
Технический анализ товарных и финансовых рынков Изд.2 -> Числа Фибоначчи
Мастерство свинг-трейдинга (2005) -- [ c.83 , c.84 , c.85 , c.86 , c.97 , c.102 ]
