Числа Фибоначчи последовательно обнаруживают скрытые уровни поддержки/сопротивления. Используйте данные ключевые уровни для открытия и закрытия прибыльных позиций. Числовые последовательности Фибоначчи дают еще более точные результаты, если они подтверждаются пересечением с другими графическими инструментами. Сами по себе ключевые уровни отката цены не дают возможности определить цель, к которой стремится цена [c.361]
Математической основой теории волн Эллиота являются числа Фибоначчи (см. стр. 206). Не вдаваясь в детали, скажем лишь, что ряд Фибоначчи начинается с единицы, а каждый последующий элемент ряда получается простым суммированием двух предыдущих членов (напр., 0+1=1, 1+1=2, 2+1=3, 3+2=5, 5+3=8, 8+5=13 и т.д.). Полный набор волн любого цикла в теории Эллиота является одним из элементов ряда Фибоначчи. Например на предыдущем графике изображены две основные волны (импульсная и корректирующая), 8 промежуточных волн (последовательность 53 , показанная на первом графике) и 34 малые волны (они отмечены на втором графике). Числа 2, 8 и 34 являются членами ряда Фибоначчи. [c.69]
В дополнение к процентам, описанным выше, существуют и другие популярные среди трейдеров уровни восстановления, а именно 38,2 и 61,8%, в сочетании с упомянутым ранее уровнем 50%. Это числа Фибоначчи, названные по имени европейского математика, изучавшего числовые ряды в XII веке. Он придумал свой ряд, добавляя первое число ко второму, второе к третьему и так далее (1, 1, 2, 3, 5, 8, 13, 21...) Эта последовательность получила название "ряд Фибоначчи" и используется применительно к архитектуре, растениям, человеческому организму и, конечно, рынку. При изучении рядов Фибоначчи обычно используются два процентных значения 61,8 и 38,2%, которые также применяются к восстановлениям на рынке. [c.148]
Я не буду утомлять читателя длинными пассажами о числах Фибоначчи, лежащих в основе окружающего нас мира, а просто сошлюсь на многочисленные учебники и статьи, посвященные описанию этой числовой последовательности и так называемого золотого сечения. Я лишь еще раз подчеркну важность числовой последовательности Фибоначчи, включающей в себя следующие числа 1,2, 3, 5, 8, 13, 21, 34, 55 — и т. д. Каждое последующее число ряда получается путем сложения двух предыдущих чисел. По мере роста номера числа в последовательности отношение предшествующего числа к последующему приближается к 0,618, а отношение последующего числа к предшествующему стремится к 1,618. Такая особенность присуща только членам данной последовательности. [c.46]
После того как вы выбрали формулу для расчета накопления/распределения (я рекомендую ту, которая учитывает цену открытия, а также ценовые разрывы при открытии на восемь и более процентов), необходимо выбрать определенную последовательность временных интервалов. Я рекомендую ряд чисел Фибоначчи, начиная от пяти дней и далее до 13, 21, 34, 55, 89, 144, 233 и 377 дней. Каждый день рассчитывается показатель давления покупателей или продавцов. Сложите все положительные величины (давление покупателей) за выбранное количество дней, а затем — все отрицательные величины (давление продавцов) за тот же период. Затем разделите сумму всех показателей давления покупателей на абсолютную величину суммы всех показателей давления покупателей плюс сумма всех показателей давления продавцов. Полученная величина определяет отношение давления покупателей к общей рыночной активности (давление покупателей плюс давление продавцов), и его можно выразить в процентах, умножив на 100. [c.89]
Еще более важным является индикатор, показывающий скорость изменения данных процентных величин. На своем опыте я убедился, что этот индикатор является наиболее надежным с точки зрения определения наиболее перспективных объектов инвестиций. Скорость изменения рассчитывается просто разделите процентную величину текущего дня на процентную величину X дней тому назад. Обычно я работаю с числами Фибоначчи. Выбрав определенное число, я рассчитываю скорость изменения путем деления сегодняшней величины на величину, отстоящую от сегодняшней, по крайней мере, на четыре уровня Фибоначчи в сторону уменьшения. Допустим, я использую ряд из 89 дней. Чтобы рассчитать скорость изменения, мне нужно сравнить сегодняшнюю величину с величиной 13 дней тому назад — в последовательности Фибоначчи числа возрастают от 13 до 21, 34, 55 и затем до 89. Легко увидеть, что число 13 расположено на четыре уровня ниже, чем число 89. Если бы вы использовали ряд из 144 дней, то нужно было бы сравнивать величину текущего дня с величиной 21 день тому назад если бы вы использовали ряд из 233 дней, то нужно было бы сравнивать величину текущего дня с величиной 34 дня тому назад. Имейте в виду, что это всего лишь рекомендации. Возможно, вы добьетесь лучших результатов, если будете использовать другую числовую последовательность или если для расчета скорости изменения вы выберете другие временные периоды. Но как только период выбран, он должен быть одним и тем же для всех сравниваемых ценных бумаг. Например, если для одного наименования акций выбран 89-дневный период и скорость изменения рассчитывается на основе процентной величины 13 дней назад, тогда те же самые временные отрезки должны использоваться при оценке относительной привлекательности других акций (см. рис. 5.9). [c.90]
Такой способ прогнозирования развития рынка достаточно субъективен и, в силу непостоянства циклических периодов, не может быть проанализирован или проверен статистически. На практике оказывается, что интерпретация циклов достаточно туманна часто там, где предсказывают появление вершины или основания рынка, наблюдается прямо противоположная картина. Такая непредсказуемость вызывала у меня некоторую озабоченность. Поэтому я провел несколько экспериментов, пытаясь применить для определения циклов временную последовательность Фибоначчи, однако полученные результаты, хоть и были чуть лучше, в принципе не содержали ничего необычного. [c.97]
Ряды чисел Фибоначчи имеют больше интересных аспектов, чем многие из нас способны вообразить. В то время как у нас кружится голова от их практически неограниченных возможностей. Для математиков они мороженое со сливочной помадкой, не более того. Рассмотрите эти ряды в том виде, в каком они известны большинству из нас 1, 1,2,3,5,8, 13,21и так далее до бесконечности. Мы получаем ряд, просто складывая вместе последние два числа, начиная с 1,1. Отношения возникают из деления чисел друг на друга различными способами. Например, разделив 13 на 21, мы получим 0,619, в то время как 21 разделенное на 13, дает 1,615. Если перескочить через число и разделить 8 на 21, получится 0,381. Наоборот, 21 разделенное на 8 = 2,625. Чем дальше мы уходим в ряд чисел при делении, тем ближе подходим к достижению точных числовых соотношений Фибоначчи. Однако мы никогда не сумеем до них добраться, поскольку за ними бесконечные последовательности десятичных чисел. В математике это иррациональное число. [c.128]
В главе 13 освещается теория волн Эллиота и числовая последовательность Фибоначчи. Эта теория, первоначально применявшаяся для анализа фондовых индексов, в последние годы стала привлекать повышенное внимание специалистов, работающих на фьючерсных рынках. Принципы Эллиота представляют собой уникальный подход к изучению динамики рынка и при правильном применении позволяют аналитику прогнозировать будущие изменения тенденций с большей степенью уверенности и надежности. [c.10]
Числа 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, которые довольно часто встречаются на страницах этой книги, не случайны. Они входят в так называемую числовую последовательность Фибоначчи, которая служит математической основой теории волн Эллиота. К этой теме мы еще вернемся, а пока посмотрите на примеры (рис. 13.1-13.3), демонстрирующие весьма важную особенность волн. На сколько меньших волн может быть разбита данная волна (три или пять), зависит от направления большей волны, частью которой она является. Так, волны (1), (3) и (5) (рис. 13.2) подразделяются на пять волн каждая, поскольку волна большей степени, волна (I) - восходящая. Поскольку волны (2) и (4) идут в противоположном тенденции направлении, они разбиваются только на три волны меньшей степени. Посмотрите внимательнее на корректирующие волны (а), (Ь), (с) они составляют корректирующую волну (2) (большей степени). Обратите внимание, что две опускающиеся волны - (а) и (с) - подразделяются на пять меньших волн каждая, поскольку идут в том же направлении, что и большая по степени волна (2). Волна (с), наоборот, состоит всего из трех волн, поскольку идет в направлении, противоположном следующей более крупной волне (2). [c.332]
Последовательность Фибоначчи имеет весьма любопытные особенности, не последняя из которых - почти постоянная взаимосвязь между числами. [c.349]
Некоторые исследователи пытались найти следы последовательности Фибоначчи в совершенно неожиданных областях. Кто-то измерял среднюю высоту, на которой находится пупок у шестидесяти пяти женщин. Оказалось, что она составляет О, 618 от их общего роста (мы не знаем, мерил ли сей ученый высоту до низа или верха пупка, не говоря уже о том, как вообще можно было додуматься до такого исследования). Тем не менее, следует признать, что числа Фибоначчи встречаются повсюду - буквально в каждой области жизни человека. [c.349]
В этой главе мы не собираемся подвергать исчерпывающему анализу такие понятия, как "золотые сечения", "золотые прямоугольники" и "логарифмические спирали", не говоря уже о математических основах теории волн и собственно числовой последовательности Фибоначчи. Тем не менее необходимо упомянуть о том, что на основе "золотого коэффициента" можно построить так называемую "логарифмическую спираль", каковая, как полагают, отчасти объясняет универсальный принцип роста, некий закон - общий для всей нашей вселенной. Считается, что спираль сохраняет постоянную форму, в каком бы виде она ни представала. [c.350]
Прежде всего, если вы посмотрите на примеры (рис. 13.1 и 13.3), то увидите, что в цикличности основных волновых моделей всегда проглядываются числа Фибоначчи. Так, один полный цикл состоит из восьми волн - пяти восходящих и трех нисходящих. Как мы помним, числа 3 и 5 входят в эту последовательность. Дальнейшее разбиение волн на более мелкие дает нам тридцать четыре и сто сорок четыре волны - снова числа Фибоначчи. Однако математическое обоснование теории волн, в основе которой, как уже неоднократно подчеркивалось, лежит числовая последовательность Фибоначчи, конечно, не сводится к простому подсчету волн. Между различными волнами возникают пропорциональные отношения, выраженные числовыми величинами. Наиболее часто встречаются следующие коэффициенты Фибоначчи [c.350]
Хотя существуют и другие коэффициенты, те, что мы привели выше, используются чаще всего. Данные коэффициенты помогают определять ценовые ориентиры как для импульсных, так и для корректирующих волн. Однако ценовые ориентиры также можно устанавливать с помощью процентных отношений длины коррекции. Самыми распространенными значениями таких отношений являются 61,8% (обычно округляется до 62%), 38% и 50%. Как вы помните, в главе 4 мы говорили о том, что длина коррекции -величина прогнозируемая и в процентном выражении, как правило, равняется 33%, 50% и 67% от предыдущего движения рынка. Однако, используя числовую последовательность Фибоначчи, процентные значения длины коррекции можно определять еще точнее. Так, при сильной тенденции минимальная длина коррекции обычно составляет около 38%. В случае слабой тенденции длина коррекции, как правило, не превышает 62%. [c.351]
До сих пор мы лишь касались проблемы временного аспекта волнового анализа. Бесспорно, что на рынке существуют также и временные соотношения, в основе которых лежит последовательность Фибоначчи. Однако их тяжелее предсказывать, в связи с чем некоторые последователи Эллиота считают время наименее значительной из трех составляющих теории волн. Временные ориентиры устанавливаются путем прогрессивного отсчета от наиболее значимых экстремумов рынка. На дневном графике подсчитывается количество торговых дней, начиная с какого-нибудь значительного поворотного пункта. При этом [c.351]
Изучение ценовых графиков на рынках ценных бумаг и товарных фьючерсов показывает, что временные соотношения рыночной динамики подчиняются закономерностям числового ряда Фибоначчи. Однако сложность анализа заключается в том, что возможные соотношения такого рода достаточно разнообразны. Временные ориентиры на основе последовательности Фибоначчи можно отсчитывать от вершины до вершины, от вершины до основания, от основания до основания и, наконец, от основания до вершины. По факту соотношения подобного рода устанавливаются легко. Однако в процессе развития тенденции не всегда бывает ясно, какие из них являются существенными. [c.352]
Заканчивая рассмотрение удивительной последовательности чисел Фибоначчи, необходимо добавить, что как аналитический инструмент она нашла свое применение и в других областях технического изучения рынка, например, в анализе средних скользящих. Ничего удивительного в этом нет как известно, наиболее эффективными средними скользящими считаются те, которые "привязаны" к доминирующим циклам рынка. [c.352]
Математической основой теории волн Эллиота является последовательность Фибоначчи. [c.353]
Инструменты, основанные на последовательности Фибоначчи, - веерные линии, дуги и временные зоны [c.355]
| Рис. 13. 45 Временные ориентиры на основе последовательности Фибоначчи устанавливают путем прогрессивного отсчета от важных вершин или оснований рынка. В приведенном примере отсчет произведен от октябрьского пика. Вертикальные линии отмеряют пятый, восьмой, | 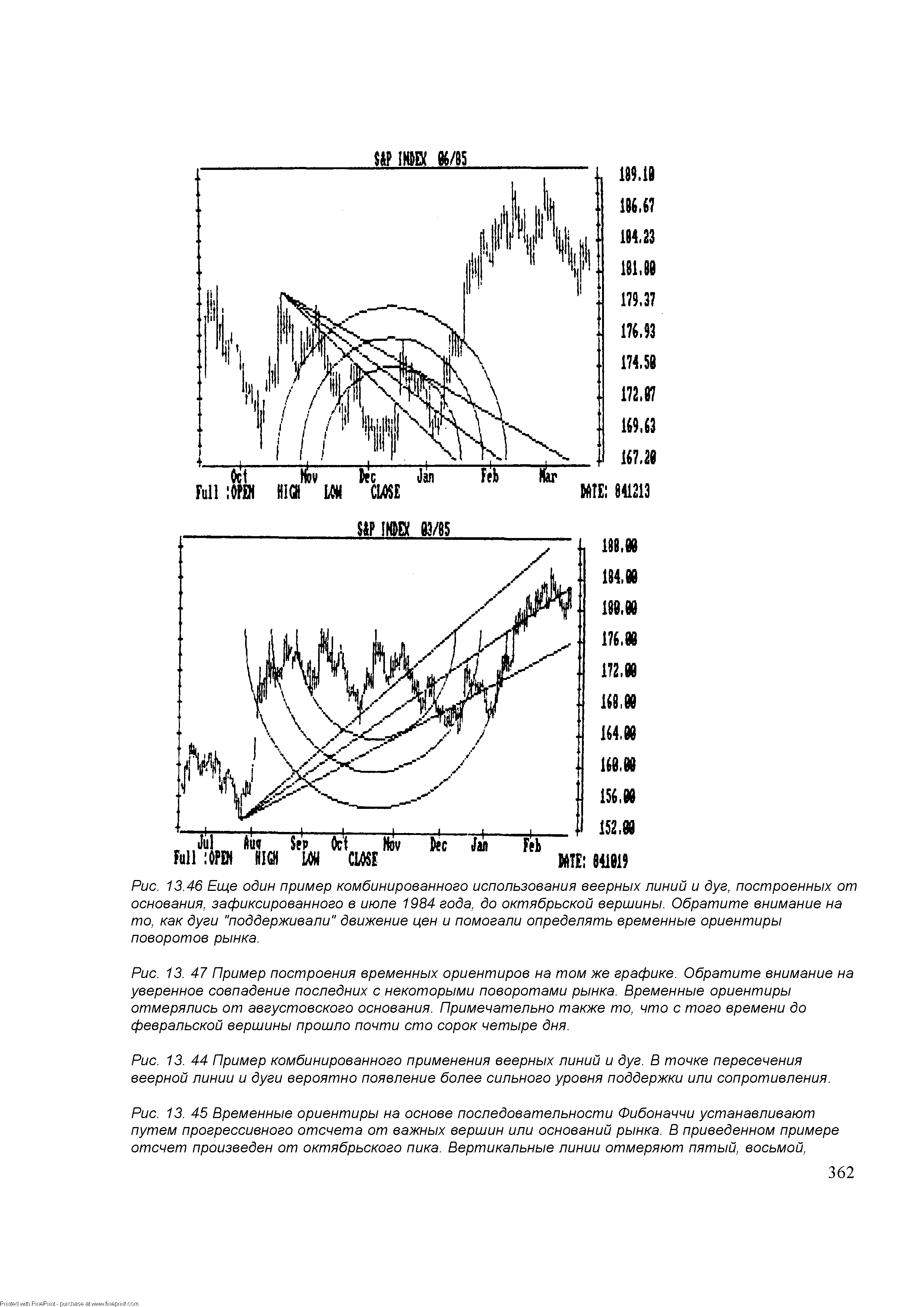 |
Индикаторы циклов и инструменты, основанные на числовой последовательности Фибоначчи, следует использовать как вспомогательные средства, если только они не вызывают у вас особого интереса. При выявлении циклов особенно удобен анализ Фурье, а знание циклов, в свою очередь, помогает повысить точность определения временных периодов для средних скользящих и осцилляторов. Однако следует помнить, что анализ Фурье является достаточно сложной методикой, которую необходимо специально изучать и отрабатывать. Трейдерам, пользующимся механическими торговыми системами, стоит обратить внимание на параболическую систему и систему "направленного движения" Уайлдера. Что касается остальных методов анализа рынка, то я предоставляю читателю самому оценить их возможности. Хочу дать один совет главное, найти инструменты, подходящие именно для вас, которые дают хорошие результаты применительно именно к вашим нуждам. На них и остановитесь. Впрочем, мы еще вернемся к проблеме выбора средств анализа ниже. (См. рис. 15.12- 15.14.) [c.415]
Если длительности трех последовательно расположенных волн попарно не равны, между ними могут наблюдаться соотношения Фибоначчи. [c.221]
Фракталы появляются на экране компьютера моделированием, получаемым с помощью итераций. Аккреция -это несистематическая итерация. Одно прибавляется к другому, результат прибавляется к третьему и так далее. Простейшей моделью итерации является последовательность суммирования, известная как числа Фибоначчи. Последовательность начинается с 0 и первые два числа, которые складываются - это 0 и 1. Добавьте 1 к начальнойвеличине - О и получите в результате 1. Добавьте вторую 1 и получите 2. С этого момента, чтобы получить последующее число последовательности, надо стожить два предшествующих числа. Итак, сложите 1 и 2. тогда получите 3. Сложение 2 и 3 дает в результате 5. Добавление 3 к 5 - в результате получим 8. Складывая теперь 5 и 8. получаем 13. Вычисление чисел последовательности по представленным правилам продолжается до бесконечности. Любопытная особенность, присущая этому итеративно-w процессу, заключается в том, что отношение предыдущего числа к последующему стремится к 0.618, вне зависимости от того, какое место в ряду занимают эти числа [c.41]
Для идентификации волн можно использовать и другие числа Фибоначчи. Последовательность не обязательно должна начинаться с числа 13. Например, числа 21, 34, 55 и так далее позволяют выбрать более долгосрочную перспективу, но уж если выбрано первое чисзк), то все последующие должны подчиняться закономерностям числового ряда, а число дней, в которое регистрируется ценовой минимум, должно составлять 0,618 от числа дней, необходимых для регистрации ценового максимума (см. рис 4.3). [c.77]
Теория, носящая имя Фибоначчи - выдающегося итальянского математика XII-XIII в.в., позволяет использовать числовые коэффициенты (числа Фибоначчи), играющие важную роль в прогнозировании движения рынка. Фибоначчи разработал цифровой ряд (ряд Фибоначчи), состоящий из последовательности чисел 1,2,3,5,8,ВД34 55,89,14 233,377,610,987,1597,2584,4181 итд, [c.64]
Теория, носящая название итальянского математика XII-XIII в. Фибоначчи, позволяет использовать коэффициенты (числа Фибоначчи), играющие важную роль в прогнозировании движения рынка. Фибоначчи разработал цифровой ряд (ряд Фибоначчи), состоящий из последовательности чисел [c.102]
Леонардо Фибоначчи — итальянский математик, родившийся примерно в 1170 году. Считается, что он открыл числовую последовательность, которая теперь называется его именем, изучая пирамиду Хеопса в Гизе. Последовательность Фибоначчи — это числовой ряд, в котором каждый последующий член представляет собой сумму двух предыдущих [c.247]
Наиболее распространенными коэффициентами и коррекциями Фибоначчи, применяемыми эллиотчиками являются 0.236, 0.382, 0.500, 0.618, 0.764, 1.618, 2.618, 4.236, хотя есть и другие, но более редкие. Также следует помнить и саму последовательность Фибоначчи 1,1,2, 3, 5, 8, 13, 21, 34, 55, 89,144, 233,377, 610 и т.д. [c.186]
Приседающий" имеет самый сильный потенциал производителя денег из всех четырех окон Profitunity. Фактически, все движения заканчиваются "приседающим", как самым высоким/низким баром, плюс или минус один бар, того же временного периода. Иными словами, все основные тренды заканчиваются "приседающим", который находится среди одного из трех баров в вершине или основании. Исследование этого, обеспечивает потенциально эффективный способ вхождения в самом начале тренда. Хотя все тренды заканчиваются в "приседающем", тем не менее, "приседающий" не обязательно является окончанием тренда. "Приседающий" появляется весьма часто в середине третьей волны Эллиота, при коррекции согласно последовательности Фибоначчи и пересечении линий Ганна (См. Главу 7). Если в таких обстоятельствах текущий тренд не заканчивается, то такая ситуация имеет склонность становится "контрольным, или мерным, приседающим" (родственно тому, как измеряется разрыв в ценах, гэп), предсказывающим, как далеко еще продлится данное движение. Такой "мерный приседающий" дает нам целевую зону, где мы можем искать другого "приседающего", на котором может закончиться текущая тенденция. [c.76]
О моей неудачной попытке пополнить свои знания в области теории волн Эллиота лучше всего говорят два не связанных друг с другом события. Я пригласил одного из врачей в Висконсин, чтобы он поделился с моими коллегами опытом использования волнового анализа. Когда я приехал в аэропорт, самолет уже приземлился и пассажиры вышли, но моего врача нигде не было. Я позвонил в его офис, чтобы узнать, не опоздал ли он на самолет. Секретарша уверила меня, что он вылетел (она сама его провожала) и что он обязательно найдет меня. В конце концов ко мне подошел человек и спросил "Вы Том " Он заявил, что сразу меня узнал, поскольку в траектории, которую я описывал, блуждая по аэропорту, просматриваются углы Фибоначчи. Я сразу понял, с кем имею дело, и во мне зародилось дурное предчувствие. Оно меня не подвело встреча оказалась абсолютно пустой и безрезультатной. На этом я не сдался, но решил побеседовать со вторым специалистом в области теории волн сначала по телефону, прежде чем приглашать его в Висконсин. Жизнь подтвердила мудрость этого шага. Оказалось, что доктор является страстным поклонником Эллиота и Фибоначчи и что его жизнь полностью основывается на их теориях. В частности, он был три раза женат, у него пять детей, он работает восемь дней подряд, а затем тринадцать дней отдыхает. Я все понял и решил самостоятельно заняться изучением предмета. Я был уверен, что в указанных теориях есть "жемчужное зерно", но мне предстояло найти его самостоятельно. В конце концов последовательность Фибоначчи лежала в основе самых разных явлений начиная от Ед-ипетских пирамид и кончая пересчетом километров в мили. Однако ее роль, равно как и роль теории волн в развитии рынков предстояло еще выяснить. Мой подход к использованию отношений Фибоначчи в расчете величины коррекции уже был описан в главе 2. В этой главе я остановлюсь на применении разработанных мной методик волнового анализа. [c.75]
Элементы числовой последовательности Фибоначчи прочно вплетены в структуру волнового принципа Эллиота, начиная от числа волн и заканчивая величиной коррекции и ценовыми ориентирами. К сожалению, до того, как появился мой полностью механический метод волнового анализа, не было создано ни одной сколько-нибудь объективной методики. В общих чертах, в основе моего подхода — D-волнового анализа — лежат ценовые конфигурации, характеризующиеся определенной последовательностью ценовых максимумов и минимумов. Временной период для каждой такой последовательности определяется числом Фибоначчи. Могут использоваться различные числа из последовательности, но все они должны отвечать одному и тому же требованию. В каждом случае должно накопиться достаточное количество данных для выявления некоего рабочего шаблона. В частности, я выделяю максимальную цену закрытия за 13 дней, такую, что она выше ценовых максимумов всех предшествующих 13 дней. Далее я выделяю первую цену закрытия (после максимальной цены закрытия за 13 дней), которая является минимальной за 8 дней, то есть ниже всех цен закрытия за предыдущие 8 дней. Если эти точки определены, первую волну можно считать завершенной. Вторая волна начинается тогда, когда регистрируется максимальная цена закрытия за 21 день, такая, что она выше всех цен закрытия за предшествующий 21 день. Вторая волна считается завершенной, когда зафиксирована наименьшая цена закрытия за 13 дней, такая, что она ниже всех цен закрытия за предшествующие 13 дней. И, наконец, третья волна начинается, когда реали- [c.75]
Правда, новая техника торговли не работала по-настоящему хорошо, пока мой третий наставник не рассказал об итальянском математике по имени Фибоначчи. Номер третий также был человеком эксцентричным. Но он не умел обращаться с компьютером и не слыл затворником. Бесспорно, этот чудак самый великолепный трейдер, которого я когда-либо встречал. Он уверенно использовал аналитические методы, и я воочию видел, как он ловил максимумы, минимумы, промежуточные максимумы подъемов, промежуточные минимумы понижений. Все, что угодно Его стиль торговли полностью отрицал все понятия рациональности, и он проделывал это прямо у меня на глазах Только после того, как однажды он раскрыл мне свои секреты, я понял, его методы не имели ничего общего с последовательной, прибыльной торговлей. Когда опыт и время разрушили в моих глазах образ еще одного героя, я увидел, что он идет от богатства к обноскам, неплатежеспособности, долгам. Похоже, что в Священном Граале (Holy Grail) нужно было залатать еще немало дырок. Только на основе собственного опыта через много, много лет мне удалось с большим трудом прийти к заключениям, из нитей которых я соткал следующее полотно. [c.10]
Более подробно числа Фибоначчи мы будем рассматривать в главе, посвященной теории волн Эллиота. Однако уже сейчас я хотел бы упомянуть, что этот ряд, универсальность которого явно носит какой-то мистический характер -13,21, 34, 55 и так далее - прекрасно подходит для построения средних скользящих - и не только на дневных графиках, но и на недельных. Число "21", на основе которого строят одно из довольно распространенных средних скользящих (о котором мы уже упоминали, когда рассказывали о дневных графиках), также входит в последовательность Фибоначчи. Тринадцатинедельное среднее скользящее, которое используют, анализируя недельные графики, одинаково хорошо подходит для работы на рынках ценных бумаг и товарных активов. Мы еще вернемся к этой теме и более подробно рассмотрим проблемы использования последовательности Фибоначчи в главе 13 (см. рис. 9.9 а-г). [c.232]
Многие туристы, побывавшие в итальянском городе Пиза, обязательно приходят полюбоваться на знаменитую "падающую" башню, которую построил архитектор Бонанна. Башня действительно стоит под углом, то есть не перпендикулярно к земной поверхности. Что же общего у пизанской башни с рынком ценных бумаг, в целом, и теорией волн Эллиота, в частности Почти ничего. Однако недалеко от башни находится небольшая статуя, на которую редко обращают внимание туристы. Речь идет о памятнике знаменитому итальянскому математику Леонардо Фибоначчи. Что общего между математиком, жившим в тринадцатом веке, с одной стороны, и теорией волн Эллиота и динамикой рынка ценных бумаг, с другой Очень много общего. Как признал сам Эллиот в своем "Законе природы", математической основой его теории стала последовательность чисел, которую открыл (или, [c.348]
Последовательность Фибоначчи содержит и другие любопытные соотношения, или коэффициенты, но те, которые мы только что привели - самые важные и известные. Как мы уже подчеркнули выше, на самом деле Фибоначчи не является первооткрывателем своей последовательности. Дело в том, что коэффициент 1,618 или 0,618 был известен еще древнегреческим и древнеегипетским математикам, которые называли его "золотым коэффициентом" или "золотым сечением". Его следы мы находим в музыке, изобразительном искусстве, архитектуре и биологии. Греки использовали принцип "золотого сечения" при строительстве Парфенона, египтяне - Великой пирамиды в Гизе. Свойства "золотого коэффициента" были хорошо известны Пифагору, Платону и Леонардо-да-Винчи. [c.349]
Нет, пожалуй, такой теории, которая содержала бы ответы на все вопросы. Лично я в течение уже многих лет успешно использую теорию волн Эллиота и последовательность чисел Фибоначчи. Мой опыт не позволяет мне присоединиться к тем, кто утверждает, что любое движение товарого рынка может быть в точности объяснено с помощью данной теории. Иногда волновая структура наглядно показывает возможный ход рынка, иногда -нет. Когда я вижу четкую и ясную конфигурацию волн, я пользуюсть ею, когда сомневаюсь, то обращаюсь к другим средствам анализа. Когда ход рынка неявен, а его пытаются насильно загнать в рамки теории Эллиота, полностью игнорируя при этом другие методы технического анализа, то это можно назвать самым настоящим злоупотреблением - метода, который в иных условиях может оказаться довольно полезным. Увы, злоупотребления часто приводят к печальным последствиям. Гораздо мудрее относиться к волнам Эллиота лишь как к частичному ответу на вечную загадку рыночного прогноза. Эффективность теории волн только повышается, когда ее применяют в сочетании с другими аналитическими инструментами, рассмотренными в нашей книге, а шансы на успех возрастают. [c.354]
Волновой анализ Эллиота (Elliott Wave Analysis) -один из подходов к анализу рынка, основанный на гипотезе о повторяемости волновых моделей и числовой последовательности Фибоначчи. Идеальная волновая модель Эллиота состоит из пятиволнового роста, за которым следует трехволновое падение. Каждый следующий член последовательности Фибоначчи образуется путем сложения двух предыдущих (1,2,3, 5,8,13,21,34, 55,89,144...). Отношение любого члена последовательности Фибоначчи к последующему равно 0,62, что представляет собой распространенное значение длины коррекции Фибоначчи. Дополнение этого числа до единицы, то есть 0,38, также используется как уровень коррекции Фибоначчи. Отношение любого члена последовательности Фибоначчи к предыдущему - 1,62 - применяется для расчета ценовых ориентиров Фибоначчи. Волновой анализ Эллиота включает в себя три элемента модель (идентификация волны), коэффициенты (проекции и коэффициенты Фибоначчи) и время. Временные ориентиры Фибоначчи находят, отложив от важного ценового пика или впадины временной отрезок (в днях, неделях, месяцах или годах), величина которого равна одному из членов последовательности Фибоначчи. [c.293]
Смотреть страницы где упоминается термин Фибоначчи последовательность
: [c.528] [c.549] [c.127] [c.234] [c.235] [c.349] [c.349] [c.355] [c.355] [c.355] [c.396]Секреты биржевой торговли Издание 3 (2006) -- [ c.0 ]
