По каждому году оцениваются степень риска элемента денежного потока конкретного проекта и сумма его безрискового эквивалента Et. Например, на третий год реализации проекта ожидается денежный поток в 1000 тыс. руб., уровень риска оценивается как средний. Лицо, принимающее решение, считает, что безрисковый эквивалент Et должен составить 600 тыс. руб. [c.171]
Для того чтобы оба рассмотренных метода привели к одному и тому же значению NPV, необходимо, чтобы дисконтированные элементы потока быть равны между собой. Из этого положения следует ряд интересных выводов, в том числе следующий при неизменных значениях безрисковой доходности и ставки дисконтирования, учитывающей риск, риск с течением времени возрастает, что отражается в уменьшении безрискового эквивалента. [c.171]
| Рис. 2.1. Математическое ожидание, ожидаемая полезность, безрисковый эквивалент и премия за риск | 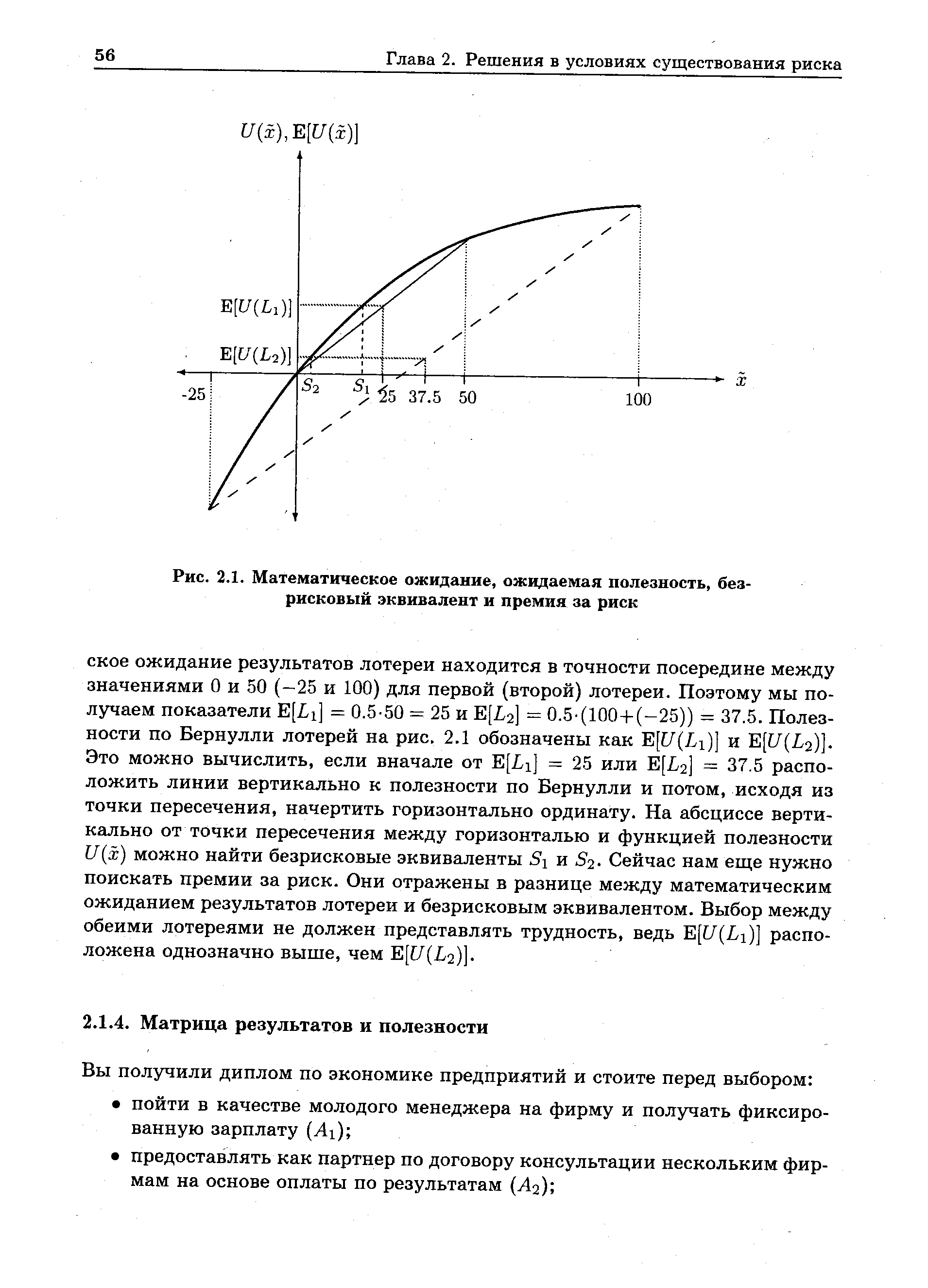 |
Обратной функцией к In У является eY. Таким образом, для безрискового эквивалента мы получаем [c.65]
Является ли эта полученная сегодняшняя стоимость справедливой ценой или мы здесь имеем дело с искаженным вариантом Для ответа на этот вопрос мы рассчитаем сегодняшнюю стоимость с помощью безрискового эквивалента. Для этого мы должны исключить Ро в правой части (4.82). Так как [c.216]
Для анализа инвестиционных проектов в условиях риска применяют метод безрискового эквивалента или метод скорректированного на риск коэффициента дисконтирования. [c.403]
Безрисковый эквивалент я премия за риск [c.655]
Безрисковым эквивалентом случайного выигрыша называется гарантированный выигрыш, приводящий к полезности богатства, равной ожидаемой полезности случайного выигрыша. Используя обозначения G для случайного выигрыша и g — для его безрискового эквивалента, мы можем это определение выразить равенством [c.656]
Если APA(w) — возрастающая функция, то с увеличением богатства безрисковый эквивалент случайного выигрыша убывает, и наоборот. [c.660]
Функция полезности u(w)= -4w, к которой мы много раз обращались, имеет постоянную относительную меру Эрроу — Пратта АРЯ= 0.5. Как и для любой другой функции полезности с постоянной относительной мерой Эрроу — Пратта, для нее абсолютная мера Эрроу — Пратта убывает (APA(w) = a/w). Для индивида с такой функцией полезности безрисковый эквивалент с ростом богатства возрастает. Именно поэтому купец в рассмотренном примере смог договориться со страховщиком, имеющим ту же самую функцию полезности бедный купец за уклонение [c.661]
Иными словами, процентный доход по надежному займу должен быть безрисковым эквивалентом случайного выигрыша — дохода по ненадежному займу. [c.662]
Безрисковый эквивалент 2 656, 658, 732 Блага [c.756]
Логика построения безрисковых эквивалентов в значительной степени базируется на идеях теории полезности в том смысле, что, рассматривая поэлементно денежный поток рискового проекта, инвестор в отношении его пытается оценить, какая гарантированная, т.е. безрисковая, сумма денег потребуется ему, чтобы быть индифферентным к выбору между этой суммой и ожидаемой, т.е. рисковой, величиной k-ro элемента потока. [c.109]
Очевидно, что ожидаемый доход в случае А равен 500 тыс. долл., в случае В гарантированный доход равен 350 тыс. долл. Теперь задайте себе вопрос, какая гарантированная сумма сделает вас индифферентным к выбору между последней суммой денег и рисковым ожидаемым доходом в 500 тыс. долл. Для подавляющего большинства людей эта сумма(350 тыс. долл.), как раз и является безрисковым эквивалентом, что гораздо меньше 500 тыс. долл. Поскольку люди по-разному относятся к риску, величина безрискового эквивалента является субъективной и переменной, причем чем меньше ее значение по сравнению с исходной суммой, тем большее неприятие риска демонстрирует лицо, принимающее это решение. Графически отношение к риску выражается с помощью кривых безразличия (индифферентности). [c.109]
Поскольку 7 тыс. долл. - это рисковая сумма, можно найти ее безрисковый эквивалент, который численно равен абсциссе точки М, являющейся точкой пересечения кривой безразличия и прямой, исходящей из N и параллельной оси абсцисс. [c.113]
Предположим, что безрисковый эквивалент ожидаемого дохода в 7 тыс. долл. равен 6,2 тыс. долл. Поскольку ожидаемые поступления представляют собой срочный аннуитет, для оценки проекта можно воспользоваться дисконтирующим множителем FM4(r%, n). [c.113]
Если риск учитывается, то в расчет принимается безрисковый эквивалент, a NPV будет иметь следующее значение [c.113]
| Рис. 12.4. Нахождение безрискового эквивалента графическим методом |  |
Как же на практике находят безрисковые эквиваленты Существуют различные способы. Например, можно попытаться оценить вероятность появления заданной величины денежного поступления для каждого года и каждого проекта. После этого составляются новые проекты на основе откорректированных с помощью понижающих коэффициентов денежных потоков и для них рассчитываются NPV (понижающий коэффициент представляет собой вероятность появления рассматриваемого денежного поступления). По сути, откорректированный поток и представляет собой поток из безрисковых эквивалентов. Предпочтение отдается про- [c.114]
Для того чтйбы мы могли определить сегодняшнюю стоимость инвестиционного проекта из задания 4.4.1, в контексте САРМ существуют две разные возможности. Или ожидаемые возвратные потоки дисконтируются на основе скорректированной с учетом риска ставки процента, или безрисковый эквивалент дисконтируется на основе ставки процента по безрисковому активу. [c.214]
В тех случаях, когда математическое ожидание выигрыша равно нулю, безрисковый эквивалент для рискофоба отрицателен, для рискофила — положителен, для рисконейтрала — равен нулю. [c.656]
Из этого определения следует, что цена продавца равна безрисковому эквиваленту выигрыша (Ра = уе), и поэтому для рискофоба Ра < М[У]. Разность между ожидаемым выигрышем и ценой продавца получила название рисковой премии, или премии за риск (по оценке продавца) [c.657]
Введем обозначение G = Y - Рь для чистого выигрыша. Из приведенного определения следует, что цена покупателя обращает в нуль безрисковый эквивалент чистого выигрыша (ge = 0), так что для рискофоба M[G] = М[У] - Р >0. Превышение ожидаемого выигрыша над ценой покупателя также получило название рисковой премии (на сей раз — по оценке покупателя) [c.657]
Прежде всего заметим, что он захочет купить ценные бумаги только в том случае, если математическое ожидание чистого выигрыша положительно. Если бы оно было отрицательно или равно нулю, безрисковый эквивалент (для рискофоба он меньше математического ожидания) был бы заведомо отрицательным, и приобретение актива в любом положительном количестве вело бы к потере полезности. С другой стороны, если чистый выигрыш при любом исходе принимает неотрицательные значения, то полезность заведомо тем больше, чем большее количество актива приобретет индивид, и он захочет вложить в его покупку все свое богатство. [c.658]
Итак, будем считать, что M[G] > 0, и, следовательно, при любом положительном х выполняется соотношение M[Gx] = M[G] > 0. Кроме того, примем, что среди возможных значений чистого выигрыша gl имеются отрицательные. При малом х кривизна функции полезности, как отмечалось выше, сказывается слабо, и безрисковый эквивалент также положителен, так что покупка бумаг повысит полезность индивида. С увеличением х эффект рискофобии будет сказываться все заметнее, и при достаточно больших значениях х безрисковый эквивалент выигрыша за счет влияния отрицательных выигрышей начнет убывать, а следовательно, начнет убывать и полезность. Иными словами, можно полагать, что при некотором значении х не склонный к риску индивид получит максимальную полезность. Именно это количество бумаг он и захочет приобрести. [c.658]
Но для кредитора-рискофоба при такой ставке безрисковый эквивалент окажется меньше i-l, и чтобы заинтересовать его в сделке, ставка должна быть повышена, и тем значительнее, чем больше его стремление избежать риска. Если его устраивает процентная ставка г, то разность г- г0 представляет собой рисковую премию в составе процентной ставки. [c.663]
Безрисковый эквивалент (risk-free equivalent) — гарантированный выигрыш, приводящий к полезности богатства, равной математическому ожиданию полезности богатства при случайном выигрыше [c.732]
В данной формуле мы, чтобы учесть риск, скорректировали числитель, а дисконтирование проводим по безрисковой ставке. Числитель в (2.19) иногда называют безрисковым эквивалентом ( ertainty equivalent) будущим платежам. [c.74]
Очевидно, что величина безрискового эквивалента зависит от двух факторов степени выпуклости кривой безразличия и рисковости ожидаемого дохода. Так, если в нашем примере с опционом возможные значения дохода равны 4,8 тыс. руб. и 7,2 тыс. руб., т. е. при неизменившейся величине ожидаемого дохода риск его получения увеличился (на графике этой ситуации соответствует прямая D), безрисковый эквивалент шести тысяч рублей будет меньше и составит величину Р. [c.112]
С некоторой долей условности можно считать, что в теоретическом плане метод RADR более оправдан, поскольку введение поправки на риск автоматически приводит к принятию безусловно обоснованной предпосылки о возрастании риска с течением времени. Конечно, эта предпосылка может быть учтена и при расчете безрисковых эквивалентов. По свидетельству западных специалистов, из рассмотренных методов учета риска метод RADR пользуется большей популярностью. Обычно называют две причины а) менеджеры и аналитики предпочитают работать с относительными показателями, в частности с показателями доходности б) ввести поправку к коэффициенту дисконтирования гораздо легче, нежели рассчитывать безрисковые эквиваленты, тем более, что в любом случае решение является субъективным. Во многих компаниях для удобства вводят специальную шкалу, в которой указаны значения коэффициента дисконтирования в зависимости от того, какой уровень риска может быть приписан данному проекту, например ниже среднего, средний, выше среднего и весьма высокий. Как градация шкалы, так и значения коэффициента дисконтирования периодически пересматриваются и, кроме того, могут специфицироваться по видам инвестиций, подразделениям, регионам и другим классификационным признакам. [c.117]
Смотреть страницы где упоминается термин Безрисковый эквивалент
: [c.209] [c.55] [c.56] [c.65] [c.294] [c.656] [c.4] [c.74] [c.110] [c.112] [c.401]50 лекций по микроэкономике Том 2 (2000) -- [ c.2 , c.656 , c.658 , c.732 ]
