| Рис.1. Классификация методов формализации экономических задач с учетом риска и неопределенности на основе диаграммы Эйлера-Венна. | 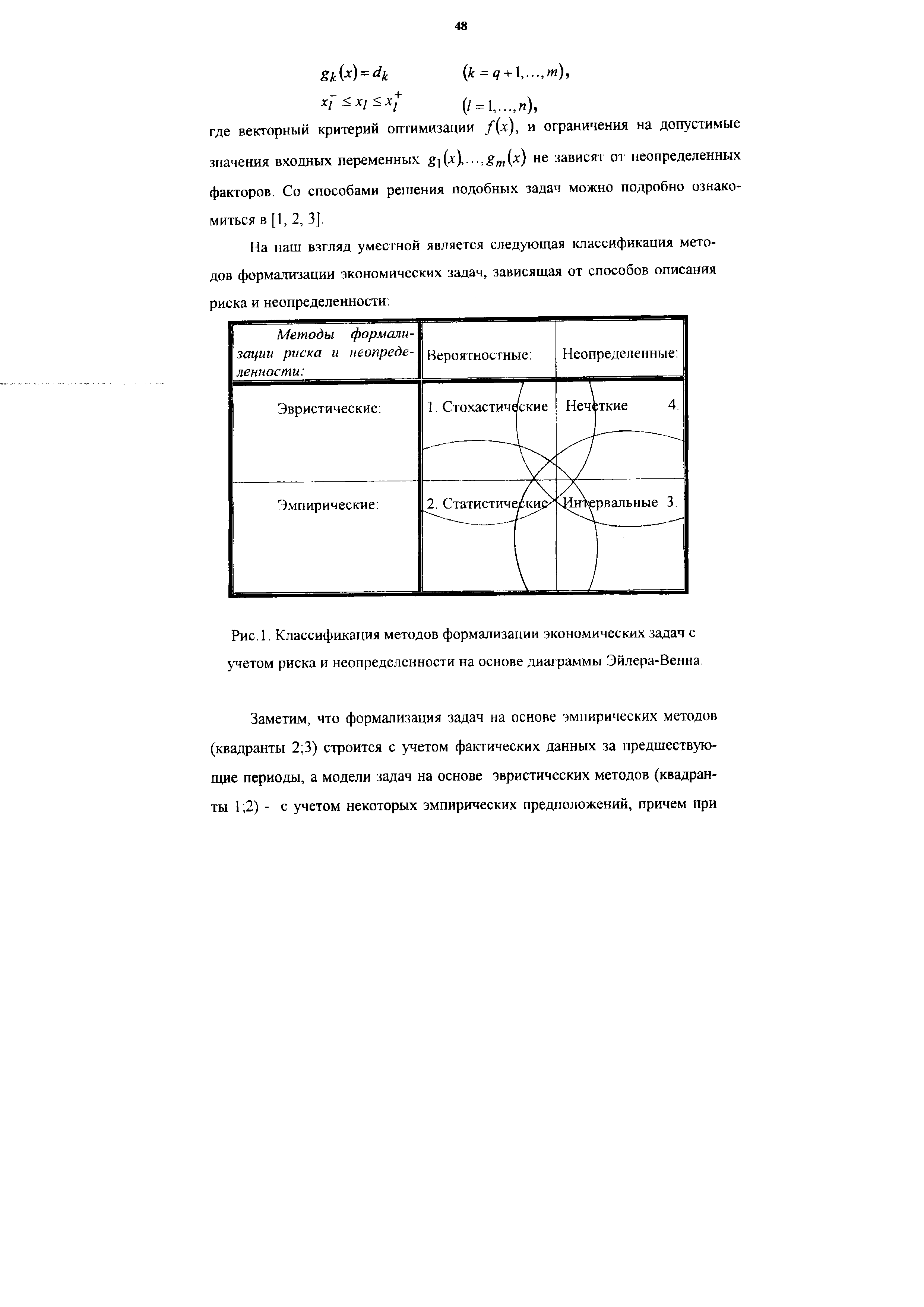 |
Таким образом, инновации можно представить в виде диаграммы Эйлера-Венна, где пересекающимися множествами являются множества [c.66]
Объясните, что означают на диаграмме Эйлера-Венна участки с разной штриховкой [c.85]
| Фиг. 1. Диаграмма Венна для теорем в базе данных. | 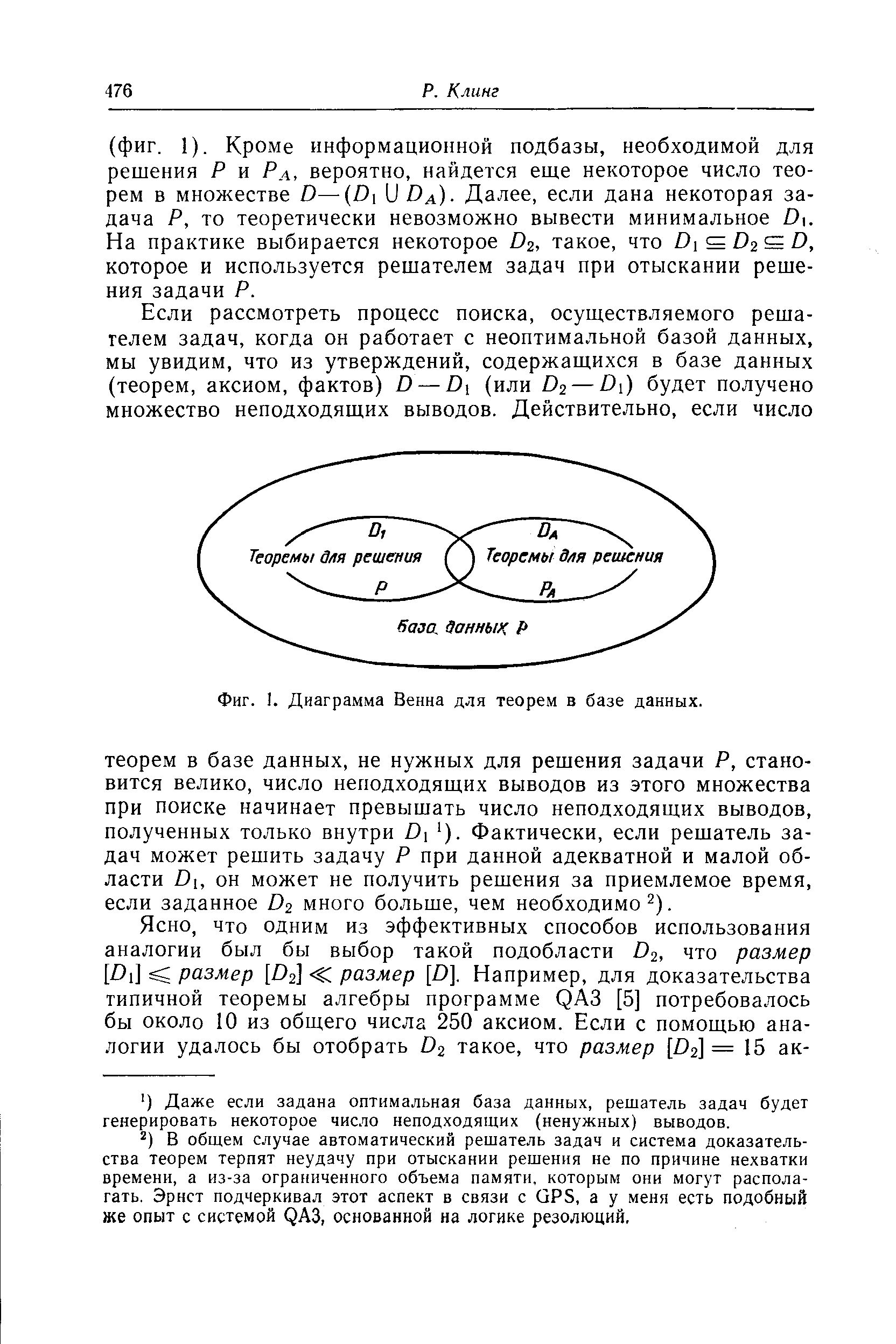 |
| Фиг. 2. Диаграммы Венна, характеризующие отношения между формулировками теорем Т, ТА и базой данных D. |  |
Контекстная диаграмма - самый верхний процесс (ТОР-уро-вень) декомпозиции системы, который отражает общие представления о системе. В контекстной диаграмме есть 1 процесс, с которым связаны внешние сущности. [c.333]
Рассмотрим вначале диаграмму Венна на рис. 30. Рисунок показывает, что вероятности события А и/или Л2 удовлетворяют условиям [c.174]
На практике приходится использовать несколько различных типов моделей для описания всех требуемых аспектов функциональности системы. А поскольку каждая модель содержит информацию определенного типа, а каждая технология моделирования использует свою собственную семантику, то информация в одной модели может быть отделена от информации в другой модели. Но с другой стороны, одна и та же информация может появляться в нескольких моделях. В последнем случае очень важно быть уверенным, что если информации меняется в одной из моделей, то это изменение отражается и во всех остальных моделях, в которых эта информация встречается. В идеальном варианте это может происходить автоматически с помощью сопряжения (интеграции) моделирующих инструментов. Если же это по каким-то причинам не может быть организовано, то необходимо проявлять исключительную педантичность и аккуратность, чтобы удостовериться в том, что любое изменение информации в одном месте идентично отражается в других связанных моделях. Диаграмма Венна (рис. 6.4) иллюстрирует, что некоторые модели могут быть представлены в виде отдельных островков информации, в то время как другие модели могут иметь общую информацию, возможно представленную в разных формах. Диаграмма также демонстрирует тот факт, что часть информации о системе не отражена ни в одной из моделей. [c.134]
ВЕННА ДИАГРАММЫ [Venn diagrams] — способ графического изображения множеств. Конечное множество может быть условно представлено как совокупность точек, окруженных подходящей фигурой (напр., кругом, квадратом или треугольником). Таким об- [c.44]
Совершенная мультиколлинеарность является скорее теоретическим примером. Реальна же ситуация, когда между объясняющими переменными существует довольно сильная корреляционная зависимость, а не строгая функциональная. Такая зависимость называется несовершенной мулътиколлинеарностъю. Она характеризуется высоким коэффициентом корреляции р между соответствующими объясняющими переменными. Причем, если значение р по абсолютной величине близко к единице, то говорят о почти совершенной мульти-коллинеарности. В любом случае мультиколлинеарность затрудняет разделение влияния объясняющих факторов на поведение зависимой переменной и делает оценки коэффициентов регрессии ненадежными. Данный вывод наглядно подтверждается с помощью диаграммы Вен-на (рис. 10.1). [c.246]
