Позиционная форма представляется деревом игры, кото- [c.20]
Мы имеем дерево игры с конечным множеством вершин [c.86]
Начинаем с конца дерева игры и определяем равновесия [c.102]
Кроме того, удобно представить ситуацию как игру в развернутой форме. Можно изобразить последовательность ходов и выигрыши игроков с помощью следующего дерева игры [c.47]
Рассмотрим сначала ситуацию, когда покупатель знает качество товара. Тогда дерево игры в этой ситуации имеет вид, изображенный на Рис. 93. [c.464]
Для поиска равновесия этой игры используем обратную индукцию. Рассмотрим решение покупателя. Если v(s)>p, то покупатель покупает, если v(s]
Формально можем рассматривать эту модель как динамическую байесовскую игру и найти в ней совершенное байесовское равновесие — совокупность согласованных стратегий и ожиданий. В игре нулевой ход делает природа — она выбирает тип продавца. Дальше при каждом s дерево игры совпадает с деревом, изображенным на Рис. 93. [c.465]
Эта модель приложима, например, к ситуации, когда в новой отрасли лидирующая фирма выбирает размер строящегося завода (мощность) и решает работать на полную мощность . Считается, что она хорошо описывает рыночную ситуацию в случае, когда фирма-лидер, занимает значительную долю рынка. Так или иначе, ситуации, представленные в модели не столь и редки на реальных рынках. С точки зрения теории игр модель Штакельберга представляет собой динамическую игру с совершенной информацией, в которой лидер делает ход первым. Дерево игры изображено на Рис. 113. [c.540]
Схема игры представлена на Рис. 124. Это не полное дерево игры, а только условное описание последовательности ходов. [c.565]
Данную игру удобно представить в виде диаграммы, изображающей дерево игры (см. Рис. [c.653]
Чтобы было более понятно, какой выбор стоит перед пилотом, удобно частично свернуть дерево игры, учитывая то, что действия террориста в Нью-Йорке известны. Полученная усеченная (редуцированная) игра показана на Рис. 156. [c.654]
Первые два пункта здесь соответствуют описанию дерева игры. [c.655]
Нарисуйте дерево игры при п = 3. Опишите множество стратегий каждого из игроков. [c.663]
Дополнительно следует потребовать, чтобы множество возможных действий во всех вершинах одного и того же информационного множества были одинаковыми. В противном случае игрок мог бы по тому, какие альтернативы ему доступны, определить, в какой именно вершине он находится. Дерево игры, представленное на Рис. 163 удовлетворяет этому требованию — ив вершине , и в вершине 2-й игрок выбирает между IBM и Мае. [c.665]
Этой нормальной форме соответствует дерево игры, представленное на Рис. 166. Как видим, при таком двойном переводе частично потеряна информация о структуре игры и мы получили другую игру в развернутой форме. Очевидно, что принципиально разным играм может соответствовать одна и та же нормальная форма. [c.666]
Таким образом, нормальная форма игры не является в общем случае адекватной для описания динамических игр. С помощью нее можно представлять корректно только статические игры. Если операцию двойного перевода из развернутой формы в нормальную и обратно осуществить со статической игрой, представленной на Рис. 163, то дерево игры не поменяется (с точностью до выбора порядка ходов, что в данном случае несущественно). [c.666]
Дерево игры показано на Рис. 168. R обозначает забрать деньги , L — не забирать . Игра происходит в 2 этапа, на каждом из которых вкладчики одновременно решают, забирать ли деньги. Первый этап происходит по прошествии 1 месяца после вложения денег, второй — по прошествии 2 месяцев. [c.668]
| Рисунок 168. Дерево игры Набеги на банки | 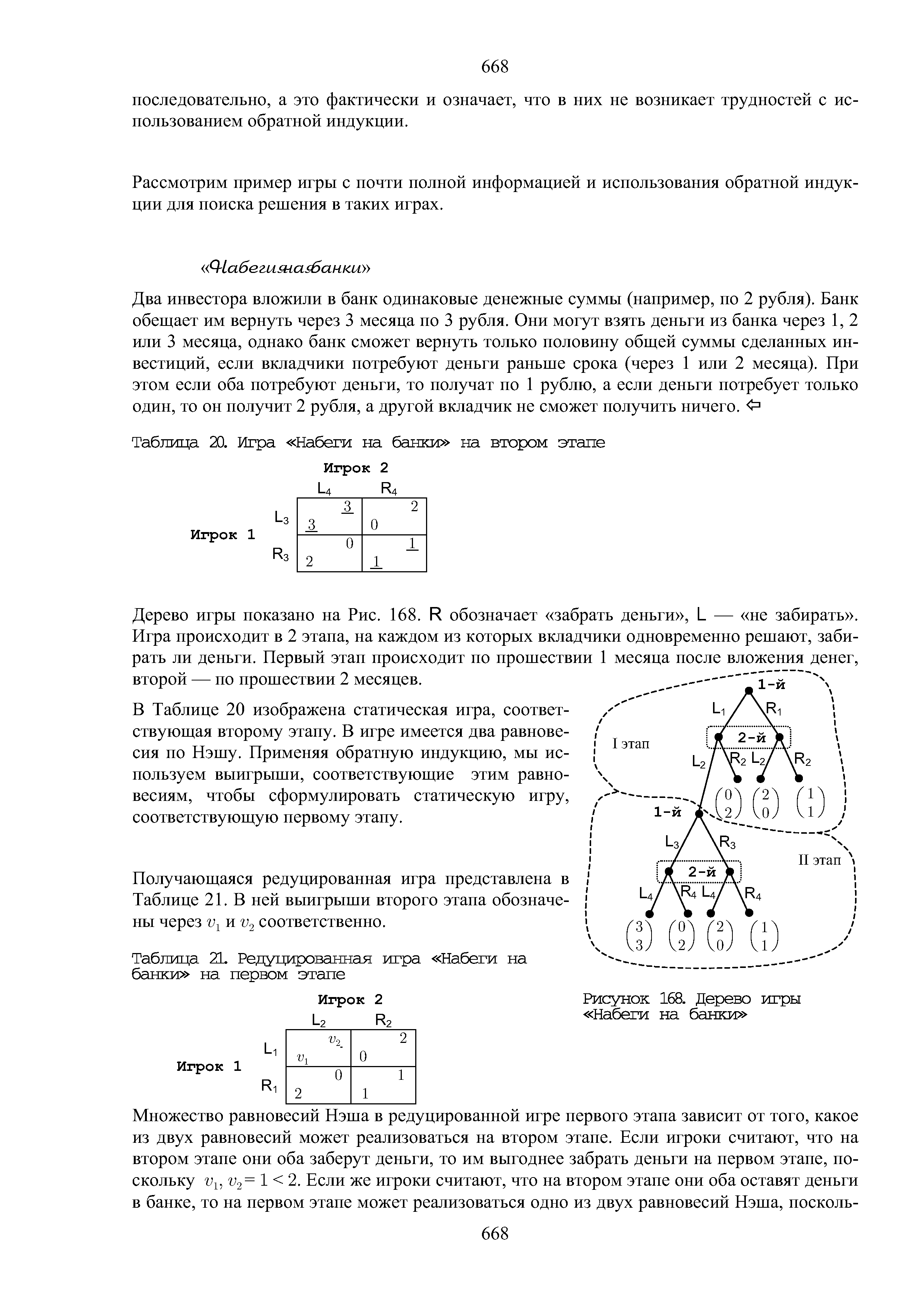 |
Аналогично, чтобы получить дерево п раз повторяющейся игры, следует к каждой конечной вершине та-1 раз повторяющейся игры прикрепить дерево исходной игры. Конечно, для описания повторяющейся игры не обязательно задавать все дерево игры, достаточно указать исходную игру и сколько раз она повторяется. В отличие от обычных игр, в повторяющихся играх принято сопоставлять выигрыши не только конечным вершинам, но и тем промежуточным, которые соответствуют конечным вершинам исходной игры. Общий выигрыш рассчитывается суммированием выигрышей в вершинах, лежащих на траектории игры. Таким образом, если utj — выигрыш, полученный г-м игроком в результате j-то повторения игры (на j-м раунде ), то общий выигрыш в п раз повторяющейся игре составит [c.689]
Рассмотрим эту игру при п = 3. На Рис. 179 показано дерево игры. [c.692]
Позиционная форма представляется деревом игры, которое можно рассматривать как обобщение дерева принятия решений, используемое в теории принятия решений, на случай нескольких игроков. Формальное определение мы приведем в гл. 2. "Древесная структура" описывает, какая вершина следует за какой, какой игрок имеет ход, в соответствующей вершине. Информация, которую имеют игроки, описывается с помощью информационных множеств. (См. рис. 1). Если две вершины лежат в одном информационном множестве, то это означает, что игрок (в данном случае 3) не может сказать, какое из двух действий (Л или П) в действительности произошло (в этом смысле игрок не различает вершины дерева, лежащие в одном информационном множестве). [c.24]
В игре с совершенной информацией каждый игрок всегда знает точно, в каком месте дерева игры он находится, нет одновременных ходов, и все игроки наблюдают ходы Природы (если таковые есть). [c.83]
Формально позиционная форма игры описывается с помощью следующих элементов списка игроков дерева игры указания для каждой вершины номера игрока [c.84]
Мы имеем дерево игры с конечным множеством вершин X и конечным множеством ходов А. [c.85]
Начинаем с конца дерева игры, и определяем равновесия по Нэшу для каждой из "концевых" под-игр, т.е. под-игр, не имеющих собственных под-игр. [c.98]
В директивной экономике жестко структурируется вся экономическая система (по отраслевому признаку), при этом главенствующую роль играют министерства и ведомства. Любую отрасль схематично можно представить в виде перевернутого дерева корень, т. е. основа дерева — это министерство, крона — подведомственные управления, объединения, организации, предприятия, ветвящиеся , т. е. упорядоченные в виде некой иерархической структуры. Министерство определяет плановые задания по наиболее важным показателям, которые в дальнейшем спускаются по подведомственным элементам данной структуры. В свою очередь, сведения о выполнении установленных плановых заданий проходят в точности обратный путь и, постепенно агрегируясь, попадают на высший уровень — в министерство. [c.331]
Есть моменты, когда происходит что-то совершенно неожиданное, например, землетрясения. Однако, несмотря на степень неожиданности, кажется, можно заключить, что любое подобное событие очень быстро сбрасывается со счетов без разворота существующего до этого события направления движения. Те, кто считает новость причиной движения рынка, возможно, будут более удачливы в игре на ипподромах, чем полагаясь на свои способности правильно угадать значение выдающейся новости. Следовательно, единственный способ "отчетливо увидеть лес" заключается в том, чтобы занять позицию над окружающими деревьями. [c.118]
ДЕРЕВО ИГРЫ [game tree] — способ описания игры с помощью графа "дерево", последовательно по ходам фиксирующего, какой информацией располагают игроки перед каждым ходом, какие варианты они могут выбирать и какими могут быть предельные размеры платежей в конце игры. Игра, описываемая с помощью подобного "дерева", называется игрой в развернутой (экстенсивной) форме, а иногда — позиционной игрой. [c.77]
Вершины дерева игры называются позициями позиции, непосредственно следующие за некоторой позицией, называются альтернативами позиции, не имеющие альтернатив, называются окончательными, а ведущие в них пути - партиями (так, описанная игра имеет четыре партии). Часть дерева решений, описывающая игру из некоторой позиции после нескольких начальных шагов партнеров, называется подыграй, и ее решение может представлять самостоятельную задачу. (Хорошим примером подыгр являются шахматные этюды типа "За сколько шагов из данной позиции белые смогут поставить мат черному королю ") [c.241]
| Рисунок 93. Дерево игры для модели Акерлова при полной информированности |  |
Кофе — рынок, зависящий от погоды. Зима в Латинской Америке совпадает е детом в Северном полушарии. В истории известны случаи, когда пжи-даиие заморозков, угрожа я тих деревьям в июне и июле, подбрасывало фьючерсные цены резко вверх. Засуха гак же играет свою роль. R период, начинающийся с 1975 г., фьючерсные цены колебались от 4.5 центон la фунт до 53,40 за фут, что представляет собой движение в 755 процентов. [c.190]
