I квадрант матрицы разбивается на четыре подматрицы. Матрица А представляет собой нормативную матрицу прямых затрат, отражающих непосредственно расход одного продукта на производство другого. [c.228]
Для машиностроительных предприятий, где продукция получается в результате определенной комбинации ее составных частей (узлов, приборов, деталей), связи. между Аг, А2 и А 3 слабы, имеет смысл говорить об обратных связях только для вспомогательных производств. Рассмотрим подматрицу прямых нормативных затрат между вспомогательными цехами Свердловского машиностроительного завода им. Воровского (табл. 10.1). Коэффициенты этой подматрицы представляют собой стабильные величины, так как технологический процесс на машиностроительном предприятии носит устойчивый характер. Вычислив ап- = - -,.со- [c.229]
| Таблица 10.1 Подматрица Прямых нормативных затрат между вспомогательными цехами | 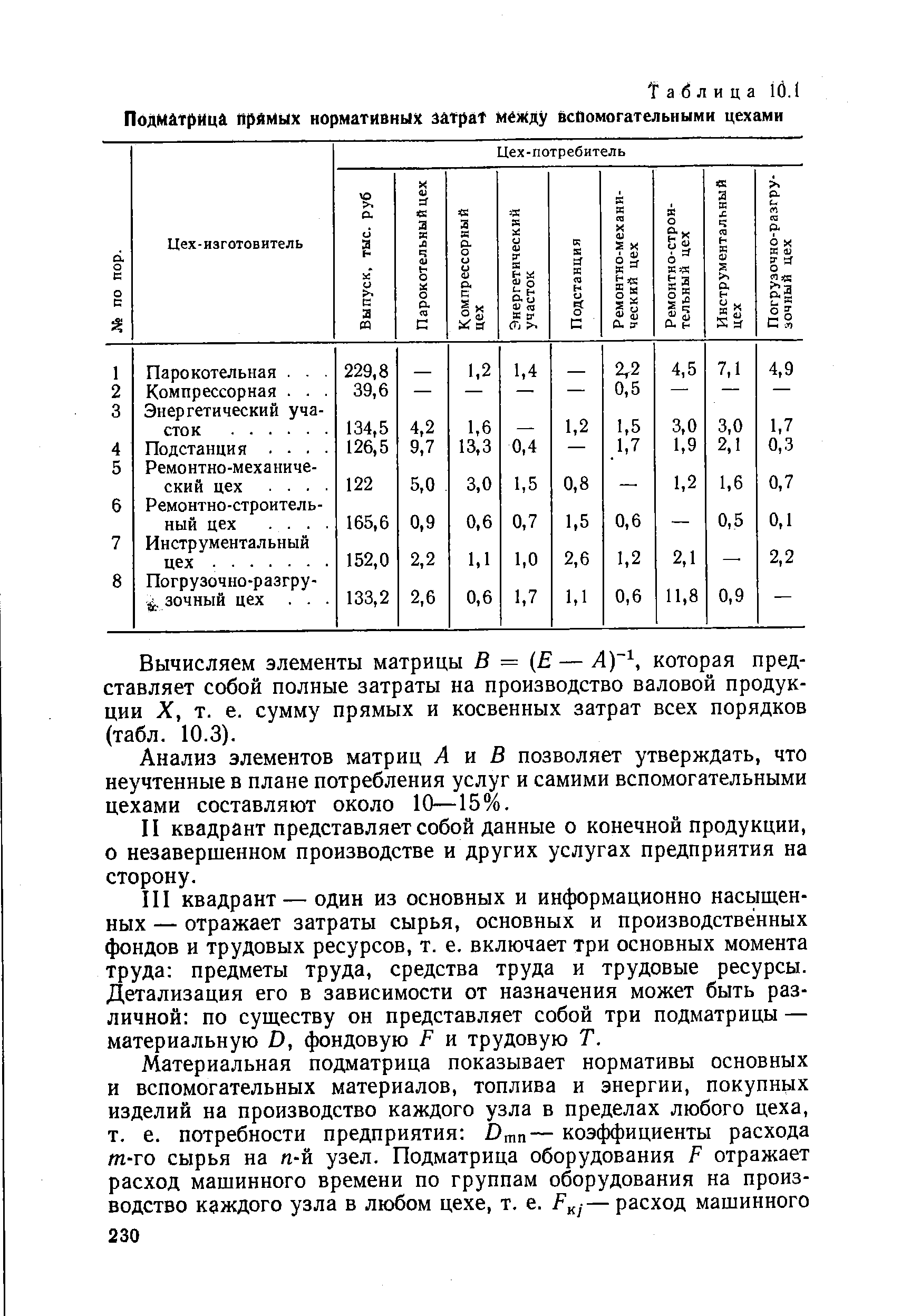 |
III квадрант — один из основных и информационно насыщенных — отражает затраты сырья, основных и производственных фондов и трудовых ресурсов, т. е. включает три основных момента труда предметы труда, средства труда и трудовые ресурсы. Детализация его в зависимости от назначения может быть различной по существу он представляет собой три подматрицы — материальную D, фондовую F и трудовую Т. [c.230]
Материальная подматрица показывает нормативы основных и вспомогательных материалов, топлива и энергии, покупных изделий на производство каждого узла в пределах любого цеха, т. е. потребности предприятия Ьтп— коэффициенты расхода m-го сырья на n-й узел. Подматрица оборудования F отражает расход машинного времени по группам оборудования на производство каждого узла в любом цехе, т. е. FKj—расход машинного [c.230]
Разобьем матрицы А, X и С на подматрицы (клетки) в соответствии с принятым базисным решением - исходным (или опорным) планом. [c.74]
Матрица А разбивается на подматрицы А0 и As, причем А0 содержит столбцы, соответствующие коэффициентам при переменных х5 и х6, равных нулю, а матрица As представляет собой столбцы, соответствующие коэффициентам при остальных (базисных) переменных [c.74]
Матрица X разбивается на подматрицы Х0 и Х , причем XQ содержит значения переменных, равных нулю, a Xs - значения остальных (базисных) переменных [c.74]
Матрица С разбивается на подматрицы С0 и s, причем С0 содержит коэффициенты в выражении для линейной формы при нулевых переменных, a s - для остальных (базисных) переменных [c.74]
Ее ранг равен 3, так как определитель квадратной подматрицы 3x3 этой матрицы не равен нулю [c.119]
ML, транспонированная по отношению к А = [а.] есть М. того же размера, у которой столбцы поменялись местами со строками. Иначе говоря, это [я.1. Обратные и транспонированные М. имеют очень большое применение в моделях МОБ. В них также широко применяется разбиение М. на меньшие подматрицы (блоки). М. коэффициентов систем уравнений — инструмент решения задач математического программирования, задач линейной алгебры и др. [c.187]
Пусть В—(,) = (АК АЦ- ---,АЫ (Л — базисная подматрица, т.е. матрица, составленная из столбцов (N S),N S. .,N -S> [c.448]
Следовательно, (r,s) = 3, (r,s) = (3,4). Правая подматрица [c.529]
Следовательно, 0(r,s) = 3, (r,s) — (4,1). Правая подматрица [c.530]
Подматрица матрицы Л есть прямоугольный массив, полученный из Л вычеркиванием некоторых строк и столбцов. Минором называется определитель квадратной подматрицы Л. Минором элемента а - называется определитель подматрицы Л, полученной вычеркиванием ее г-й строки и j-ro столбца. Алгебраическим дополнением а -, обозначаемым с -, называется произведение (— 1)г+-7 на минор aij. Матрица С = ( ij) называется матрицей алгебраических дополнений матрицы А. Транспонированная к С матрица называется присоединенной к Л и обозначается А . Имеем [c.30]
Для произвольной квадратной матрицы А ее главная подматрица получается вычеркиванием одинаковых (по номеру) строк и столбцов. Определитель главной подматрицы называется главным минором. [c.30]
Пусть матрица В размера т х п аналогичным образом разбита на подматрицы Bij (г, j = 1, 2). Тогда [c.31]
Пусть теперь п х р матрица С разбита на подматрицы ij (г, j = 1,2) таким образом, что Си имеет HI строк (и, следовательно, С <2 также имеет п строк, [c.31]
Как уже упоминалось в 1.9, алгебраическое дополнение ij произвольного элемента a j квадратной матрицы Л определяется как произведение (—1) +J на определитель подматрицы, полученной из А вычеркиванием строки г и столбца j. Матрица С = (с -) называется матрицей алгебраических дополнений матрицы Л. Матрица, транспонированная по отношению к (7, называется матрицей, присоединенной к Л, что будет обозначаться как [c.69]
Пусть А — симметрическая матрица порядка п, а В — матрица размера т х п полного ранга по строкам га. Пусть Агг обозначает квадратную подматрицу порядка г в верхнем левом углу Л, а Вг — матрицу размера га х г, составленную из первых г столбцов В (г = 1,.. . , п). Будем считать, что Вт ф 0. Определим квадратные матрицы порядка га + г [c.85]
Уравнение (13) показывает, что последние п — т столбцов Е линейно выражаются через 7П первых. Значит, г(Е) га. Но так как Dig( ) — подматрица Е и ее ранг равен га, ранг самой Е не может быть меньше га. Таким образом, [c.181]
БЛОЧНАЯ МАТРИЦА [partitioned matrix] — матрица, разбитая вертикальными и горизонтальными линиями на "блоки", подматрицы, которые являются в свою очередь матрицами меньших размеров и при выполнении тех или иных действий над ней рассматриваются как ее элементы. [c.33]
Для наглядности математического описания систем электроснабжения целесообразно однородные электроприемники объединить в отдельные группы и представлять их в виде подматриц. Например, группа распределительных подстанций, группа силовых трансформаторов, группа асинхронных двигателей, группа синхронных двигателей и т.д. [c.34]
В матрице (1.13) и1, п2 и пЬ — количество присоединенных к каждой секции распределительных шин напряжением 6 кВ соответственно высоковольтных асинхронных двигателей, синхронных двигателей и прочей нагрузки в произвольно выбранной РТП. Если к каждой секции присоединено различное количество однородных электротехнических устройств и электроприемников, то соответствующие элементы матрицы оставляют пустыми. К секциям распределительных шин на третьем уровне системы электроснабжения присоединены четыре группы однородных электроприемников, поэтому матрица (1.13) разделена на четыре подматрицы. [c.34]
В матрице (1.14) я и 2 - количество присоединенных к каждой секции распределительных шин напряжением 0,4 кВ соответственно низковольтных асинхронных двигателей и прочей нагрузки. Данная матрица разделена на две подматрицы, так как на втором уровне системы электроснабжения имеются две группы однородных электроприемников. Если количество однородных электроприемников, присоединенных к каждой секции распределительных шин, неодинаковое, то соответствующие элементы матрицы также оставляют пустыми. [c.35]
Структура пакета представляет пользователю широкие возможности корректировки исходной матрицы, модификации задача и проведения по-слеолтимизацаояяого анализа. Кроме того созданы дополнительные программы для замены и удаления отдельных записей из исходного массива, записанного на языке ППП "Линейное программирование в АСУ1 1-, а гаквв программы формирования подматрицы А матрицы А для выполнения конкретного портфеля нарядов-заказов z - ( ylt пц ) <ет и преобразования решения, выдаваемого пакетом "Линейное программирование в АСУ s форме таблиц нескольких типов. [c.49]
Пусть AI — симметрическая матрица порядка п + 1. Мы хотим представить матрицы Dfn l(Ai 0 Ai)Dn+i и D l(Ai 0 i)D +1 в виде блочных матриц. В частности, нас будет интересовать, является ли матрица Dfn(A 0 A)Dn подматрицей D n+l(Ai 0 i)Dn+i, а (Л 0 A)D+ — подматрицей D +l(Ai [c.82]
