Что касается первого вопроса, то в качестве примера, по крайней мере, не вполне оправданного применения математики в экономике можно привести известный в анализе хозяйственной деятельности интегральный метод факторного анализа. Его разработчики, безжалостно критикуя простой и наглядный метод цепных подстановок, говорят о том, что интегральный метод "обеспечивает более высокую точность". Не вдаваясь в комментарий относительно точности в рамках ретроспективного анализа, отмечу только, что обоснованность применения интегрального метода в экономике является исключительно условной, поскольку он требует непрерывности функции, описывающей факторную связь, и бесконечно малого изменения признаков, чего в экономических явлениях часто не может быть в принципе, поскольку многие показатели изменяются дискретно. [c.315]
| Рис. 56. Усиление степенной зависимости размера s (в условных единицах) типичной самой большой группы как функция силы подражания К. По мере приближения /С к Кс, s отклоняется. Это отклонение воплощает наблюдение, что бесконечно большие группы формируются в критической точке Кс. На практике же, s ограничена размером системы. | 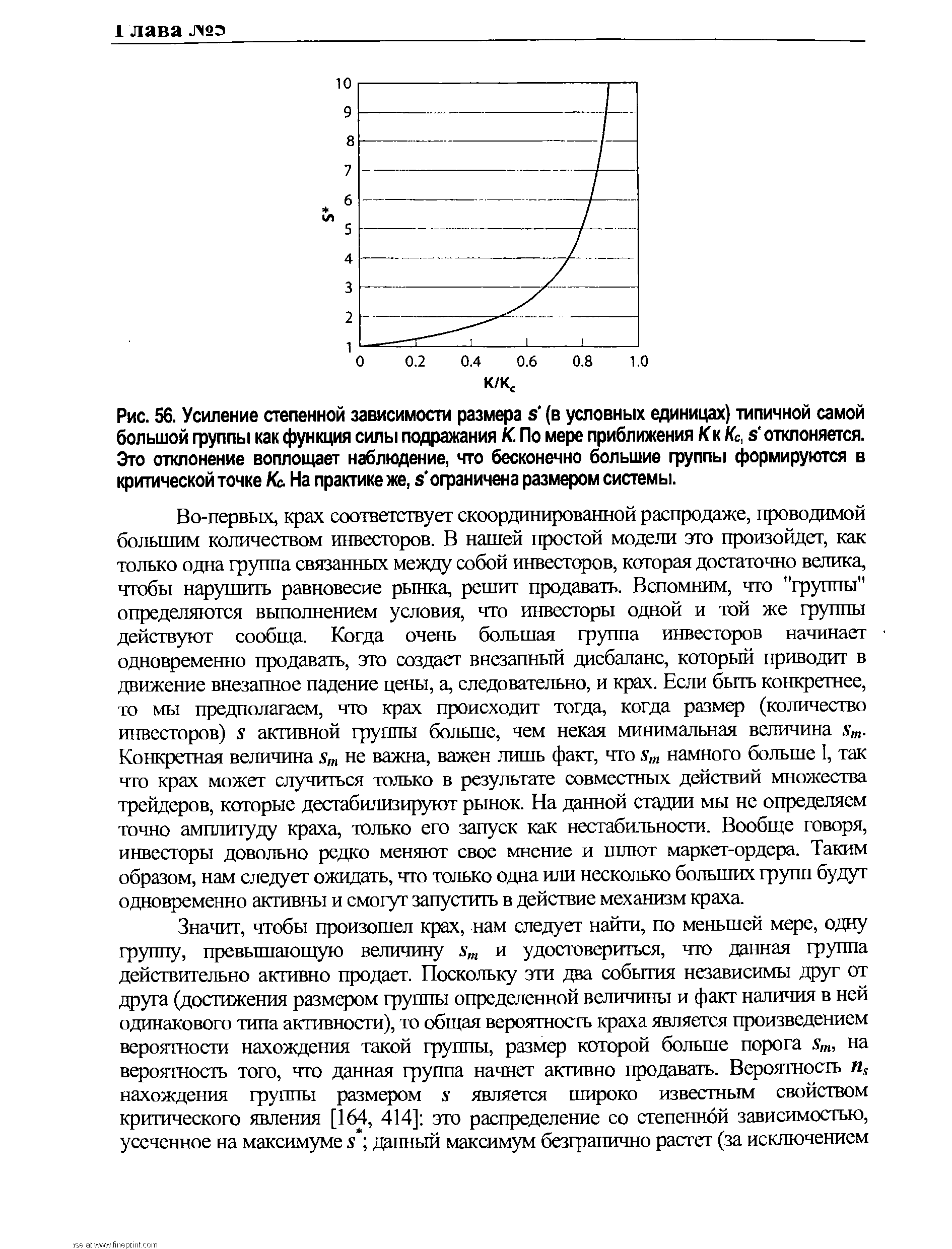 |
Вы можете начать с очень небольшого количества условных обозначений и увеличить его, когда в этом возникнет необходимость. Возможности бесконечны. Почти в каждой записи вашего календаря будет четко обозначено то или иное лицо ( кто ), которое повлияло на достигнутые результаты. [c.374]
При этом Р (Q) = 1 и если А и В не пересекаются, то Р (A (J В)—Р (A) +P (В). Отношение Рв = Р (А ( ] В)/Р (В), где Р (В) > 0, называется условной вероятностью события А при условии В. Если S содержит бесконечное число событий, то для каждой [c.19]
Второй случай — абсолютно эластичный спрос — характеризуется параллельной оси абсцисс Q кривой спроса Dr По данной цене можно реализовать сколько угодно продукции. Но если вырастет цена, то покупатели откажутся покупать ее. Однако экономическая наука таких примеров не знает, и это естественно, так как бесконечного возрастания спроса в экономике не бывает. Пример здесь. скорее — условный. [c.147]
Имея в виду эти результаты, я хотел бы предложить следующее для рынков акций и облигаций. В краткосрочной перспективе на рынках доминируют процессы торговли, которые являются дробными шумовыми процессами. В местном масштабе они являются членами семейства AR H-процессов и характеризуются условными дисперсиями то есть каждый инвестиционный горизонт характеризуется своим собственным измеримым процессом AR H с конечной, условной дисперсией. Эта конечная условная дисперсия может использоваться для оценки риска только для этого инвестиционного горизонта. В глобальном масштабе данный процесс является устойчивым (фрактальным) распределением Леви с бесконечной дисперсией. По мере увеличения инвестиционного горизонта он приближается к поведению бесконечной дисперсии. [c.257]
Приведенный пример в значительной мере является условным, польку вариантов значений доходности акций на реальном фондовом ке бесконечное число (в частности, отметим, что цена акции может из- яться, принимать новые значения). Следствием этого является то, что пбчатая диаграмма трансформируется в непрерывную кривую - кри-> плотности распределения вероятностей значений доходности (рис. 3.9). >тность вероятности значений доходности есть функция [c.67]
Приемов факторного анализа много, однако верхом аналитического совершенства считался так называемый интегральный метод, с помощью которого, по мнению его сторонников, можно было рассчитать факторные разложения с более высокой точностью1. Этот метод был заимствован из математики, причем без какого-либо осмысления возможности и оправданности его приложения к экономике. В математическом анализе соответствующий метод (разложение в ряд Тейлора) используется в условиях диф-ференцируемости функции, описывающей изучаемую взаимосвязь, и бесконечно малого изменения признаков, чего в экономике не может быть в принципе, так как многие показатели изменяются дискретно. Однако если даже абстрагироваться от этих формальных требований, то без какой-либо натяжки можно утверждать, что интегральный метод - лишь один из возможных способов факторного разложения, он не хуже и не лучше других, поскольку любое подобное разложение исключительно условно по самой своей сути. Если же подойти к этому вопросу критически, то несложно показать, что все подобные методы (дифференциальный, интегральный, логарифмический и др.) скорее вредны, нежели полезны, поскольку за счет утяжеления (именно утяжеления, а не усложнения) счетных процедур создается видимость серьезности анализа. Любые разговоры о преимуществе одних методов факторного анализа над другими, выражающемся в большей точности разложения (а это основной аргумент апологетов интегрального метода), представляют собой не более чем голословные утверждения. Кроме того, даже на мгновение согласившись с этим абсурдным утверждением, все же нельзя получить более или менее вразумительный ответ на вполне резонный вопрос а зачем нужна эта точность в приложении к ретроспективному анализу Поезд-то уже ушел Если же попытаться применить интегральный метод в перспективном анализе, то и здесь он абсолютно бессмыслен, поскольку исходный материал в этом случае - исключительно приблизительные прогнозные значения показателей. Иными словами, в любом случае анализ с помощью интегрального метода - это также игра в цифирьки , а пресловутая точность метода - не более чем лозунговый блеф. Применять интегральный метод - все равно что строгать скальпелем кол для изгороди строгать-то можно, только вот зачем [c.348]
