| Рис. 15.2. Фронты эффективных портфелей из 3, 4 и 5 активов | 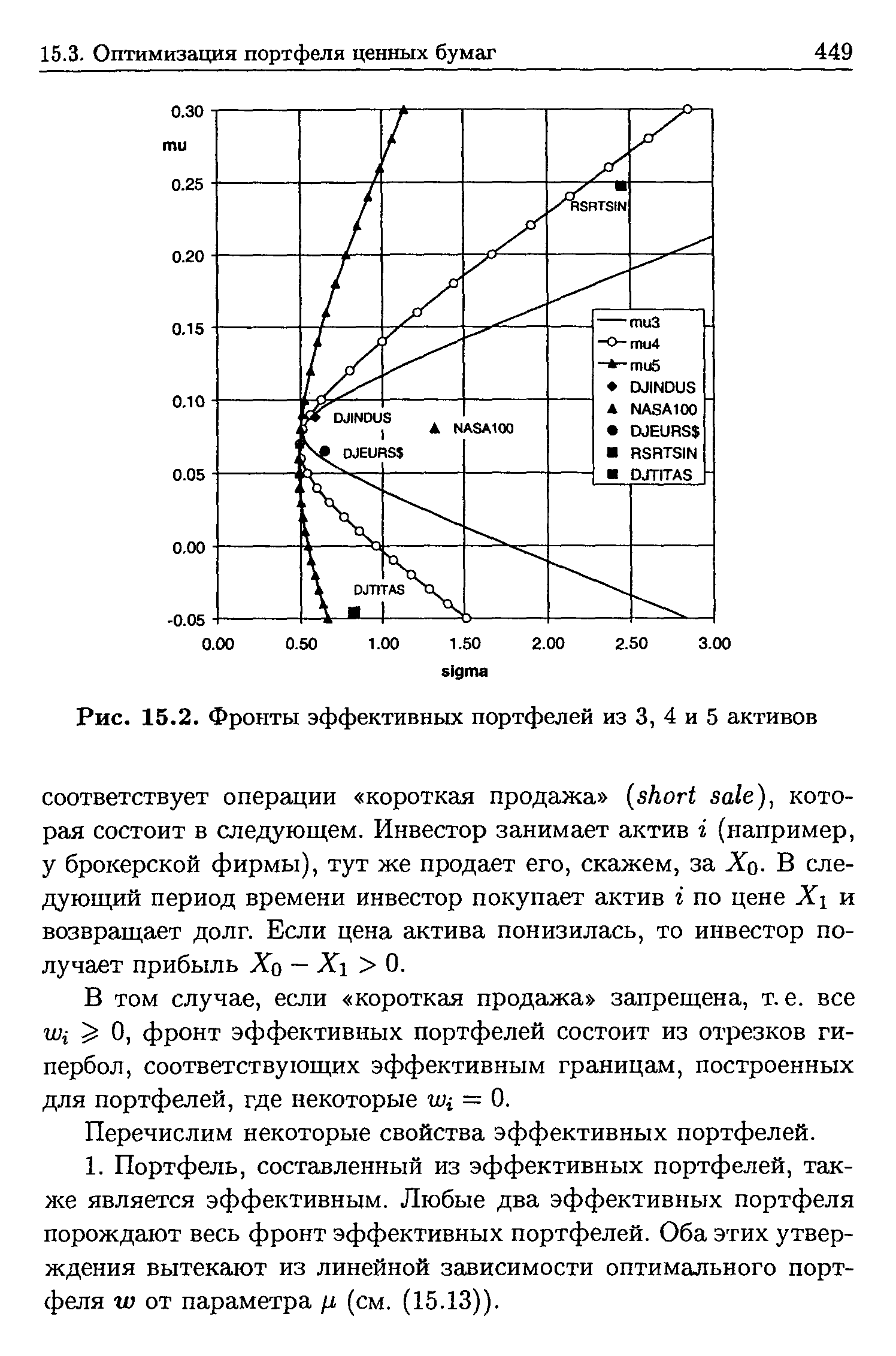 |
Портфель, составленный из эффективных портфелей, также является эффективным. Любые два эффективных портфеля порождают весь фронт эффективных портфелей. Оба этих утверждения вытекают из линейной зависимости оптимального портфеля w от параметра /J, (см. (15.13)). [c.449]
Из рис. 15.2 мы видим, что с включением в портфель новых активов фронт эффективных портфелей сдвигается влево. Это означает, что инвестор может сформировать эффективный портфель с той же средней доходностью /х, но с меньшей дисперсией (риском). Остается, однако, вопрос является ли этот сдвиг статистически значимым Имеет ли смысл инвестору включать дополнительные активы в свой портфель В этом разделе мы приведем тест, помогающий ответить на этот вопрос. [c.450]
Пусть есть инвестор, который уже инвестировал в множество X из п активов. Обозначим вектор их доходностей через гх — (-Rx.i) Rx,n Множеству X соответствует фронт эффективных портфелей. Зададимся вопросом сдвигается ли этот фронт, если добавляется возможность дополнительного инвестирования в набор У из m активов Ниже мы используем следующие обозначения все величины, имеющие отношение к портфелю, [c.450]
Поскольку мы предположили, что фронты эффективных портфелей совпадают для портфелей, составленных из активов X и У и составленных только из активов X, то равенство (15.21) должно выполняться для всех ц. Отсюда вытекает, что коэффициенты при 7/i и в в обеих частях равенства совпадают. Получаем систему уравнений [c.451]
Рассмотрим вопрос о необходимости включения нового актива в портфель с другой точки зрения. Теперь нас будет интересовать статистическая значимость сдвига фронта эффективных портфелей при включении нового актива только в точке, соответствующей оптимальному портфелю с заданной ожидаемой доходностью (j,. Значимо ли уменьшится риск при включении нового актива в портфель [c.454]
Один из способов найти фронт эффективных портфелей в случае присутствия безрискового актива аналогичен предыдущему (15.8)-(15.12) мы предоставляем читателю проделать его самостоятельно (см. упражнение 15.3). [c.456]
Здесь мы приведем геометрически более наглядный вывод. На рис. 15.3 представлен фронт эффективных портфелей для тех же четырех активов, что и на рис. 15.2. Справа от гиперболы находится множество достижимых портфелей, т. е. таких точек плоскости ( r,/J-), которые соответствуют хотя бы одному портфелю. Пусть wp — портфель активов с ожидаемой доходностью цр и дисперсией доходности а . [c.456]
| Рис. 15.3. Фронт эффективных портфелей при наличии безрискового | 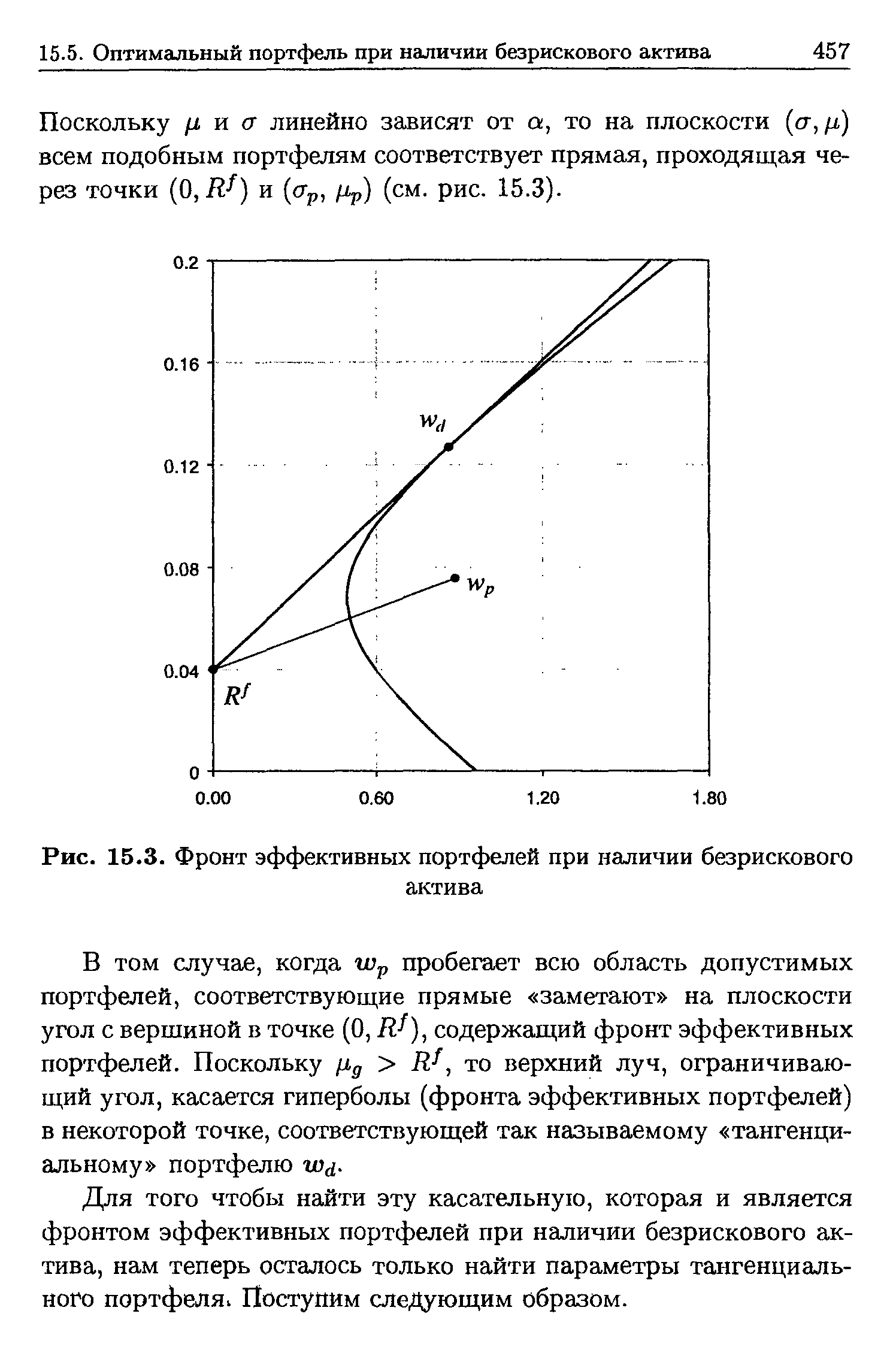 |
Для того чтобы найти эту касательную, которая и является фронтом эффективных портфелей при наличии безрискового актива, нам теперь осталось только найти параметры тангенциального портфеля Поступим следующим образом. [c.457]
На рис. 15.3 представлен луч, соответствующий фронту эффективных портфелей, включающих безрисковый актив с доходностью Rf = 0.04. [c.459]
Очевидно, что положение касательной не изменится тогда и только тогда, когда при включении дополнительного актива не изменится тангенциальный портфель, что означает, что старый и новый фронты эффективных портфелей без безрискового актива (гиперболы) касаются друг друга в точке, соответствующей тангенциальному портфелю w . [c.459]
Проведем касательную к фронту эффективных портфелей (гиперболе) в некоторой точке (<гр, /хр), принадлежащей фронту и, следовательно, удовлетворяющей уравнению (15.15). Уравнение касательной имеет вид [c.459]
Прежде чем перейти к моделям оценки финансовых активов, покажем, как с помощью приведенного выше формализма получается вывод теории фронта эффективных портфелей. [c.463]
Фронт эффективных портфелей [c.463]
Мы видим, что 7 определяет однозначно ожидаемую доходность портфеля, а дисперсия доходности минимальна при п = 0. Таким образом, все эффективные портфели описываются равенством R = R + jRe, и фронт эффективных портфелей (гипербола на плоскости (ст, (J,)) задается парой уравнений [c.465]
Разным значениям ожидаемой доходности /х соответствуют разные оптимальные портфели го(/л) и, соответственно, разные значения дисперсий портфелей. Поскольку из (15.13) следует, что го( ) является линейной функцией /z, то из (15.7) видно, что дисперсия (риск) портфеля является квадратичным многочленом от /LI, принимающим только положительные значения и, значит, имеющим положительный коэффициент при /z2. Поэтому на плоскости (а, ц) точки, соответствующие различным значениям /LI, лежат на гиперболе. Эта гипербола состоит из оптимальных (эффективных) портфелей и называется фронт эффективных портфелей или граница эффективных портфелей (effi ient frontier). [c.448]
Справа от фронта эффективных портфелей лежит множество достижимых портфелей (feasible set). Заметим, что из (15.13) не следует, что все Wi неотрицательны. Отрицательное значение Wi [c.448]
