В рассмотренном выше примере (дискретные процессы снабжения и отпуска) продолжительность интервала поставки была больше величины одного интервала отпуска. Выражение, приведенное в формуле (5.31), отражает связь между нормообразующими факторами, определяющими расход производственного запаса в интервале поставки при данных условиях. Выражение в квадратных скобках в этой формуле учитывает, сколько на самом деле отпусков в производство рассматриваемой марки было в интервале между поставками. Очевидно, что по количеству дней оно было меньше продолжительности самого интервала поставки. Дело в том, что выражение (S — 1) отражает продолжительность одного перерыва между отпусками, а единица — это значение дня, в который непосредственно производился отпуск материала. Отняв от продолжительности интервала между отпусками (5) один день, получаем продолжительность самого перерыва между отпусками. Произведение (S — 1) х N отражает суммарный промежуток времени (в сутках) в интервале между поставками, в котором отпуски материала не осуществлялись. Разница между продолжительностью интервала между поставками и продолжительностью суммарного перерыва (выражение в квадратных скобках) определяет промежуток времени, т.е. общее количество дней, в который производились отпуски материала. [c.236]
На графике, приведенном на рис. 5.10д, показано изменение запаса при дискретных процессах снабжения и отпуска, когда продолжительность интервала поставки меньше значения интервала отпуска. При данных условиях происходит постепенное накопление запаса в течение интервала отпуска в результате осуществления поставок топлива. Затем в конце этого периода запас расходуется. Такие случаи формирования запасов возможны, например, в морском или рыбном порту, когда нужно заправить перед отходом в дальнее плавание танкер или судно с большим водоизмещением [c.236]
На графике, приведенном на рис. 5.106, показано изменение производственного запаса в интервалах, когда процесс снабжения нормируемой марки материала у потребителя будет дискретным, а процесс ее отпуска — непрерывным, причем оба процесса неравномерны, но согласованы между собой. У потребителя в этом случае поставки материала осуществляются разными объемами и через разные по продолжительности промежутки времени (разные интервалы поставки). В интервалах по дням меняются объемы суточных отпусков материала. Но при этом в каждом интервале объем поставки точно соответствует суммарному объему отпуска за соответствующий интервал, т.е. процессы снабжения и отпуска согласованы между собой. Эти процессы в данном случае коррелируют между собой, и коэффициент корреляции, определяющий степень связи между ними, равен единице. Аналогичная картина может иметь место и при дискретных процессах снабжения и отпуска. [c.240]
Необходимо отметить, что точки зрения указанных выше авторов на рассматриваемый вопрос довольно различны. В связи с этим авторами настоящего учебного пособия был специально проведен анализ изменения запасов в интервалах для разных условий их (запасов) формирования. Это позволило определить имеющее место соотношение между средним и максимальным значениями запасов в интервале при равномерных и дискретных процессах снабжения и отпуска для разных случаев. Для этого были проведены последовательные расчеты для каких-то отдельных соотношений между интервалом поставки и интервалом отпуска. Полученные результаты были обобщены и по ним подобраны соответствующие аналитические зависимости. [c.255]
Перейдем к рассмотрению второго и третьего случаев формирования производственных запасов при равномерных и дискретных процессах снабжения и отпуска, когда значение интервала поставки не кратно величине интервала между отпусками. Особенность формирования запаса при данных условиях заключается в том, что процесс имеет циклический характер, т.е. характер изменения запасов повторяется по определенному циклу и различен в разных интервалах поставки одного цикла. Продол- [c.261]
В табл. 5.8 приведен полученный выше результат вместе с другими обобщающими расчетами для разных случаев формирования запасов (для других соотношений между интервалами поставки и отпуска) при дискретных процессах снабжения и отпуска, когда значение интервала поставки больше величины интервала отпуска (Г > 5) и при этом значение первого (интервала поставки) не кратно второму, но эти значения имеют общий делитель. [c.266]
Примерно аналогичные подходы были применены в расчете при равномерных и дискретных процессах снабжения и отпуска для случаев, когда значение интервала поставки было меньше величины интервала отпуска. В этом случае использованы те же соображения кратно или не кратно значение интервала отпуска величине интервала поставки, имеют или не имеют они общий делитель и т.д. В остальном методы построения графи- [c.269]
Вывод формул для равномерных и дискретных процессов снабжения (поступления) и расхода (т.е. отпуска), аналогичных (6.76) и (6.77), приведен в разд. 5.7 (формулы (5.47), (5.51), (5.54)). Они позволяют перейти от вычисленного максимального значения запаса к среднему, которое необходимо для установления нормы производственного запаса. При неравномерных и дискретных процессах снабжения и расхода имеет место небольшая доля однодневных интервалов между поставками (или между днями отпуска). Для них характерно другое соотношение между средним и максимальным значениями запасов по сравнению с равномерными и дискретными процессами поступления и отпуска. И оно должно быть учтено при расчете. Формула (6.77), в которую введена поправка а, позволяет это сделать, т.е. вычислить данное соотношение (между средним и максимальным значениями запаса) для неравномерных и дискретных процессов снабжения и расхода. Поправка а учитывает долю однодневных интервалов, которые могут иметь место при неравномерных процессах поступления и отпуска. Подставленные в формулу (6.77) значения r, %, v, в которых путем введения поправки исключено влияние однодневных интервалов, позволит свести определение коэффициента А, аналогичного по своей физической сути коэффициенту для равномерных и дискретных процессов снабжения и отпуска, к уже известным и ранее выведенным формулам (5.47), (5.51), (5.55), приведенным в разд. 5.7. [c.352]
При неравномерных и дискретных процессах снабжения и отпуска, а также при условии Т < S определение специфицированной нормы производственного запаса производится аналогично ранее рассмотренному методу при Т > S. Отличие здесь заключается в том, что, во-первых, учитываются изменения запасов в интервалах отпуска вместо интервалов [c.352]
Малая частота поставок, расход материала на предприятии в отдельные месяцы года, дискретные процессы снабжения и отпуска [c.358]
Дискретные процессы снабжения и отпуска [c.376]
Напишите формулы определения изменений текущих и страховых запасов в интервалах поставки для случая его формирования при дискретных процессах снабжения и отпуска. Объясните смысл показателей, входящих в эти формулы. [c.409]
Напишите формулы определения изменений текущих и страховых запасов в интервалах поставки для случая его формирования при дискретных процессах снабжения и отпуска и наличии корреляционной связи между нормообразующими факторами. Объясните смысл показателей, входящих в эти формулы. [c.409]
На рис. 1.2 показаны изменения запасов при дискретном процессе снабжения и непрерывном расходе для двух случаев 1) для равномерных процессов (рис. 1.2а), а второй — для неравномерных процессов (1.26). Под равномерным процессом снабжения (расхода) подразумеваются поставки (объемы суточных отпусков), произведенные одинаковыми объемами и через равные по продолжительности интервалы времени. [c.47]
| Рис. 1.2. Формирование производственного запаса марки материального ресурса при дискретном процессе снабжения и непрерывном процессе отпуска | 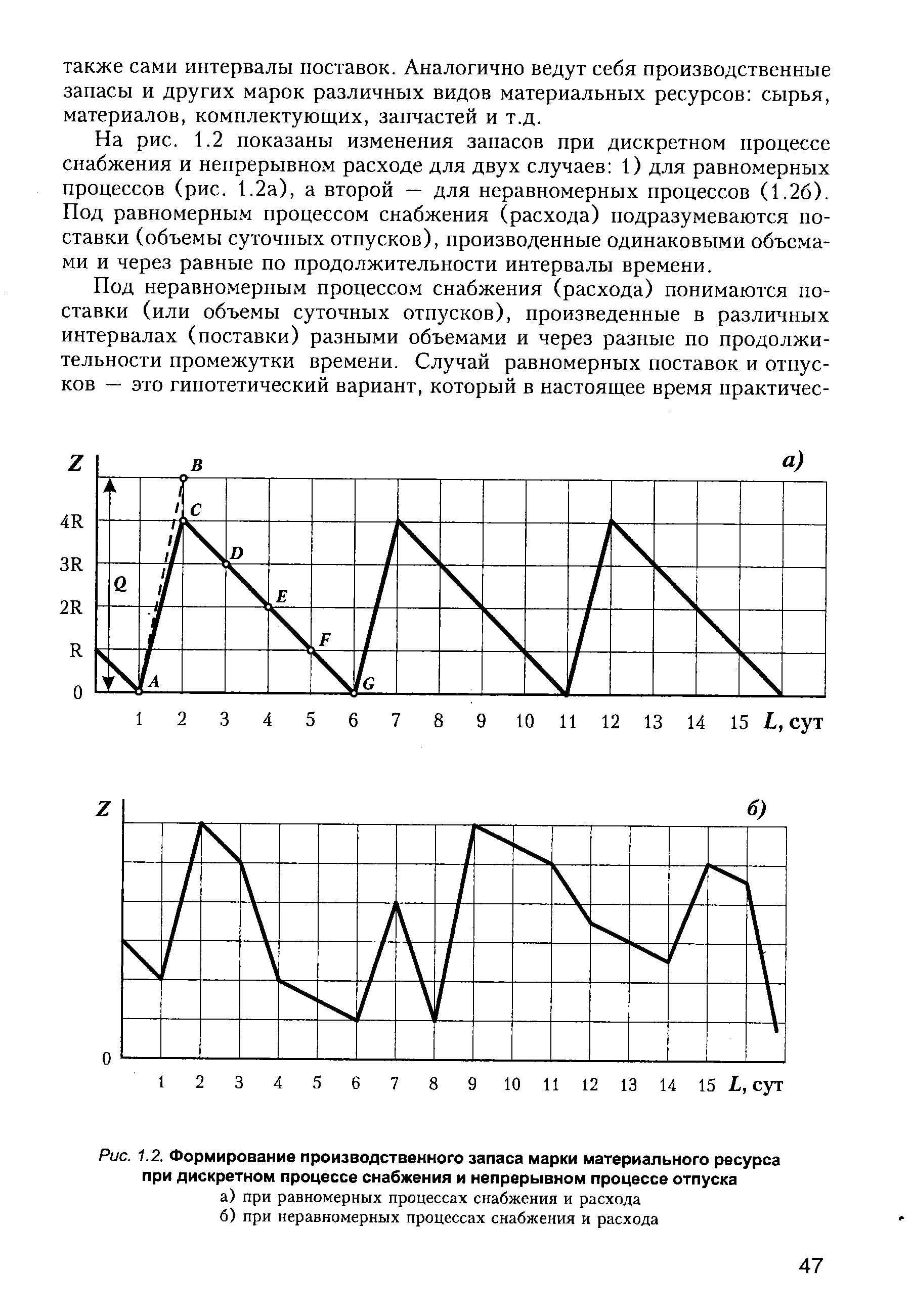 |
При дискретном процессе снабжения и непрерывном процессе расхода (см. рис. 5.10а) поставки осуществляются только в отдельные дни года, а отпуски — каждый день, при этом на графике показано изменение уровня запасов, когда оба эти процесса равномерные. Увеличение (накопление) запаса в начале каждого интервала, изображенное на графике, обусловлено поступлением марки материала на склад предприятия-потребителя, т.е. в результате выполнения операции процесса снабжения, а уменьшение запаса по дням в течение каждого интервала вызвано осуществлением отпусков материала со склада на производственные или хозяйственные нужды. Например, сырье, прокат, комплектующие и т.п. отпускаются в цехи предприятия на производственные нужды — для изготовления полученного заказа бензин отпускается для заправки автомобилей (на эксплуатационные расходы) запчасти выдаются цехам для проведения ремонта оборудования и транспортных средств мебель, компьютеры, калькуляторы, бумага, бланки, ручки и т.д. выдаются в отделы (плановый, финансовый, снабжения, сбыта, бухгалтерию) на хозяйственные нужды — для обеспечения выполнения служащими предприятия соответствующих функций. В данном случае рассматриваем изменение уровней запаса (суточных остатков) марки материала на складе и видим, что оно зависит от условий снабжения и расхода, т.е. сколько поступило или отпустили по суткам на предприятии. Из этого графика видно, что оба рассматриваемых процесса (поступление и отпуск) равномерны по объемам и времени, т.е. поставки осуществляются одними и теми же объемами и через равные интервалы времени, каждые сутки осуществляются отпуски материала одинаковыми [c.231]
Если произвести замену и в формулу (5.31) подставить значение 5, равное одному дню, что будет соответствовать случаю, когда отпуски рассматриваемой марки материала на предприятии осуществляются каждый день (непрерывный процесс ее расхода), а процесс снабжения этим материалом остается дискретным, то выражение в круглых скобках станет равным нулю. В этом случае произведение в квадратных скобках следует опустить, и эта формула соответственно превратится в формулу (5.29). При последующей замене, если в последнюю формулу подставить значение интервала поставки (Г), равное одному дню (в этом случае Т просто нужно заменить единицей), что соответствует случаю непрерывных процессов снабжения и отпуска, получим математическую связь по изменению запаса в интервалах для этих условий. Изменение уровня запасов (накопление и расход) в интервале поставки при данных условиях зависит уже только от двух нормообразующих факторов — объема поставки и объема суточного отпуска [c.239]
В реальных условиях вне зависимости от дискретности и непрерывности протекающих процессов снабжения и отпуска вообще возможны три следующих случая формирования запаса [c.240]
На графиках, приведенных на рис. 1.1, в качестве иллюстрации показаны изменения условий формирования запаса при неравномерных процессах снабжения и отпуска. Вообще характер их изменений в практике многообразен, и в общем случае они не похожи друг на друга. Из графиков видно, что меняются в течение года (а также в интервалах) все факторы интервалы и объемы поставок и отпусков. В отдельных интервалах, например, снабжение (процесс поступления марки материала у предприятия-потребителя) может быть как дискретным, так и непрерывным, аналогично процесс отпуска. Изменяются объемы и интервалы поставок и отпусков по величине, они могут чередоваться в совершенно произвольном порядке. Все это необходимо учесть при расчете специфицированной нормы производственного запаса. [c.241]
У ряда специалистов существует несколько противоречивых точек зрения на то, как соотносятся между собой среднее и максимальное значения запасов в интервале. Так, в работе [5, с. 12], как указывалось в гл. 3, средний запас рекомендуется определять, исходя из предположения, что поступивший материал отпускается после поставки через промежуток времени, равный интервалу отпуска. В связи с этим А. С. Айзенберг- Горский предлагает вычислять средний запас через сумму двух интервалов — поставки и отпуска (см. табл. 3.1). Противоположную точку зрения по этому вопросу высказывает А. И. Баскин в [5, с. 18]. Он считает, что средний запас необходимо находить через разность продолжительностей двух интервалов — из интервала поставки вычесть интервал отпуска. Н.Д. Фасоляк в [92, с. 91] предлагает вообще не учитывать продолжительность интервала отпуска при нормировании запаса. В последней из рассмотренных работ автор считает, что при дискретных процессах снабжения и расхода МР (или отпуска со склада, что то же самое по физическому смыслу) средний запас в году должен быть равен в днях расхода половине интервала поставки или в натурально-вещественном выражении — половине максимального запаса, что исключает необходимость учета интервала отпуска при расчете нормы. [c.254]
Очевидно, что при дискретных процессах поступления и расхода соотношение между максимальным и средним запасами не равно указанному выше значению — двум. Понятно, как можно рассчитать величину максимального запаса марки материала в начале интервала для дискретных процессов поступления и расхода. Вся сложность решения проблемы заключается в процессе перехода от максимальной величины к среднему значению. В целях анализа этой модели и разработки методологических подходов к расчету среднего значения рассмотрим условия формирования производственного запаса марки материала при дискретных процессах ее поступления и расхода у предприятия-потребителя при разных условиях формирования, т.е. при разных соотношениях между средним интервалом поставки и средним интервалом между отпусками. Проанализируем сначала случаи, когда процессы снабжения и отпуска равномерные. Этот случай представляет собой идеализированную модель формирования производственного запаса, рассмотрение которой помогает пояснить механизм его формирования в интервале поставки и обосновать подход к определению среднего значения запаса. [c.255]
Расчет соотношения между средним и максимальным значениями запасов в интервале при равномерных и дискретных процессах снабжения и расхода для случаев, когда интервал поставки больше интервала отпуска и значение интервала поставки кратно [c.262]
На рис. 5. 1 1г построен график изменения производственного запаса при дискретных и равномерных процессах снабжения и отпуска для случая, когда интервал поставки равен пяти суткам (7 = 5), а интервал между отпусками — двум суткам (5 = 2). Очевидно, что в этом случае интервал поставки не кратен интервалу между отпусками. На рисунке показано, что цикл начинается в начале года (1-го числа) и продолжается до окончания десятых суток (включительно), далее начинается новый цикл и т.д. Продолжительность цикла при данных условиях равна произведению значения интервала поставки и величины интервала отпуска (П = Т х 5). Физический смысл графика, приведенного на рис. 5. 11 г, заключается в следующем. В каждом из циклов укладываются два интервала поставки и пять интервалов отпуска. Поставки материала в рассматриваемом цикле были 1 и 6 января, а отпуски — 2-го, 4-го, б-го, 8-го и 10-го числа этого месяца. При этом 6-го числа в один день были произведены поставка и отпуск. Обе поставки были одинакового объема — q, все пять отпусков имели одну и ту же величину — г = (2/5) х q. На графике (рис. 5. Иг) показано, что первый интервал поставки продолжался с 1 но 5 января, второй — с 6-го по 10-е число, т.е. все они были пятидневные. Первый интервал отпуска начался 1 января и продолжался включительно по 2-е число, второй — с 3 по 4 января, следующий — с 5-го по 6-е число и т.д., все интервалы отпуска были одной продолжительности, которая равна двум суткам. Причем в каждом интервале (отпуска) первые сутки были днем перерыва, а вторые сутки — самим днем отпуска. [c.267]
Большая частота поставок, дискретный процесс снабжения и непрерывный процесс отпуска [c.304]
В случае когда у предприятия-потребителя процессы снабжения и отпуска неравномерны и дискретны, а материал у предприятия-поставщика изготавливается только в отдельные месяцы года, при расчете специфицированной нормы запаса следует руководствоваться указаниями, приведенными в разд. 6.4.3 и 6.4.6. [c.358]
Дискретный процесс снабжения и непрерывный процесс отпуска [c.361]
При дискретных процессах снабжения и расхода и соотношении значений продолжительностей средних интервалов, когда интервал поставки меньше интервала отпуска (Т < S ), необходимо учесть влияние вариаций значений четырех нормообразующих факторов второй группы интервалов поставок, объемов поставок, интервалов отпуска, количеств перерывов между поставками в интервалах отпуска. В этом случае для расчета специфицированной нормы производственного запаса, полученной на основе обработки исходной информации, использовать следующие данные [c.379]
В формуле (6.98), приведенной в разд. 6.5.3, xv — значение суммарного объема поставок в интервале отпуска в плановом периоде. При непрерывном процессе снабжения оно вычисляется как произведение продолжительности интервала отпуска и объема поставки. Здесь, при дискретном процессе снабжения (и при Гср < 5ср), оно вычисляется (формула (6.104)) как произведение числа дней поставок в интервале отпуска и его продолжительности (число дней поставок в интервале отпуска может быть меньше продолжительности самого интервала). [c.381]
Напишите формулу определения изменений страховых запасов в интервалах между поставками для случая их формирования при дискретном процессе снабжения и непрерывном процессе отпуска. Объясните смысл показателей, входящих в эту формулу. [c.409]
В качестве иллюстрации в табл. 1.6 показано, как у предприятий-потребителей разных отраслей экономики последовательно менялись в ограниченном временном отрезке года объемы поставок, в табл. 1.7 — интервалы поставок, в табл. 1.8 — объемы суточных отпусков. Данные в этих таблицах приведены в относительных величинах qt/Q , t,/T , rh/R , где q — фактический объем суточной поставки в 1-м. интервале (поставки , t[ — /-Й интервал поставки, rh — объем суточного отпуска. Здесь / — индекс (порядковый номер) интервала, h — индекс порядкового номера дня в году Q, Т, R — средние значения вариаций объемов поставок, интервалов поставок, объемов суточных отпусков соответственно1. Естественно, что количество поставок в году будет точно соответствовать числу интервалов поставок в данном периоде (поэтому для обозначения поставок и интервалов используется один и тот же индекс — /). Но при дискретном процессе снабжения и непрерывном процессе отпуска число поставок (или интервалов соответственно) обычно меньше количества суточных отпусков, поэтому они обозначаются разными индексами — Ink (см. табл. 1.6 и 1.8). [c.68]
На рис. 5.10а изображено, что в интервале поставки, который продолжался три дня, 2-го числа была произведена поставка рассматриваемой марки материала объемом Q т. В связи с этим уровень производственного запаса материала увеличился на предприятии на эту величину в данный день. Пунктиром показано, какой запас образовался после поставки, а сплошной линией на графике показан остаток материала на конец суток 2 января. Часть этого поступления пошла на восполнение подготовительного запаса, который был израсходован в день поставки в результате осуществления отпусков в эти сутки на производственные и хозяйственные нужды, а остальная часть — на увеличение уровня запаса на предприятии1. Если подготовительный запас принять равным одному дню, то в результате произведенной поставки уровень запаса на конец рассматриваемого дня (2 января) увеличился до значения Z = Q. Из него в дальнейшем (3, 4 января) покрываются все потребности предприятия в данном материале до следующей очередной поставки. В последующие дни, как это видно из графика (рис. 5.10а), уровень запаса каждый день постепенно снижается на постоянную величину, равную величине объема суточного отпуска — R. К концу интервала (4 января) накопленный запас будет полностью израсходован. А 5 января, в день очередной поставки, суточные потребности будут покрываться из подготовительного запаса. В последующих интервалах этот процесс многократно воспроизводится. Продолжительность каждого интервала (Г) при данных условиях будет равна трем суткам, а объем поставки (Q) соответствовать трем объемам суточных отпусков — Q = 3 х R. Естественно, что в других случаях при другой частоте поставок интервалы между ними (поставками) могут быть совершенно другой продолжительности 4, 5, 6 и т.д. суток, а объем поставки соответственно пропорционален этому количеству дней. Таким образом, при дискретном процессе снабжения и непрерывном процессе отпуска запас, образовавшийся (накопленный) в интервале, равен объему поставки, а израсходованный — произведению продолжительности интервала и объема суточных отпусков. Поскольку процесс отпуска непрерывный, то продолжительность интервала (в сутках) говорит о количестве дней, в которые производился отпуск. При этом образовавшиеся и израсходованные запасы в данное случае (при равномерных и согласованных процессах снабжения и отпуска) равны между собой. Изменение запаса (накопление и расход) в интервале поставки при этих условиях зависит от трех следующих нормообразующих факторов — объема поставки, объема суточного отпуска, интервала между поставками [c.232]
При расчете специфицированной нормы производственного запаса вероятностно-статистическим методом необходимо учесть условия формирования производственного запаса на предприятии. Особенность формирования при транзитных (складских, смешанных) поставках и указанных выше условиях (при дискретном процессе снабжения и непрерывном процессе отпуска) заключается в том, что любая из рассматриваемых марок МР поступает на предприятие не каждый день, но в больших количествах (например, в объеме железнодорожного вагона, железнодорожного маршрута и т.п.), а отпускается на производственные нужды ежедневно небольшими партиями, так, что произведенной поставки хватает для отпуска на несколько суток. При данных условиях следует учесть все нормообразующие факторы первой группы (см. разд. 1.2) и три нормообразующих фактора второй группы — вариации в течение года (квартала) объемов поставок, интервалов поставок и объемов суточных отпусков нормируемой марки материального ресурса1. [c.305]
В случае когда процессы снабжения и отпуска неравномерны и дискретны, а частота поставок находится в диапазоне 4 < G < 12, объемы поставок нормируемой марки материала (q) предприятию-потребителю будут постоянными и соответствовать транзитной норме отгрузки2. [c.357]
