Решение. Первый вариант помещения денег является постоянным аннуитетом постнумерандо, член которого равен 3 тыс. руб., срок - 7 лет, и период равен одному году. Изобразим схематично эту ситуацию на оси времени (одно деление равно одному году), помещая над осью члены аннуитета. [c.266]
Решение. Первый вариант оплаты представляет собой аннуитет постнумерандо при п 6 и А =20 тыс. руб. Схематично этот вариант можно представить таким образом [c.267]
Решение. Для ответа на поставленный вопрос во всех случаях необходимо определить приведенную стоимость аннуитета постнумерандо при А = 8 тыс. руб., и = 6. [c.271]
Решение. При нахождении искомой суммы во всех случаях необходимо определить приведенную стоимость -срочного аннуитета постнумерандо при /> = 4, А = 12/4 = 3 тыс. руб., п = 8. [c.271]
Решение. Выплаты работнику после выхода на пенсию представляют собой аннуитет постнумерандо с членом Л = 8000 руб. и длительностью и = 18 лет. Полагая г = 20%, по [c.276]
Решение. Денежный поток во всех случаях является бессрочным аннуитетом постнумерандо, причем А = 12 тыс. руб. Необходимо найти приведенную стоимость этого аннуитета. [c.279]
Решение. Так как поток годовых платежей представляет собой аннуитет постнумерандо, то срок и погашения долга можно определить, преобразовав формулу (121) [c.283]
Анализируются два варианта накопления средств по схеме аннуитета постнумерандо а) класть на депозит 30 тыс. руб. каждые полгода при условии, что банк начисляет 18% годовых с полугодовым начислением сложных процентов б) делать ежегодный вклад в размере 63 тыс. руб. на условиях 19% годовых при ежегодном начислении сложных процентов. Какая сумма будет на счете через 10 лет при реализации каждого плана Какой план более предпочтителен Изменится ли ваш выбор, если процентная ставка во втором плане будет снижена до 18,5% [c.285]
Имеется бессрочный аннуитет постнумерандо с ежегодными выплатами по 1 тыс. руб. Требуется определить приведенную стоимость этого аннуитета при годовой процентной ставке а) 5% б) 10% в) 100%. Как изменятся расчетные значения для аннуитета пренумерандо с такими же выплатами [c.290]
Определите текущую (приведенную) стоимость бессрочного аннуитета постнумерандо с ежегодным поступлением 4,2 тыс. руб., если предлагаемый государственным банком процент по срочным вкладам равен 24% годовых, причем сложные проценты начисляются по полугодиям. [c.290]
Имеет ли смысл говорить о непрерывном аннуитете как об аннуитете постнумерандо или пренумерандо [c.293]
Предполагая же, что в условии говорится о постоянном аннуитете постнумерандо или пренумерандо, соответственно по формулам (122) и (126) получим [c.295]
Решение, а) Согласно условию имеем переменный аннуитет постнумерандо с постоянным абсолютным изменением его членов и, следовательно, для оценки аннуитета воспользуемся формулами (140) и (141). По условиям соглашения А = 4 тыс. руб., и = 8, г = 0,2, и если суммы возрастают, то г = 0,5 тыс. руб. Поэтому [c.299]
Нетрудно получить формулы оценки аннуитета, аналогичные формулам (140), (141), и для других ситуаций. Однако эти формулы приобретают несколько громоздкий вид. Например, если в переменном аннуитете постнумерандо с постоянным абсолютным изменением его членов начисление сложных процентов происходит m раз за период, то можно показать, что [c.300]
Решение. Поскольку ежегодно платежи увеличиваются в 1,1 раза (на 10%), то денежный поток представляет собой переменный аннуитет постнумерандо с постоянным относительным изменением его членов. Поэтому для оценки аннуитета воспользуемся формулами (143) и (144). Полагая Л = 4 тыс. руб., п = 7, г = 0,28 и q = 1,1, получим [c.302]
Имеется переменный аннуитет постнумерандо (тыс. руб.) 14, 40, 25, 10. Рассчитайте а) будущую стоимость аннуитета б) приведенную стоимость аннуитета, если его период совпадает с базовым периодом начисления процентов по сложной процентной ставке 30% годовых, т.е. равен одному году. Как изменятся полученные оценки, если исходный поток представляет собой аннуитет пренумерандо [c.305]
Формулы для оценки будущей и приведенной стоимости аннуитета, период которого больше базового периода начисления процентов, аналогичны формулам для оценки будущей и приведенной стоимости обычного аннуитета. Формулы для оценок аннуитета пренумерандо получаются из соответствующих формул для оценок аннуитета постнумерандо с использованием, как правило, того факта, что денежные поступления пренумерандо начинаются на период (аннуитета) раньше, чем постнумерандо. [c.307]
Приведите формулу приведенной стоимости бессрочного аннуитета постнумерандо, период которого больше базового периода начисления процентов. [c.307]
Решение. Денежные поступления образуют постоянный аннуитет постнумерандо с А = 3 тыс. руб., сроком и = 12 лет и периодом и = 2 года. Следовательно, период аннуитета больше базового периода начисления процентов, равного году. Схематично это выглядит таким образом [c.308]
Будущая стоимость переменного аннуитета постнумерандо [c.335]
Оценка постоянного р -срочного аннуитета постнумерандо [c.336]
Оценка постоянного аннуитета постнумерандо в случае начисления непрерывных процентов [c.337]
Оценка переменного аннуитета постнумерандо, платежи которого образуют арифметическую прогрессию а) будущая стоимость аннуитета [c.339]
Оценка постоянного аннуитета постнумерандо, период которого больше базового периода начисления процентов [c.340]
Аннуитеты постнумерандо и пренумерандо. Примеры аннуитетов. [c.377]
Будущая и приведенная стоимости(аннуитет постнумерандо) [c.395]
В частности, для решения прямой задачи оценки срочных аннуитетов постнумерандо и пренумерандо при заданных величинах регулярного поступления (А) и процентной ставке (г) можно воспользоваться формулами (2.13) и (2.14) [c.75]
Для решения обратной задачи оценки срочных аннуитетов постнумерандо и пренумерандо, являющейся основной при анализе инвестиционных проектов, денежные притоки которых имеют вид аннуитетных поступлений, можно воспользоваться формулами (2.16) и (2.17) [c.75]
В этом случае прямая задача смысла не имеет. Что касается обратной задачи, то ее решение для аннуитета постнумерандо делается на основе формулы [c.154]
Привилегированные акции как и бессрочные облигации генерируют постоянный доход неопределенно долго, поэтому их текущая теоретическая стоимость определяется по формуле (11.18), применяемой для оценки приведенной стоимости бессрочного аннуитета постнумерандо. Таким образом, наиболее простым вариантом оценки привилегированной акции является отношение величины дивиденда к рыночной норме прибыли по акциям данного класса риска (например, ставке банковского процента по депозитам с поправкой на риск). [c.462]
Рассмотрим аннуитет постнумерандо с ежегодными платежами Р в течение лет, на которые начисляются проценты по сложной годовой ставке /с (рис. 5). [c.117]
| Рис. 5. Будущая стоимость аннуитета постнумерандо | 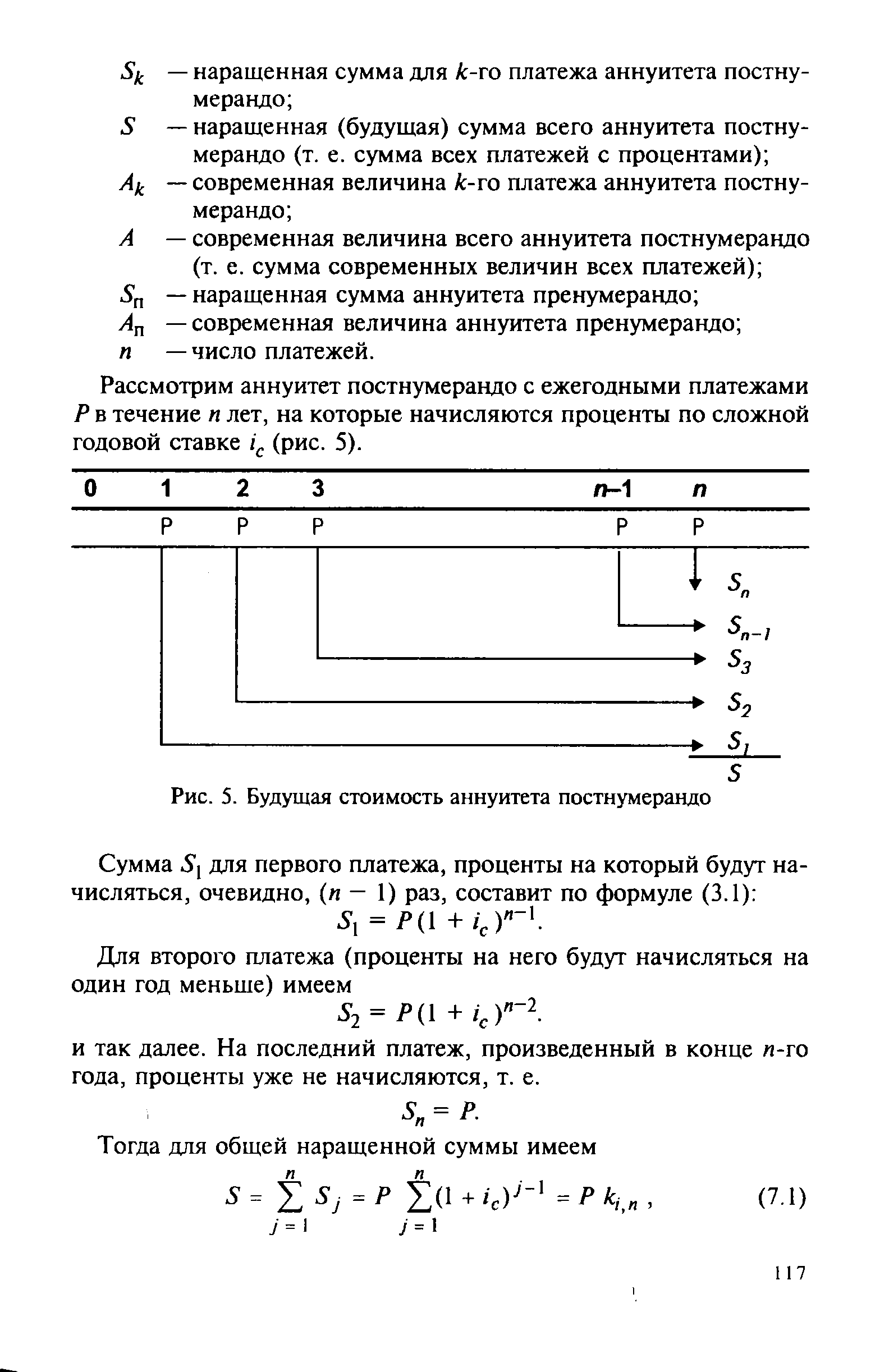 |
| Рис. 6. Современная величина аннуитета постнумерандо | 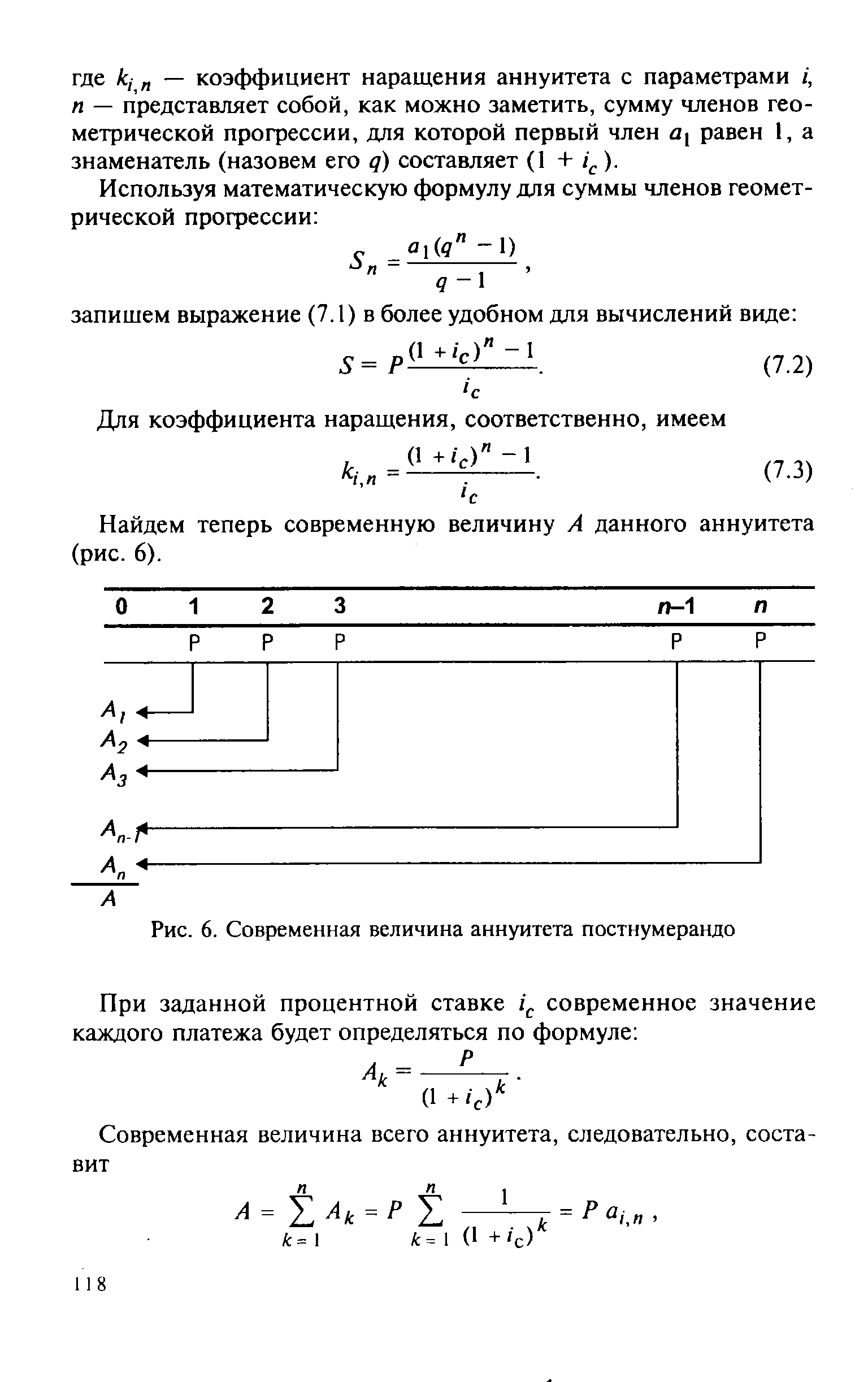 |
Если срок аннуитета п не ограничен, мы получаем случай вечного аннуитета. Для аннуитета постнумерандо выражения для наращенной суммы и современной величины приобретут следующий вид [c.121]
Рассмотрим схему, предполагающую погашение долга вместе с процентами равными суммами, выплачиваемыми в течение ряда периодов. Вносимая сумма получила название аннуитета.1 Различают аннуитеты постнумерандо (платеж производится в конце каждого периода) и пренумерандо (в начале периода). [c.632]
Аннуитет, или финансовая рента — однонаправленный денежный поток с равными временными интервалами. Любой элемент денежного потока называется членом аннуитета (членом ренты), а величина постоянного временного интервала между двумя его последовательными элементами называется периодом аннуитета (периодом ренты). Если каждый элемент аннуитета имеет место в конце соответствующего периода, аннуитет называется аннуитетом постнумерандо если в начале периода — аннуитетом пернумерандо. Аннуитет, все элементы которого равны между собой, называется постоянным если равенства нет, аннуитет носит название переменного. [c.296]
Аннуитет, для которого платежи осуществляются в начале соответствующих интервалов, носит название аннуитета пренуме-рандо если же платежи осуществляются в конце интервалов, мы получаем аннуитет постнумерандо (обыкновенный аннуитет) — пожалуй, самый распространенный случай. [c.116]
Так как первый платеж совпадает с моментом покупки, в данном случае размер платежа следует рассматривать как аннуитет пренуме-рандо формула (1) соответствует аннуитету постнумерандо, и для нашего расчета ее нужно несколько изменить. Поскольку все платежи сдвигаются на один период вперед, не повторяя рассуждений, можно утверждать, что величина каждого платежа уменьшится в (1 + г ) раз, так что [c.635]
