| Рис. 5. Бюджетная плоскость в трехмерном пространстве. | 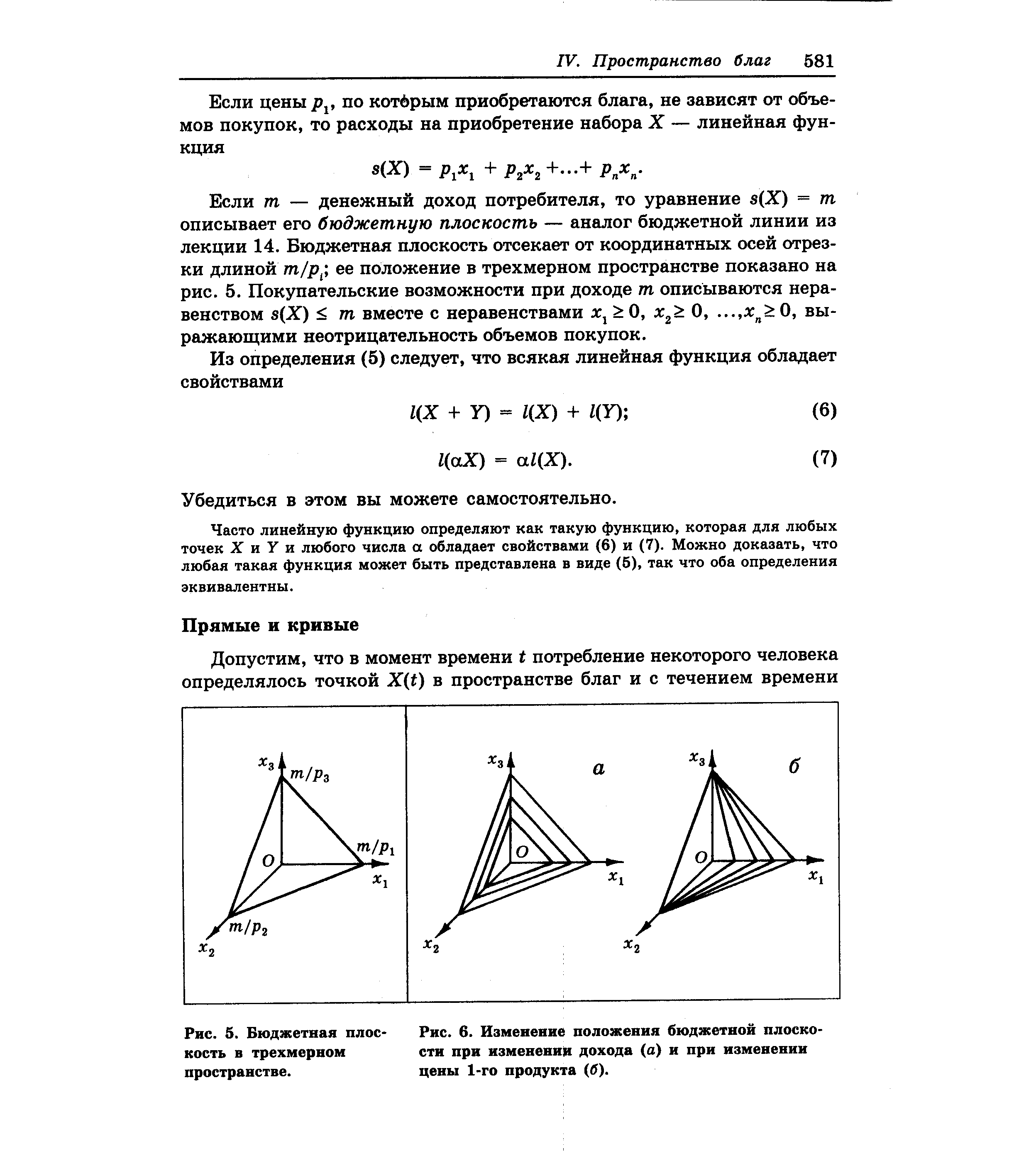 |
| Рис. 6. Изменение положения бюджетной плоскости при изменении дохода (а) и при изменении цены 1-го продукта (б). | 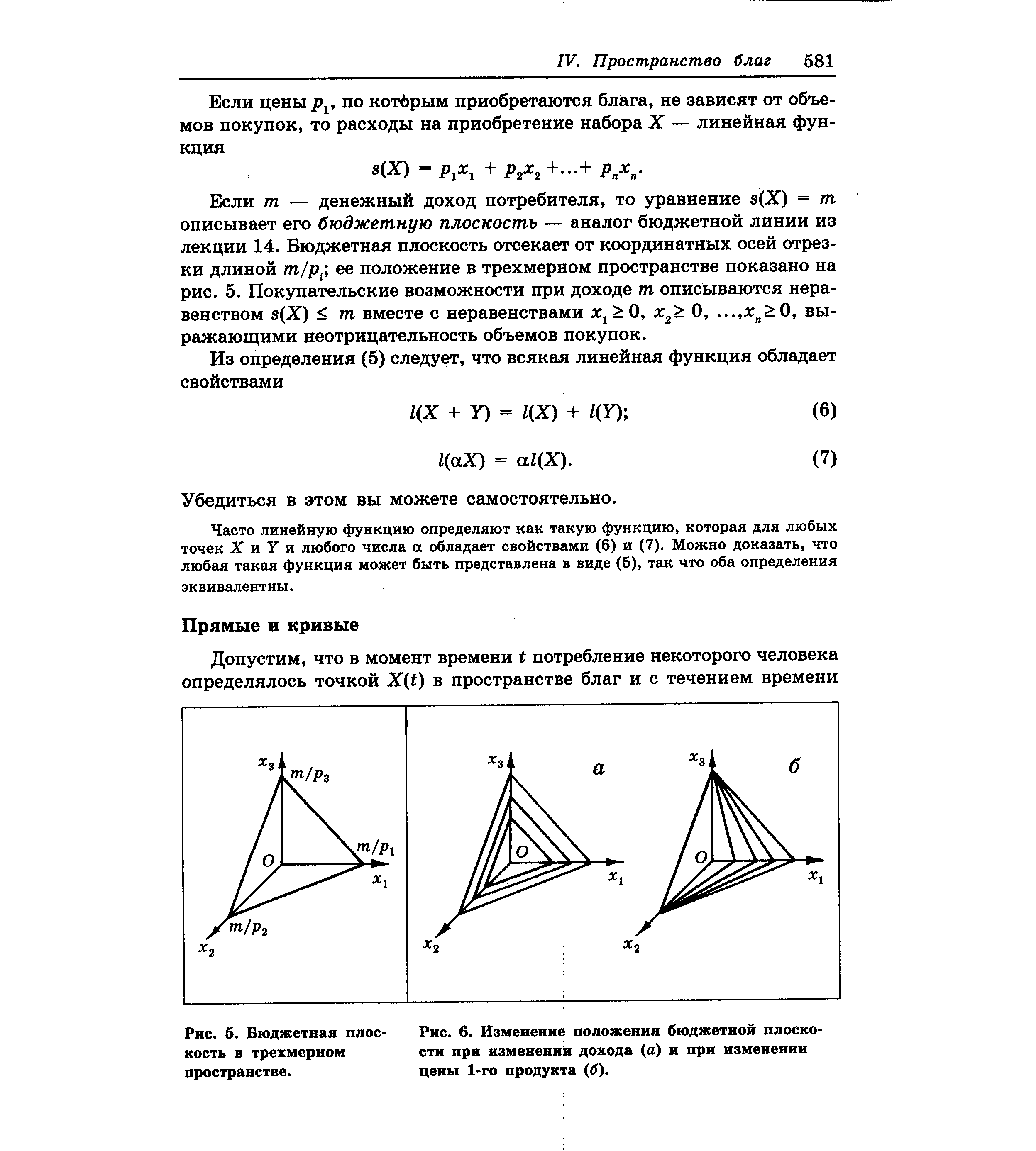 |
Бюджетная плоскость 2 248, 249 Бюджетное ограничение 1 194 2 69, [c.265]
| Рис. 5. Бюджетная плоскость Рис. 6. Изменение положения бюджетной плоскости в трехмерном пространстве при изменении дохода (а) и при изменении цены 1-го |  |
Выясним теперь смысл второго слагаемого уравнения (3.5). Для этого рассмотрим влияние компенсированного изменения цены р, т.е. такого изменения, при котором одновременно меняется капитал К так, чтобы максимальное значение функции полезности на соответствующей бюджетной плоскости оставалось неизменным. Иными словами, теперь мы предполагаем, что капитал К зависит от р, т.е. является [c.25]
Горизонтальная модель . Для бюджетной системы дореволюционной России типичной была модель распределения доходов между бюджетами, которую можно назвать горизонтальной. Государственный бюджет и территориальные бюджеты (земские, городские) находились как бы в одной плоскости, за каждым бюджетом были закреплены свои налоги и сборы. При этом финансовая помощь территориальным бюджетам из государственного бюджета была затруднена, так как территориальные бюджеты не входили в государственный бюджет и для такой помощи не было правовых основ. В этих условиях действовала следующая модель формирования территориальных бюджетов [c.127]
В отличие от ТЗР, прямых производственных и коммерческих расходов складские расходы относятся к категории косвенных затрат, то есть по ним планируется совокупная смета, а по окончании бюджетного периода производится распределение фактической величины складских расходов по видам сырья и материалов в соответствии с выбранной базой распределения. Распределение складских расходов производится в двух плоскостях [c.132]
Таким образом, в контексте управления предприятием вопрос изменения эффективности прямых коммерческих расходов и вопрос эффекта изменения величины ПКР на доход от продаж и рентабельность отдельных видов продукции лежат в разных плоскостях и влекут за собой различные управленческие меры. Эффективность ПКР касается функционирования подразделения, занятого отгрузкой продукции, и может обусловить такие мероприятия на следующий бюджетный период, как пересмотр норм удельных прямых коммерческих расходов, бюджета ПКР в целом, ужесточение системы контроля расходования материалов и рабочего времени и т.п. Следовательно, изменение эффективности ПКР определяет общее снижение величины прямых коммерческих расходов в себестоимости реализации всех продаваемых видов продукции. Эффект же пересмотра бюджета ПКР на изменение рентабельности отдельных изделий зависит не только от бюджета ПКР, но и от уровня отпускных цен. [c.365]
Представим эту ситуацию графически на плоскости ot l (рис. 1). Точка АО соответствует объемам потребления в обоих периодах, совпадающим с доходами в тех же периодах (т. е. без обращения потребителя к рынку заемных средств). Бюджетная линия KL — прямая, проходящая через точку А,, ее угловой коэффициент равен 1 + г. [c.135]
Пусть доход покупателя, авансированный на удовлетворение потребности, таков, что он может приобрести А = 1/Ра количество товара А и С = 1/Рс количество товара С, а также линейные комбинации этих наборов. Отрезок [А С ] - аналог бюджетной линии - носит название эффективной границы на плоскости характеристик. [c.116]
Для любых точек координатной плоскости, расположенных ниже бюджетной линии kl, комбинации набора единиц одежды и продуктов питания достижимы, если потребитель будет тратить свой бюджет Сь С2, С0 не полностью. [c.12]
Отметим, что уравнение (3.2) — это условие того, что бюджетная плоскость касается поверхности уровня функции полезности (градиент функции полезности сонаправлен с нормалью р к бюджетной плоскости). [c.24]
Поскольку карта безразличия представляет теперь плоскость характеристик, а не самих товаров, как это принято при традиционном подходе, существенному переформулированию подверглась структура бюджетного ограничения и ее интерпретация. [c.162]
Таким образом, точки А, В, С, D характеризуют на плоскости характеристик XOY максимум значимых для потребителя свойств X и У, которые он может получить, израсходовав всю ассигнованную сумму EXY на соответствующий товар А, В, С или D. Соединив эти точки, мы получим ломаную линию А В С D, которую называют эффективной границей на плоскости характеристик, соответствующую по своему значению бюджетной прямой при традиционном ординалист-ском подходе. [c.164]
Равновесие Линдаля иллюстрирует Рис. 90 ( диаграмма Кольма ). На рисунке изображена экономика с двумя благами, общественным (/с = 1) и частным (/с = 2), и двумя потребителями, в которой технология позволяет производить из единицы частного блага единицу общественного. Точки А, В и С соответствуют суммарным начальным запасам частного блага, Q22 = Q12 + Q22, отложенным по осям ж1 ж12 и ж22 соответственно. Они задают симплекс AB допустимых состояний экономики. Две дуги, показанные пунктиром, — это кривые безразличия потребителей в равновесии Линдаля в соответствующих системах координат. Их касаются бюджетные прямые потребителей, показанные штрих-пунктирными линиями. Все эти линии из систем координат потребителей 1 и 2 проецируются на плоскость AB параллельно осям ж22 и х12 соответственно. Проекции двух бюджетных прямых совпадают — это прямая, проходящая через точку начальных запасов со и через точку х равновесия Линдаля. В точке х две проекции кривых безразличия касаются друг друга (показаны сплошной линией). Касание проекций кривых безразличия говорит о Парето-оптимальности равновесия Линдаля. [c.419]
