Предположение (6.4) является естественным оно играет важную роль в теории этих функций и при их построении ). На основе этого свойства можно ввести понятие поверхности безразличия,. которая определяется как множество всех таких векторов у, для которых выполняется условие [c.117]
Поверхность безразличия — это множество наборов продуктов, которые имеют одинаковую ценность для потребителя. Выбирая различные значения постоянной с в выражении (6.6), можно построить семейство поверхностей безразличия. Это семейство характеризует свойства функции предпочтения, частично упорядочивая различные наборы продуктов. Точнее говоря, если некоторый набор г/А лежит на поверхности безразличия и(у) = СА, а набор ув лежит на поверхности безразличия и(у) = св, причем СА > св, то набор уА лучше набора ув. В том случае, когда оба набора находятся на одной поверхности (сл = св), эти наборы эквивалентны в смысле функции предпочтения и(у). [c.117]
Так как согласно сделанным предположениям потребитель выбирает такой вектор у, на котором достигается максимум функции предпочтения при выполнении ограничений (6.1), (6.2), то с точки зрения описания зависимости спроса от цен и дохода семейство (или, как принято говорить, карта) поверхностей безразличия содержит ту же информацию, что и функция предпочтения. В этом смысле карта поверхностей безразличия эквивалентна функции предпочтения, поэтому часто вместо построения функции предпочтения сразу строят семейство поверхностей безразличия. [c.117]
Конечно, все сказанное не означает, что описание предпочтений потребителя в виде функции предпочтения и описание в виде поверхностей безразличия полностью эквивалентны. Если функция предпочтения задает карту поверхностей безразличия однозначно, то относительно обратного перехода такое утверждение было бы неправильным. Действительно, как легко заметить, умножение функции предпочтения на какое-либо положительное число а к изменению карты безразличия не приводит, поскольку из и(уА) > и(ув) следует а,и(уА) > au(z/B), a из и(уА) = и(ув) следует аи(уА) = аи(ув). Более того, для любой монотонно возрастающей функции ф(ю) новая функция предпочтения и(у) = =
Рассмотрим карту поверхностей безразличия более подробно. Свойства этих поверхностей могут быть получены на основе соотношений (6.4). Будем для простоты считать, что функция полезности дифференцируема и имеет место соотношение [c.117]
Поэтому при движении вдоль поверхности безразличия предельные предпочтения гг,-(г/) (i = l,. . ., п) удовлетворяют [c.118]
Соотношение (6.8) показывает, что при изменении количеств только двух товаров, скажем /-го и k-io, на поверхности безразличия имеем [c.118]
В силу (6.7) эта величина отрицательна. Этот факт позволяет качественно представить вид поверхностей безразличия. [c.118]
Построение функций предпочтения. Некоторые конкретные виды функций предпочтения. Построение функций предпочтения (или семейства поверхностей безразличия) обычно основывается на изучении расходов потребителей на покупку товаров. Для этого все семьи разбивают на некоторое число групп, различающихся между собой структурой семьи (в том числе количеством человек в семье), а также традициями, социальным положением и т. д. Предполагается, что для каждого типа семей функция предпочтения одинакова. Для ее построения либо выбирают несколько типичных семей группы и анализируют их доходы и расходы, либо изучают доходы и расходы всех семей группы в целом. На основе полученной информации оценивают коэффициенты функций предпочтения, тип которых обычно определяется заранее из теоретических соображений. [c.120]
Поэтому согласно (6.8) уравнение поверхности безразличия имеет вид [c.121]
Отсюда получаем, что поверхность безразличия описывается соотношением [c.121]
Семейство поверхностей безразличия для двух товаров при [c.121]
Пусть вся продукция, выходящая за пределы производственной сферы народного хозяйства, описывается в модели с помощью вектора y = (j/i,. . ., j/n). Концепция ЦФП базируется на представлении о возможности соизмерения различных видов продукции и связанных с ними показателей в единой функции -U(y). Эта функция (ЦФП) должна показывать степень удовлетворения потребностей общества. Она является в некотором смысле обобщением понятия функции предпочтения, введенной ранее для одного индивидуума или одной семьи. Считается, что ЦФП должна обладать свойствами, близкими к свойствам функции предпочтения, т. е. она должна расти или по крайней мере не должна убывать при росте количества хотя бы одного товара (см. (6.4)-и (6.5)). Для ЦФП вводится понятие поверхности безразличия, строятся карты поверхности безразличия. [c.130]
Для рассмотрения всех возникающих при таком подходе к явлению вопросов теория предельной полезности, а вслед за ней и специальные маркетинговые исследования рынка потребителей привлекают функции спроса, кривые и поверхности безразличия, предпочтения, которые базируются на умозрительных построениях в рамках так называемого функционального подхода. Эти построения исходят из того, что при определенных рыночных ситуациях возникают некоторые универсальные характеристические соотношения между ценами и объемами одного и того же товара. [c.222]
Для уточнения понимания этой процедуры произведем необходимые аналитические преобразования для определения алгебраической формы кривых/поверхностей безразличия в избранном пространстве потребляемых благ. [c.233]
Осуществленный переход (11.4.6) дает в результате уравнение конической поверхности безразличия [c.233]
| Рис. 11.3. Поверхность безразличия и функции полезности (поверхность является конической). | 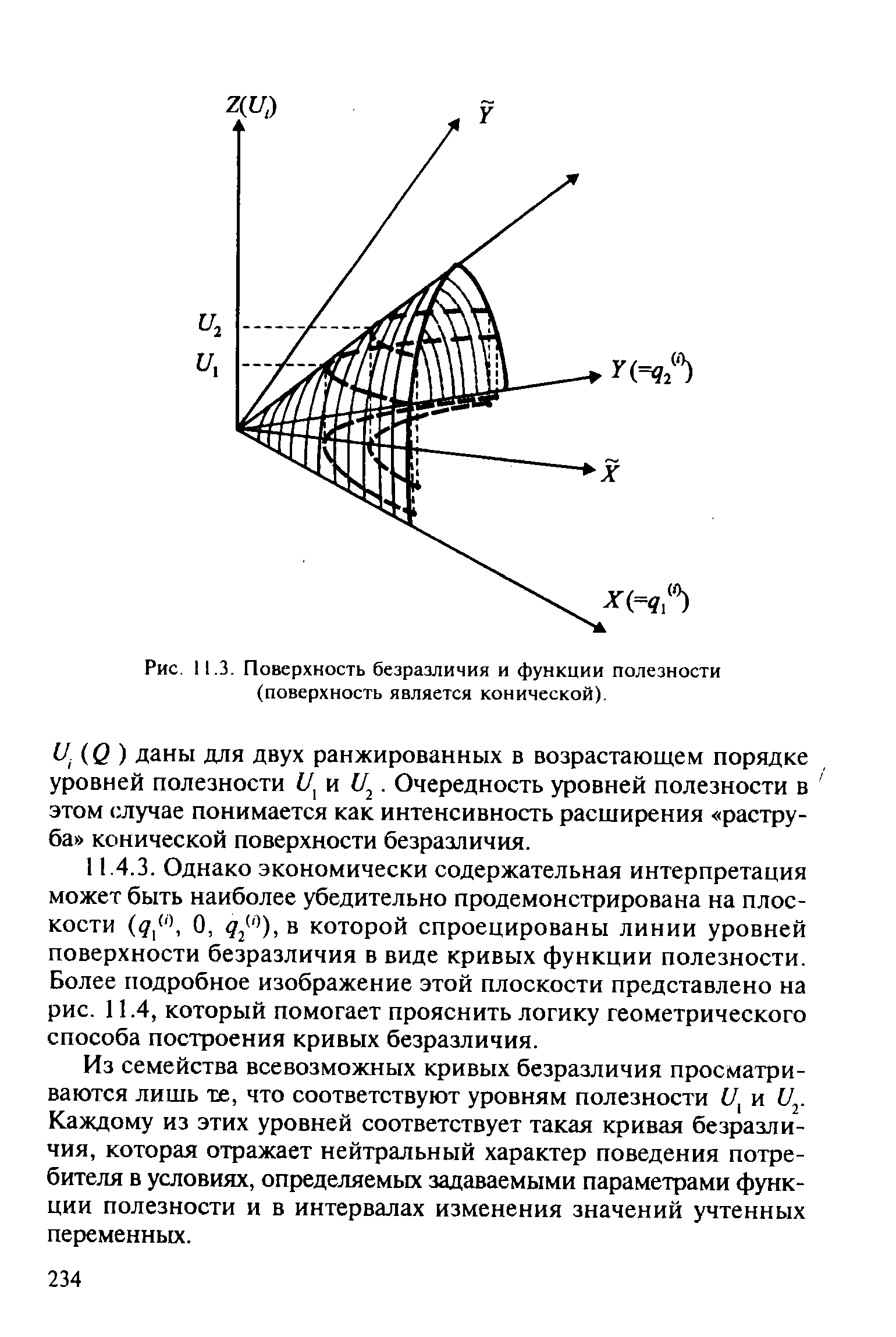 |
Однако экономически содержательная интерпретация может быть наиболее убедительно продемонстрирована на плоскости ( 1(0, 0, <72(1)), в которой спроецированы линии уровней поверхности безразличия в виде кривых функции полезности. Более подробное изображение этой плоскости представлено на рис. 11.4, который помогает прояснить логику геометрического способа построения кривых безразличия. [c.234]
Кривые и поверхности безразличия. С повышением уровня благосостояния семей линии общих расходов и потребительские наборы, находящиеся в точках равновесия, удаляются от начала системы координат. От начала системы координат удаляются и кривые безразличия. Чем дальше расположена кривая безразличия, тем более высокой потребительной ценности набора она соответствует. [c.238]
Таким образом, функция безразличия (общей полезности) определяет наборы одинаковой потребительной ценности, или полезности, с точки зрения компетентного (просвещенного) потребителя. На указанном рис. 11.4 функция безразличия задана в виде гиперболы, любая точка которой определяет набор равной полезности. Для двух товаров — это кривая безразличия, для т товаров — поверхность безразличия, которую обычно записывают в виде следующего выражения [c.239]
В пространстве потребительских благ уравнению U (Y) — С соответствует поверхность равноценных, или безразличных, наборов благ, которая называется поверхностью безразличия. В частности, если взять две группы товаров, например продукты питания (yi) и непродовольственные товары и услуги (у ), то уровни целевой функции потребления можно изобразить на плоскости в виде кривых безразличия, соответствующих различным значениям величины С. Вид таких кривых представлен на рис. 25.5, где С < С < Сз. Термин кривые безразличия часто используется вне зависимости от размерности пространства потребительских благ и от количества групп товаров и услуг. [c.549]
Множество точек, в которых функция принимает одно и то же значение ф (X) = а, называют поверхностью уровня функции. Поверхность уровня разделяет пространство на две части, в одной из которых Ф (X) < а, а в другой ф (X) > а. Если, например, функция ф (X) описывает количественную полезность наборов, то поверхность уровня содержит такие наборы, полезность которых равна одной и той же величине, т. е. она является поверхностью безразличия (в кардиналистском смысле). Позже мы обсудим свойства поверхностей безразличия, отказавшись от количественного представления полезности. [c.580]
Существование функции полезности позволяет утверждать, что множество безразличия — это множество, удовлетворяющее уравнению ц(Х) = с, где с — константа. Иными словами, множество безразличия — это поверхность уровня функции полезности. Поэтому в дальнейшем мы с полным правом можем говорить о поверхности безразличия. [c.585]
Возьмем теперь в пространстве благ какую-либо поверхность безразличия и точку С на ней. Пусть U > С W.V > С, а точка X расположена на отрезке UV. Тогда обязательно имеет место отношение X > С — ведь наихудшая точка отрезка UV — это U или V. [c.587]
Таким образом, если U и V принадлежат множеству точек, не уступающих точкам данной поверхности безразличия, то и весь отрезок UV также принадлежит этому множеству. А это означает, что закон убывающей предельной полезности в пространстве благ любой размерности выглядит точно так же, как и в пространстве двух благ множество наборов, не менее предпочтительных, чем лежащие на данной поверхности безразличия, выпукло. [c.587]
Отметим, что выражение в левой части — это норма замещения i-того блага у -тым при постоянстве объемов всех остальных благ в пределах поверхности безразличия должно выполняться равенство [c.600]
Идейно, данное свойство функции полезности получается в предположениях достаточной гладкости поверхности безразличия, получаемой на основании наших предпочтений. [c.61]
В микроэкономике часто характеризуют предпочтения экономического агента кривыми (поверхностями) безразличия. Каждая из них выделяет множество одинаково предпочтительных состояний. Получение ЭА некоторого количества базисного или иного ресурса без изменения запасов остальных переводит его состояние на более высокую кривую безразличия, оно становится предпочтительнее. В работе [130] существование S было доказано, исходя из аксиомы Билля [180], использующей понятие предпочтения экономического агента в пространстве состояний X = (TV, М) ЭА не существует такой последовательности состояний XijXz,. ..,Хт, что Xi предподчтительнее, чем Xa- i для г = 2,. ..,т, а конечное и начальное состояния совпадают, Х — Хт. [c.220]
С помощью математического анализа будет показано, что отношение между комплементарностью и эластичностью по доходу (у независимых товаров) относится не только к знаку, но также и к величине. Если три товара независимые, то их эластичности по доходу зависят от их комплементарностей.41 Это можно легко показать на трехмерной диаграмме безразличия в следующей форме если дана одна поверхность безразличия, то могут быть введены все остальные поверхности безразличия. [c.141]
Следует подчеркнуть, что поверхности безразличия, в отличие от мер удовольствия, объективны и могут определяться эмпирически. Одно интересное экспериментальное исследование этой проблемы было проведено Л. Л. Тэрстоуном, который посредством анкетирования группы девушек добился успеха, опыт- [c.149]
Так как 2 PiQi — т, это значит, что Pfli т> то есть> что Q находится на той же гиперплоскости, на которой Q находилось в первом случае. Но поскольку Q было выбрано как точка на этой гиперплоскости, лежащая на поверхности безразличия, как можно более удаленной от центра, для которой Ф максимальна, и поскольку мы отбрасываем бесконечно неправдоподобный случай существования других точек на гиперплоскости, обладающих этим важнейшим свойством, следует, что Q должно лежать на какой-нибудь другой поверхности безразличия, и что это будет соответствовать меньшей степени удовлетворения. [c.154]
Смотреть страницы где упоминается термин Поверхность безразличия
: [c.118] [c.118] [c.118] [c.121] [c.392] [c.760] [c.268] [c.268] [c.248] [c.149] [c.150] [c.154] [c.453]50 лекций по микроэкономике Том 2 (2000) -- [ c.2 , c.580 , c.587 ]
