| Рис. 8. Унимодальная функция риска | 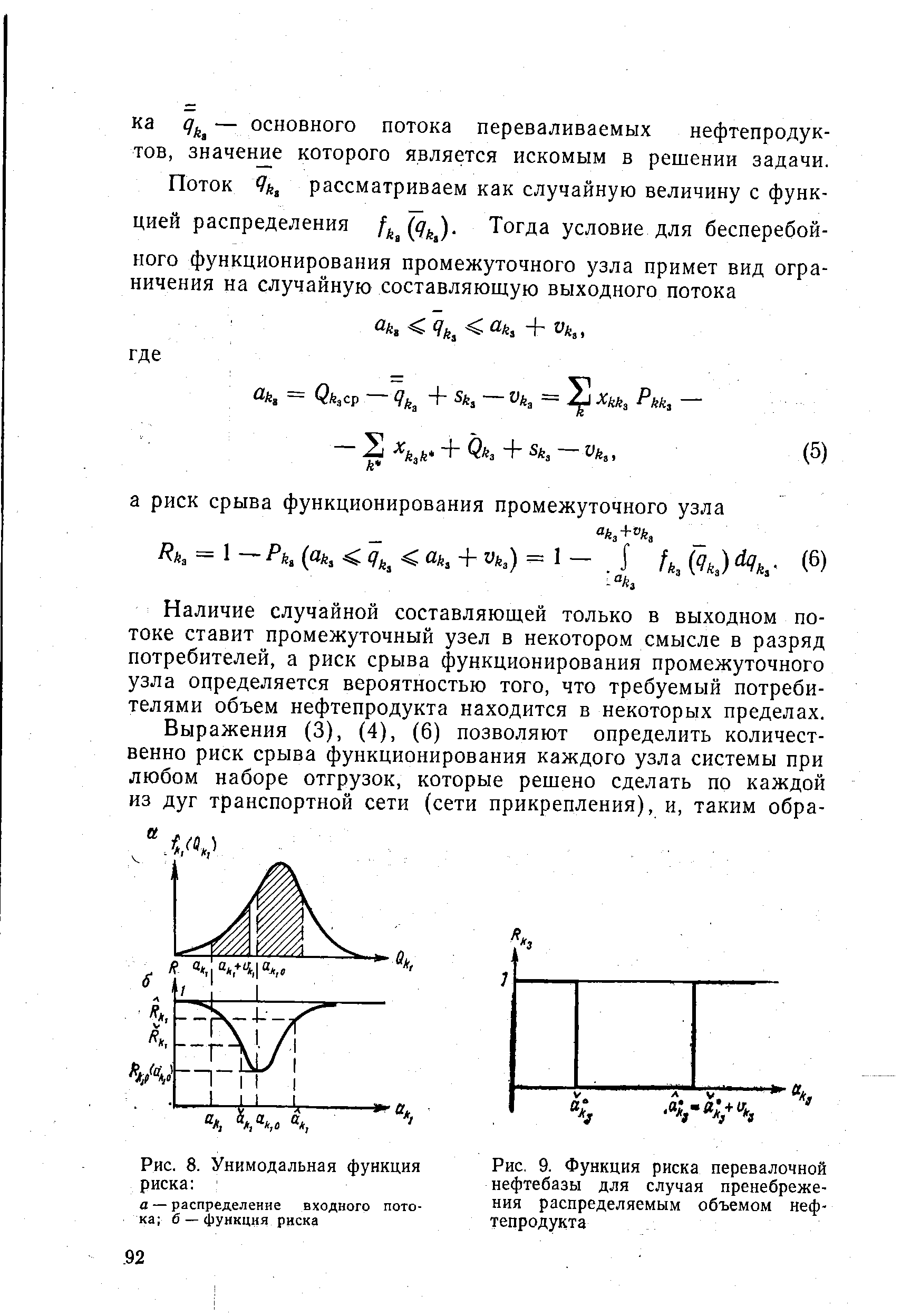 |
В-3-1. Область допустимых решений определена унимодальной функцией принадлежности. [c.85]
Однако теперь обе задачи — найти у и решить задачу (3) — существенно осложняются. Начнем с задачи (3). Для ее решения разработаны алгоритмы последовательных испытаний, т.е. вычислений <р (s) в некоторых специально выбираемых точках sk, имеющие целью локализацию точки минимума ценой наименьшего числа испытаний. Но эти алгоритмы работают только при определенных предположениях, Пусть ищется минимум функции
Покажем, что, несмотря на отличия модели для сети без циклов с промежуточными звеньями от модели для сети Кенига, решения задачи в обоих случаях единственны и алгоритмы их решений совпадают, если функция риска для промежуточных узлов также унимодальная. Если же функция риска для промежуточного узла имеет вид, представленный на рис. 9 или рис. 10, то решение может быть не единственным и в модель необходимо ввести дополнительные условия, как это сделано для сети Кенига, когда некоторые узлы-поставщики или узлы-потребители имели функцию риска вида, показанного на рис. 10. [c.150]
Наконец, в состоянии 7 (см. рис. 22) оказывается выполненным многопродуктовое ограничение а 1 + а 2 = Ну и задача решена. В рассмотренном примере функции риска во всех узлах каждой однопродуктовой сети предполагались унимодальными, а сами сети — без циклов. [c.168]
Понятие мода в статистике означает значение исследуемого признака, встречающееся в наибольшем числе случаев. Распределение предпочтений на рис. 3 является унимодальным, т.е. имеет одну моду Q (иначе говоря, график функции распределения предпочтений имеет один локальный максимум в точке Q ). Графи к на рис. 4, напротив, имеет два локальных максимума. [c.698]
Данное обстоятельство имеет значение, если выигрыш партии (например, число полученных мест в парламенте) пропорционален числу полученных голосов. Если же действует принцип победитель получает все (например, при выборе конкретного кандидата на место в парламенте или президентский пост), многое зависит от конкретной процедуры голосования (выборы в один или два тура, количество голосов, необходимых для победы, и т.д.). Однако правило об ориентации на модальную позицию сохраняет силу (равно как и в случае, когда распределение предпочтений избирателей является унимодальным, но асимметричным). В более общем случае - при полимодальном распределении предпочтений избирателей — за поддержку избирателей будут конкурировать столько партий, сколько локальных максимумов имеет функция распределения предпочтений членов общества. [c.698]
В дальнейшем будем считать, что функции риска для узлов-поставщиков и потребителей унимодальны и имеют минимум при единственном значении аьо параметра ah. И, как следствие, будем считать, что имеется единственное значение < м суммарных отгрузок от узла-поставщика и единственное значение Qk2o суммарных доставок нефтепродукта узлу-потребителю, минимизирующие риск срыва функционирования узлов. Случаи, когда функции риска имеют минимум не при одном значении ah, будут оговорены и рассмотрены особо. [c.96]
Суть алгоритма решения многопродуктовой задачи рассмотрим на простейшем примере двухпродуктовой задачи, такой, что каждая составляющая сеть однопродуктовой задачи не имеет циклов. Будем также считать, что функции рисков во всех узлах унимодальны, а ограничение по вывозу (завозу) суммарных объемов обоих нефтепродуктов наложено только на один узел k . Для узла k, на который наложено многопродуктовое ограничение [c.164]
Для оценки трех основных классов кривых (амодальных возрастающих, амодальных убывающих, унимодальных), определяющих функции принадлежности качественных характеристических параметров и предписаний, аналитические зависимости которых приведены в [171], целесообразно использование комбинированного показателя [c.77]
Функции принадлежности критериев, ограничений и управлений представляются в виде унимодальных и амодаль-ных кривых. Определение используемых значений функции принадлежности осуществляется с помощью приведенных в гл. 3 правил Д-1—Д-4. [c.122]
Преимущество такого способа определения F состоит в том, что при монотонных преобразованиях вид функции принадлежности меняется не кардинально. Ее унимодальность или монотонность сохраняется, и переход от нового вида функции к словесной оценке, соответствующей некоторому квантификатору, происходит куда проще, чем от многогорбых функций, возникающих в результате операции суперпозиции. [c.145]
Произведем гипотетический эксперимент. Оценим вид функции распределения р( ), производя вариацию всех параметров вектора К. При этом зададимся критерием правдоподобия нашего распределения — унимодальной гладкой функцией без изломов и разрывов (например, квадратичной многомерной параболой) - и пронормируем значение критерия. Например, если максимум правдоподобия имеет значение L, то вектор [c.36]
