| Рис.1. Классификация методов формализации экономических задач с учетом риска и неопределенности на основе диаграммы Эйлера-Венна. | 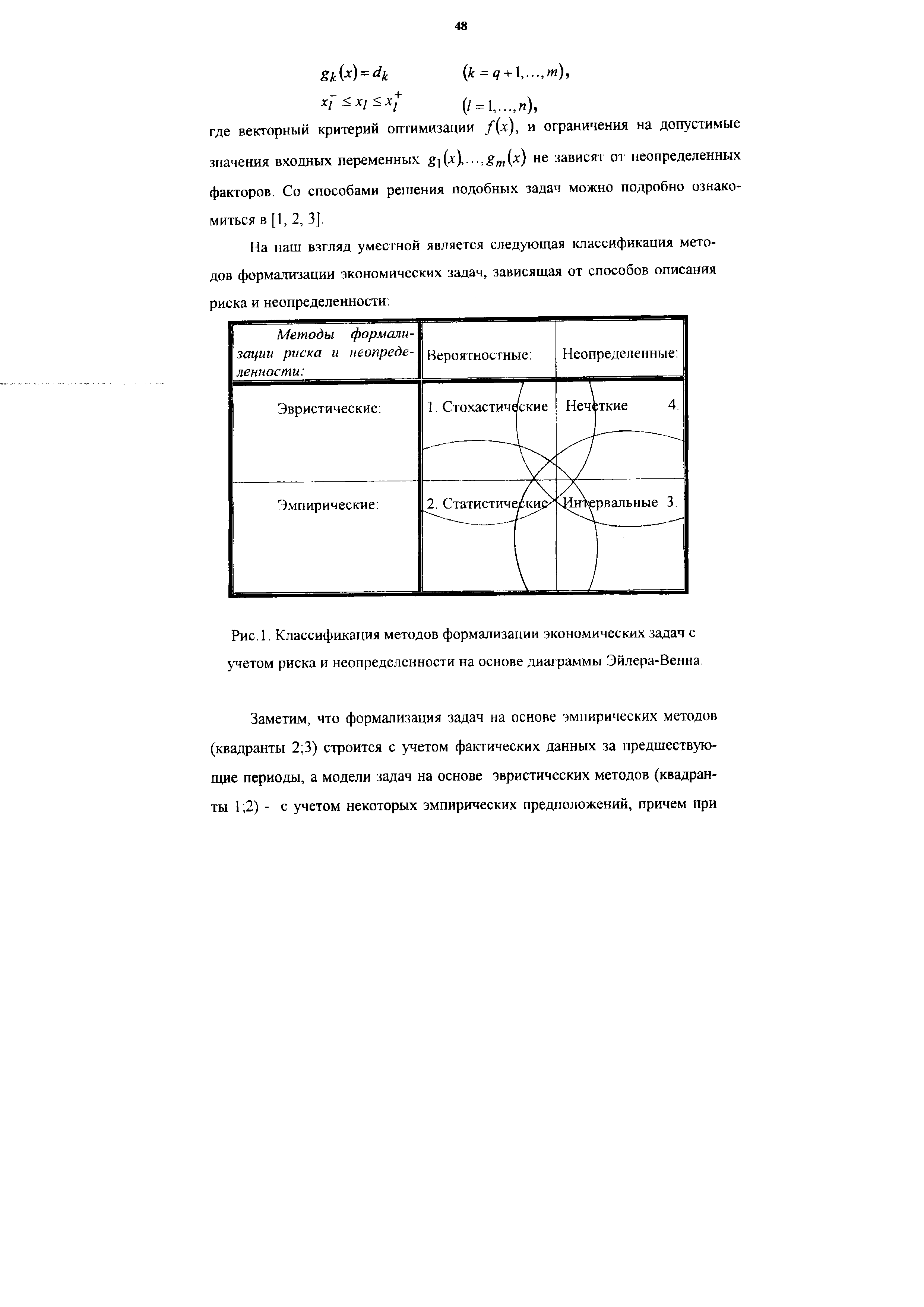 |
Для определения нагрузок от воздействия ленты на шкив трения используется известное зависимость Эйлера. В том числе стальная лента заменяется гибкой нитью, а шкив трение считается абсолютно жестким [1] На самом деле в зоне обхвата шкива лента работает и на растяжение, и на изгиб, а поверхность ленты покрыта системой колодок, способных работать на сдвиг. В работах [2] рассмотрен процесс передачи окружного усилия подъемным канатом в частности, изучено влияние изгибной жесткости каната на взаимодействие между канатом и абсолютно жестким шкивом. [c.92]
Интегральный метод дает наиболее общий подход к решению задач факторного анализа по разложению общего прироста показателя по факторным приращениям. В основе интегрального метода лежит интеграл Эйлера — Лагранжа, устанавливающий связь между приращением функции и приращением факторных признаков. Для функции z = (x, у) имеем следующие формулы расчета факторных влияний. [c.275]
Критическая сила (по Эйлеру) [c.230]
Из уравнения Эйлера в цилиндрических координатах для сплошной среды следует [c.23]
Равенство получено из уравнения Эйлера в цилиндрических координатах для сплошной среды без учета сил трения. [c.174]
Таким образом, инновации можно представить в виде диаграммы Эйлера-Венна, где пересекающимися множествами являются множества [c.66]
Объясните, что означают на диаграмме Эйлера-Венна участки с разной штриховкой [c.85]
ПРИЛОЖЕНИЕ 2.1. Гамма-функция Эйлера. [c.51]
Доход, остающийся в распоряжении фирм после того, как они оплатили расходы на все производственные ресурсы, называется экономической прибылью собственников фирм. Теорема об "исчерпании" устанавливает правила распределения доходов на совершенно конкурентных рынках. Она гласит, что если владельцы производственных ресурсов получают плату от фирмы за их использование, в точности равную предельному продукту этих ресурсов, то экономическая прибыль равна нулю (если предположить, что производственная функция обладает свойством постоянной отдачи от масштаба). Это неожиданное заключение следует из знаменитой теоремы Эйлера, которая утверждает, что если производственная функция F(K,L) (где К — капитал, L — труд) имеет постоянную отдачу от масштаба, то общую величину (или стоимость) выпуска можно разложить по составляющим затрат труда и капитала [c.242]
Проведем усреднение по времени Т г (г — эйлеров масштаб). Исправляя замеченные неточности в [Галкин, 1980 Галкин и др., 1981], проинтегрируем (2.4.6) по времени от t до [c.114]
В таблице использованы следующие обозначения Г(а) — гамма-функция - постоянная Эйлера. [c.32]
Обозначением числа е и его широким применением во многих вопросах математики мы обязаны Эйлеру. Это число иррационально и с точностью до шестой значащей цифры равно 2,71828 [c.86]
Российской Академией наук учреждена золотая медаль имени Эйлера. [c.87]
Эйлера, которая для данного примера имеет вид t — = V7x-lQ-x2 /(x - 2). [c.219]
Теорема (Эйлера). Если функция F(x, х -, , хп] есть однородная функция k-u степени, то [c.341]
Из теоремы Эйлера следует, что для линейно-однородной функции (k = 1) Кобба-Дугласа выполняется соотношение [c.341]
Хотя теорема Эйлера (37) имеет место для обеих моделей, роль ее в модели (33 ) — (37 ) оказывается несколько иной, нежели в модели (33) — (37). Определяемая ею тенденция к статическому равновесию остается в модели (33 ) — (37 ) лишь тенденцией само равновесие может не достигаться ни в одной точке развития, и только попадание на золотую магистраль обеспечивает равновесный рост. Долгосрочные цели (или долгосрочные ограничения) роста, отраженные в гипотезе о том, что норма накопления — независимый параметр развития, полностью подчиняют себе тенденции, связанные со стремлением к мгновенному оптимуму в смысле достижения максимальной прибыли в данный момент времени. Модель (33) — (37) превращает статическое равновесие в динамическое, причем не использует для этого какие-либо дополнительные гипотезы о цели роста. [c.66]
Руков. Гаджиев Эйлер Алиевич [c.404]
Процесс выполнения такой программы заключается в вычислении по значениям величин, характеризующих динамический процесс в предыдущий момент времени, новых значений этих величин, в последующий момент времени. Другими словами, в системной динамике способ имитации основан на процессе численного интегрирования систем обыкновенных дифференциальных уравнений по схеме Эйлера, подразумевающей разбиение отрезка интегрирования (моделирования) на интервалы одинаковой длины. При этом интервал должен быть меньше любого запаздывания (задержки во времени) в моделируемой системе. Таким образом, переменный уровень аппроксимируется кусочно-линейной функцией, т.е. считается, что между соседними точками уровень изменяется по линейному закону. [c.336]
Пусть решению С задачи Л° соответствует набор функций веса Р°М0,ъ). Уравнения Эйлера — необходимые условия, которым удовлетворяют функции . , [определяющие решение задачи А°, — имеют вид [c.329]
В конечном итоге сложилась концепция оптимальности макроэкономики. Она, по всей видимости, подтвердила известное высказывание Л.Эйлера о том, что в мире не происходит ничего, в чем не был бы виден смысл какого-нибудь максимума или минимума . Ориентация на экономико-математическое моделирование при анализе проблемы экономического оптимума в настоящее время стала преобладающей. [c.324]
Об однородных производственных функциях и об уравнении Эйлера см. Математическое приложение VII [c.182]
Линейно однородная функция удовлетворяет уравнению Эйлера [c.182]
Однородная функция степени а удовлетворяет уравнению Эйлера [c.608]
Разделив обе части уравнения Эйлера на f, получим [c.608]
К этому же утверждению приводит допущение о том, что производственная функция является однородной функцией первой степени, или линейно однородной, и потому удовлетворяет уравнению Эйлера [c.645]
В конце XVIII в. Л. Эйлер рассчитал, что период удвоения населения составляет 12,5 лет. Хотя эти темпы превышают рост населения любой страны, теоретические соображения Л. Эйлера были очень важны для развития прогнозирования. [c.59]
ЗИЛ ЕР (Euler) Леонард (1 707-1 783) — математик, механик и физик. Родился в Базеле, в Швейцарии, и учился там у Иоганна Бернулли. Он был членом Академий в Берлине и в Санкт-Петербурге, и прожил в России в совокупности 31 год. Был похоронен в Петербурге, оставив своей второй родине, наряду с выдающимися трудами, многочисленных потомков, представители которых носят и сегодня славную фамилию Эйлер в Петербурге и в Москве. [c.87]
Одной из отличительных сторон творчества Эйлера является его исключительная продуктивность. За первые 50 лет издательской деятельности Российской Академии наук (с 1729 до 1780 г.) Эйлеру принадлежит 60% всех ее публикаций по чистой и прикладной математике. Последние 13 лет жизни он работал в полной слепоте, диктуя свои работы ученикам. В его трудах многие математические формулы и символика впервые получают современный вид (например, ему принадлежат обозначения для е и тг). Сфера научных интересов Эйлера всеобъемлюща его труды — это энциклопедия точных наук XVIII века. Свыше 800 его научных работ составят 72 больших тома все еще незавершенного Полного собрания трудов , издаваемого в Швейцарии с 1911 г. [c.87]
XVIII и XIX веках. В XVIII веке в работах Л. Эйлера были найдены практически все известные в настоящее время приемы [c.222]
Применим для вычисления полученных сумм формулу Эйлера — Макло-рена [3], сохранив в ней лишь главный член, [c.178]
В 1736 г. по решению Сената была образована Комиссия весов и мер под председательством главного директора Монетного двора графа М.Г. Головкина. В состав комиссии входил Л. Эйлер. В качестве исходных мер длины комиссия изготовила медный аршин и деревянную сажень, за меру жидких веществ было принято ведро московского Каменномостского питейного двора. Важнейшим шагом, подытожившим работу комисии, было создание русского эталонного фунта. Работы начались в 1736 г. и завершились в 1747 г. изготовлением бронзовой золоченой гири, узаконенной в качестве первичного образца (государственного эталона) русских мер веса. Этот фунт почти 100 лет оставался единственным эталоном в стране. [c.7]
А как же решается проблема исчерпаемости для фирмы Подход, который был использован применительно к экономике в целом, для фирмы не подходит объем выпуска фирмы в общем случае не пропорционален затратам ресурсов. Но при определенных условиях предельные продукты факторов и их общий продукт связаны соотношением, аналогичным уравнению Эйлера. Эти условия выполняются, если и рынок продукта фирмы, и рынки, на которых она покупает факторы, находятся в состоянии конкурентного равновесия длительного периода. Более строгая формулировка и доказательство приведенного утверждения даются в Математическом приложении XIII. [c.182]
