Достаточно точное интегрирование такого уравнения методом второго, например, порядка точности (в наших расчетах использовался метод Эйлера с пересчетом) требует шага t 0,001. Поэтому шаг интегрирования дифференциальных уравнений (как прямого (1), так и сопряженных) не совпадал с шагом сетки для и (его величина Д 0,01), а был в 10 раз меньшим. Что касается числа S, то вначале оно задавалось величиной 100, а затем в процессе решения изменялось так, чтобы среднее значение м( ) было порядка 20. [c.259]
Каждый параметр, значения которого задаются подсистемой моделирования, имеет атрибут алгоритм интегрирования, определяющий метод численного приближенного решения обыкновенных дифференциальных уравнений. В системе G2 для этих целей используют методы Эйлера и Рунге - Кутта. Выбор среди этих двух методов зависит от приложения. [c.290]
Метод Рунге - Кутта дает более точные результаты, но требует в четыре раза больших затрат времени, чем метод Эйлера. Чтобы достигнуть той же точности, как в методе Рунге - Кутта, при использовании метода Эйлера необходимо значительно уменьшить время приращения. Таким образом, для приложений, которые требуют высокой точности и не предъявляют особых требований к скорости, часто эффективнее бывает использовать метод Рунге - Кутта. С другой стороны, для приложений, в которых существенна скорость, а не точность, целесообразнее применять метод Эйлера. [c.290]
Устойчивость (сходимость) метода не является фактором, на основании которого следует выбирать тот или иной метод, так как и метод Эйлера, и метод Рунге - Кутта имеют один и тот же предел [c.290]
Выбрав достаточно малый шаг приращения Л, построим систему равноотстоящих точек tt =to + ih (i = О, 1,2,. ..). Тогда в соответствии с методом Эйлера приближенные численные значения х( i, ) = х i вычисляются по формулам [c.291]
При этом С7 = <т(Г) + b. Для того, чтобы ее квадратичной форма была отрицательно определена, возьмем r(T)s-b-4. Задача решалась со следующими параметрами 6 = 10, Т = 4, отрезок интегрирования был разбит на 200 участков. Для интегрирования использовался метод Эйлера. Решение было получено за 6 итераций. Пример 2. [c.288]
| Рис.1. Классификация методов формализации экономических задач с учетом риска и неопределенности на основе диаграммы Эйлера-Венна. | 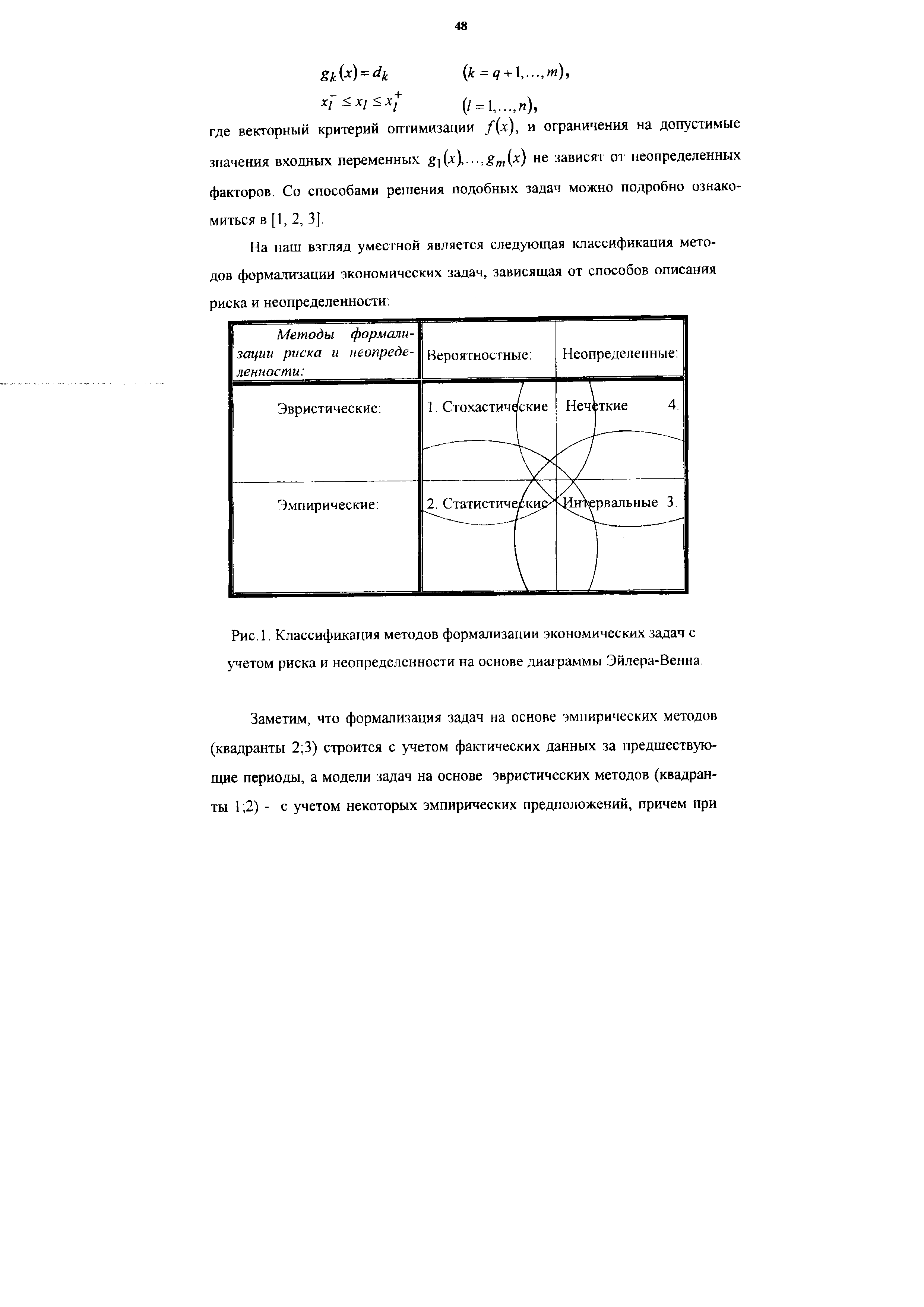 |
Выбор начального приближения. Модификация метода Ньютона не снимает проблемы подбора достаточно хорошего начального приближения, хотя и заметно ослабляет остроту этого вопроса. Опыт показал, что использование каких-либо содержательных соображений в целях нахождения хорошего начального приближения 1° крайне затруднительно даже в тех задачах, где подбор разумного приближения в терминах управляющей функции и (t) сравнительно прост. Пожалуй, единственным выходом является решение задачи каким-либо иным методом, достаточно надежно дающим относительно грубое приближенное решение. Такие приближенные методы в настоящее время разработаны, отличительной их чертой является то. что они дают хорошее приближение к искомому решению с точки зрения фазовой траектории х (t) и значений функционалов задачи Ff [и ( )], однако обычно довольно грубое с точки зрения управляющей функции и (t). Фигурирующий в принципе максимума вектор g тоже, как правило, получается с хорошей точностью. Создание приближенного метода решения задач оптимального управления, соединяющего надежность и эффективность с хорошей точностью по всем компонентам задачи возможно, видимо, лишь комбинированием методов грубого поиска минимума с последующим уточнением точного вида решения, основанным на использовании характеризующих его уравнений типа принципа максимума или уравнения Эйлера. [c.120]
Пятое предположение плохая сходимость метода спуска по градиенту связана с тем, что градиент вычисляется применением к исходному приближению х° (t) неограниченного оператора Эйлера, эквивалентного, грубо говоря, оператору d /dt2 умножение его на положительную функцию типа (8) приводит к такому же, в сущности, оператору t (Т — t) d /dt2 и не решает проблемы. Попробуем умножить градиент на положительный оператор, который в основной своей дифференциальной части был бы обра-тен оператору Эйлера. Так приходим к направлению спуска [c.222]
Какой бы метод ни применялся, из теоремы Эйлера видно, что в условиях, когда физическая отдача в некотором смысле постоянна, прибыль должна быть равна нулю. Если конкуренция совершенна, то заработок каждого фактора равен ценности его предельного физического продукта, а на долю работодателя не остается ничего. [c.70]
Полная гармония между ними наглядно проиллюстрирована в случае, когда фирма, работающая на несовершенном рынке, оказывается в условиях постоянной физической отдачи. Это произойдет, если по счастливой случайности кривая предельной выручки пересечет кривую предельных затрат в точке объема выпуска, в которой последняя пересекает кривую средних затрат. Итак, имеет место постоянная физическая отдача, но факторы получают меньше своего предельного продукта в результате прибыль положительна. Факторы получают соразмерно стоимости своего предельного продукта, но будет иметь место убывающая отдача, выраженная в ценностной мере в результате прибыль положительна. При любых методах доказательства положения теоремы Эйлера оказываются выполнимыми. [c.77]
В полученных решениях не удалось дать общих методов исследования подобных задач. Они были построены спустя пятьдесят лет учеником Иоганна Бернулли Леонардом Эйлером, заложившим основы современного вариационного исчисления. [c.17]
С этими же трудностями связано возвращение к методу Эйлера в его самой бесхитростной форме. Имеется в виду то направление, которое получило название метод математического программирования в теории оптимального управления . Почти всякий метод приближенного решения задач оптимального управления может быть охвачен этим термином, поэтому следует уточнить, о чем идет речь. Это — направление, в котором задачу заменяют конечно-разностной, переписывают все ограничения задачи в виде ограничений на значения сеточных функций, интегралы заменяют суммами, и, получив конечномерную задачу минимизации при наличии ограничений, ссылаются на возможность ее решения хорошо разработанными методами математического программирования. Последние представляют тему огромного числа статей и монографий, но это как раз и свидетельствует о том, что надежных методов решения общей задачи минимизации нет. [c.112]
Одним из простейших разностйыж методов является метод ломаных или метод Эйлера. [c.169]
Эти соображения позволяют оценить и длину шага интегрирования на отрезке [0 Т]. При достаточно больших 1(0 процессы, получаемые с помощью этого алгоритма могут иметь вырожденные участки ( псевдоскользящие режимы ), объясняемые не структурой задачи, а параметрами численного метода. Возникают они в том случае, когда выбор новой программы управления u(t,x) целиком определяется поведением ЕДх. Рассмотрим это явление, предполагая что для интегрирования используется метод Эйлера. [c.293]
Основные типы задач, подходы к их решению и результаты были получены давно они связаны с именами таких классиков естествознания, как Эйлер, Якоби, Вейерштрасс. Однако бурное развитие техники ) после второй мировой войны, характеризующееся, кроме всего прочего, четкой тенденцией к созданию оптимальных по своим качествам конструкций, привело к постановке ряда частных задач, которые были вариационными по существу дела, однако либо не укладывались в привычные рамки вариационного исчисления, либо это удавалось сделать ценой нежелательных искажений задачи. Постепенно выработались некоторые типичные формы новых вариационных задач, получившие имена пионеров этой области так появились задачи Больца, Майера и другие. Отдавая должное этим ученым, мы не будем в дальнейшем пользоваться соответствующей терминологией, так как она отражает лишь историю становления современного вариационного исчисления, но не существо дела. Эти различные по наименованиям задачи не нуждаются ни в специфических методах теоретического исследования, ни в особых подходах при разработке алгоритмов их приближенного решения. Все эти задачи естественно укладываются в сложившуюся в настоящее время форму задачи оптимального управления, теоретический анализ которой не проще и не сложнее анализа упомянутых ее частных видов. Это же отно- [c.23]
Метод локальных вар наций и релаксационный метод. В [86 ] метод локальных вариаций был распространен на задачи минимизации функционалов от функций нескольких независимых переменных. Хорошо известно, что многие задачи математической физики (краевые задачи для уравнения Лапласа, для бигармонического уравнения и другие) могут быть сформулированы либо как задачи на минимум соответствующего функционала, либо как задачи с уравнениями в частных производных (эти уравнения — суть уравнения Эйлера для вариационной формулировки). Применительно к таким задачам метод локальных вариаций состоит из двух элементов. [c.134]
Уикстид рассматривал условия постоянной физической отдачи в качестве универсальных условий.9 Однако он запутался, потому что общественный продукт промышленности с точки зрения удовлетворения явно не растет в той же пропорции, что и используемые в отрасли факторы производства, в то время как коммерческий продукт фирмы увеличивается пропорционально росту используемых ею факторов. Он предложил оригинальный метод для преодоления первого затруднения. В качестве фактора, необходимого для производства удовлетворения ,10 можно также рассматривать и потребителя. Далее, если каждый фактор промышленности, включая и потребителей, увеличить в определенной пропорции, то производимое удовлетворение возрастет в той же пропорции тем самым будут выполнены условия теоремы Эйлера. Но даже с помощью этого приема невозможно преодолеть второе затруднение, и Уикстид понял, что условия постоянной [c.62]
Теоретической основой применения графических методов и моделей, по мнению В.М.Цимбалова1, является прежде всего теория графов, которая зародилась в XVIII в. как математическая задача Эйлера о прогулке по замкнутому маршруту в прусском городе Кенигсберге и была развита в XIX в. в связи с возникшей в Англии математической задачей о четырех красках, решенной лишь совсем недавно. В XX в. теория графов прошла определенные стадии формирования и была признана самостоятельной дисциплиной. [c.59]
Регуляризация функционалов в неограниченных областях. Течения в неограниченных областях, как правило, имеют расходящийся функционал энергии. Для придания смысла вариационным принципам требуется видоизменить (регуляризовать) функционал энергии, не нарушив при этом уравнений Эйлера. Опишем на плоских задачах метод регуляризации, предложенный Шифманом [390]. [c.236]
Из формулы (6.9) видно значение ограничения (6.7) - оно аннулирует ядро квадратичной части функционала J. На множестве функций р, удовлетворяющих условию (6.7), функционал (6.9) является строго выпуклым и имеет единственный минимизирующий элемент. Таким образом, следующий член разложения единственным образом определяется по предьщущему, и множество Ж в общей схеме вариационно-асимптотического метода совпадает с J 0. Функция у находится из уравнений Эйлера [c.355]
