Корреляционный интеграл. Вероятность того, что две точки находятся в пределах определенного расстояния одна от другой. Используется в расчете корреляционной размерности. [c.287]
Вычисление корреляционно размерности [c.276]
Идея различения "хаотических" и "стохастических" последовательностей в работах [448] и [305] основана на том наблюдении, что корреляционная размерность у таких последовательностей различна. Как будет видно из дальнейшего, у "стохастических" последовательностей она больше, чем у "хаотических" [c.225]
Согласно [305] и [448], в качестве оценок корреляционной размерности vm естественно взять величины [c.225]
Из сопоставления этих таблиц видно, что в случае m = 1 весьма трудно по значениям корреляционной размерности v j отличить "хаотичность" и "стохастичность" Привлечение же больших значений m показывает существенное различие в величинах vm
Из сопоставления этих двух таблиц видна, во-первых, однородность "фрактальной" структуры "корреляционной размерности" индексов IBM [c.226]
Корреляционная размерность 225 Коэффициент вытянутости [c.520]
С развитием применения методов современного факторного анализа связана также возможность эффективного решения следующих трех обобщенных статистических задач экономического анализа изучение внутренней структуры связей в системе показателей, изучение размерности описания экономического явления, выявление более информативных показателей. Хотя эти задачи можно решить методами корреляционного и регрессионного анализа, однако при экономическом анализе их следует решать на основе методов современного факторного анализа. [c.115]
Корреляционный интеграл - вероятность того, что любые две точки находятся на определенном расстоянии е друг от друга в фазовом пространстве. По мере того как мы увеличиваем е, вероятность изменяется согласно фрактальной размерности фазового пространства. Корреляционные интегралы рассчитываются согласно следующему уравнению [c.235]
Ст = корреляционный интеграл для размерности m [c.236]
Это типичная особенность масштабирования вероятностных процессов. Корреляционный интеграл просто заполняет пространство любой размерности, в [c.236]
Мы подсчитываем количество пар точек следующим образом. Во-первых, восстанавливаем наш временной ряд как фазовое пространство, начиная с нижней размерности вложения т = 2, как это было показано в предыдущем разделе. Затем, начиная с малого расстояния Л, подсчитываем для него корреляционный интеграл m(R) в соответствии со следующим соотношением [c.183]
На рис. 13.5-13.8 показаны диаграммы корреляционных интегралов для четырех рынков. Линейные области на каждой диаграмме могут быть использованы для построения регрессий. На рис. 13.9-13.12 показана сходимость к фрактальной размерности. В табл. 13.1 дана сводка результатов. [c.198]
Функция Z рассчитывает, сколько точек находится на расстоянии е друг друга. Согласно теории, Ст должно увеличиваться со скоростью е°, где D - корреляционная размерность фазового пространства, которая близко связана с фрактальной размерностью. Вычисление корреляции требует от нас знания того, как выглядит фазовое пространство. В реальной жизни мы не только не знаем факторы, задействованные в системе, мы даже не знаем, сколько их Обычно у нас есть только одна наблюдаемая величина, например, изменения курса акций. К счастью, в теореме Такенса (Takens, 1981) говорится, что мы можем воссоздать фазовое пространство, задерживая один временной ряд, который мы имеем, для каждой размерности, которая, как мы думаем, существует. Если число "размерностей вложения" больше, чем фрактальная размерность, корреляционная размерность стабилизируется к одному значению. В моей предыдущей книге намечены процедуры выполнения этого вычисления на основании экспериментальных данных, взятых из работы Волфа и др. (Wolf et al., 1985). [c.236]
Далее если найдена аномальная величина Я, закономерен вопрос, обоснована ли ее оценка. Можно усомниться в том, достаточно ли было данных, или даже — работает ли вообще Д/5-анализ. Я предлагаю следующий простой тест, основанный в свою очередь на тесте, разработанном Шейнкманом и Ле Бароном (S heinkman, Le Baron, 1989) для корреляционной размерности (которую мы рассмотрим в гл. 12). [c.100]
Для размерности т мы можем вычислять Ст при увеличении Л. Находя наклон прямой на графике линейной регрессии в двойных логарифмических координатах log( m), log(.R), мЬ1 можем оценить корреляционную размерность D для размерности вложения т. При увеличении ш, размерность D будет в конце концов сходиться к своей истинной величине. По причинам, установленным выше, тот же результат имеет место, если размерность вложения становится больше, чем фрактальная размерность. Обычно сходимость наблюдается, когда размерность вложения на три или более целых чисел выше фрактальной размерности. Фрактал, вложенный в более высокую размерность, сохраняет свою истинную размерность по причине корреляций между точками. Таким образом, корреляционная размерность Грассбергера и Прокаччи является хорошей оценкой для фрактальной размерности. Эти две размерности, как показали названные авторы, прямо соотносятся друг с другом. [c.184]
Файл ORRDIM.TXT должен быть переведен в электронную таблицу. Двойная логарифмическая кривая выходного файла даст график, подобный графику рис. 12.2 для аттрактора Хенона. Линейная регрессия применяется к линейному участку этой двойной логарифмической кривой. Ее наклон есть оценка корреляционной размерности. Для аттрактора Хенона размерность вложения известна, поэтому требуется только один ряд в этой размерности. Однако для экспериментальных данных, подобных рыночному временному ряду, размерность вложения нам не известна. Следовательно, мы должны запускать программу неоднократно, увеличивая величины DIMEN до тех пор, пока регрессия не сойдется к единственной величине, как это описано в гл. 13. Эта конвергенция должна произойти до того, как размерность станет слишком большой. В противном случае можно заключить, что данные слишком разрежены для того, чтобы в линейной области подходила двойная логарифмическая кривая. Если налицо такой случай, значит требуется больше данных для оценки размерности, как об этом было сказано в гл. 12 и 13. [c.277]
Корреляционная размерность ( orrelation dimension). Оценка фрактальной размерности, которая (1) является мерой вероятности того, что две случайным образом выбранные точки находятся на определенном расстоянии друг от друга, и (2) показывает, как эта вероятность изменяется с ростом расстояния. Зависимые системы будут удерживаться вместе своими корреляциями и сохранять свою размерность независимо от того, в пространство какой размерности они помещены, пока размерность пространства больше их фрактальной размерности. Белый шум будет заполнять свое пространство, поскольку его компоненты не коррелированны и его корреляционная размерность равна размерности любого пространства, в которое он помещается. [c.307]
Корреляционный интеграл ( orrelation integral). Вероятность того, что две точки находятся на определенном расстоянии друг от друга, определяется суммой или интегралом по ячейкам фиксированного размера в пространстве состояний используется при расчете корреляционной размерности. [c.307]
Фрактальный анализ рынка (Fra tal market analysis). Метод измерения памяти временного ряда, фрактальной размерности и/или корреляционной размерности временного ряда. См. также Анализ нормированного размаха, Фрактальная размерность, Корреляционная размерность. [c.315]
| Рис. 81. Степень фрактальной размерности троичного канторова множества, измеренная корреляционным методом. Рисунок изображает логарифм корреляционного интеграла как функцию логарифма размерности. Источник [387]. | ![Рис. 81. Степень <a href="/info/146124">фрактальной размерности</a> троичного канторова множества, измеренная корреляционным методом. Рисунок изображает логарифм корреляционного интеграла как функцию логарифма размерности. Источник [387].](/pic1/081032129097005197001193083182054186029231127126.png) |
Корреляционный интеграл из уравнения (16.2) вычисляет вероятность того, что две точки, которые являются частью двух различных траекторий в фазовом пространстве, отстоят друг от друга на е единиц. Предположим, что Xj во временном ряде X (с наблюдениями Т) независимы. Мы задерживаем этот ряд в "историях N" то есть мы используем метод задержки времени Такенса для создания фазового пространства размерности N из временного ряда X. Затем мы вычисляем корреляционный интеграл См(е,Т), используя уравнение (16.2). Брок и др. показали, что по мере приближения Т к бесконечности [c.236]
| Рис. 12.2. Корреляционный интеграл аттрактор Хенона оценк фрактальной размерности 1.25. | 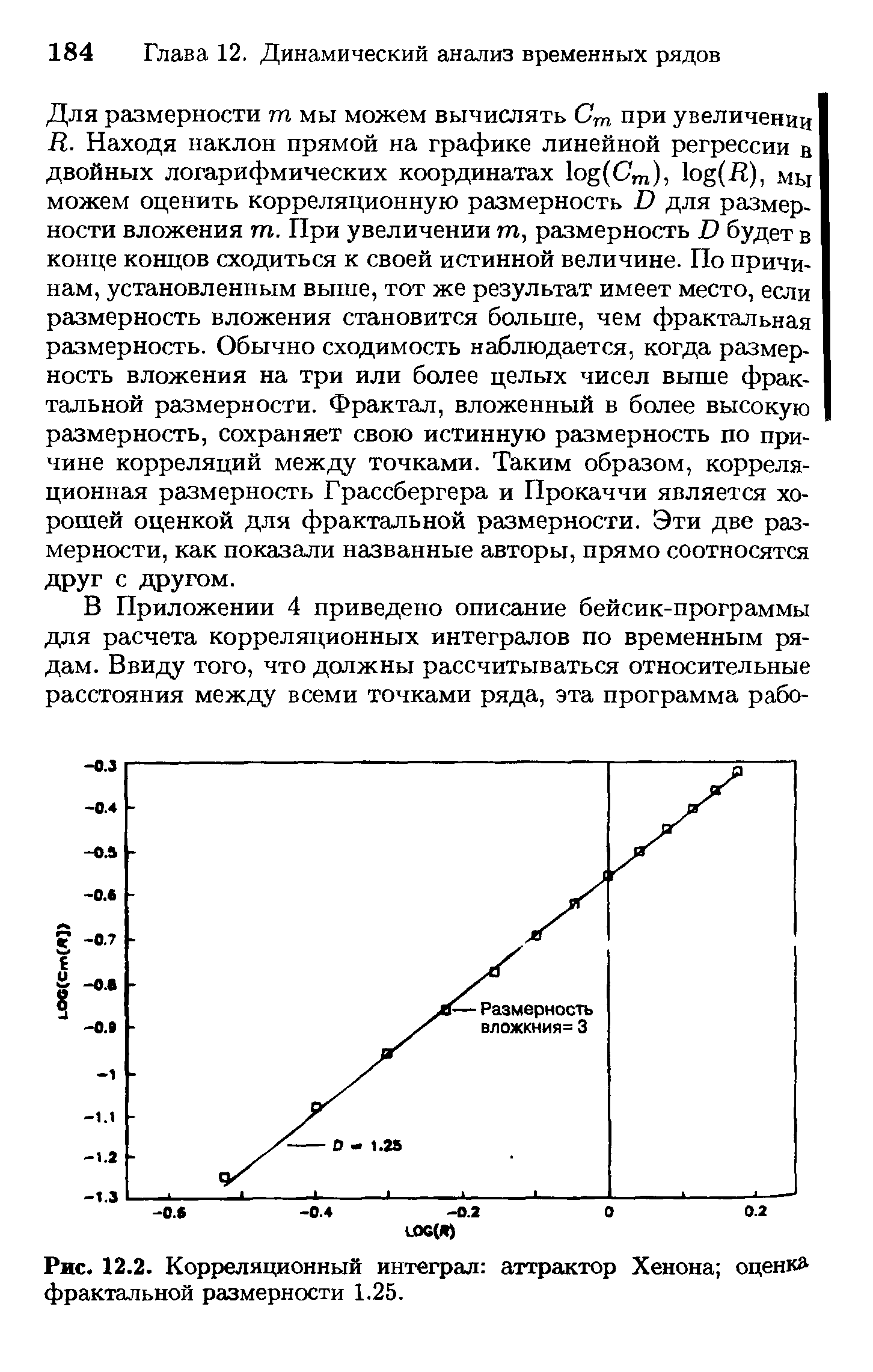 |
Выходной файл ORRDIM.TXT напечатает расстояние (R) и корреляционный интеграл ( R) в колонке для этой размерности вложения. Нажмите кнопку View для изучения выходных данных. [c.277]
Если известна корреляционная матрица невырожденного нормального вектора с ДСЗ, то по ней с помощью известного в теории графов алгоритма Крускала граф структуры зависимостей восстанавливается однозначно. Алгоритм Крускала, примененный к выборочной корреляционной матрице, оказывается состоятельным в асимптотике Колмогорова -г- Деева, специально рассчитанной на изучение ситуаций, когда число наблюдений вектора и его размерность суть величины одного порядка. [c.162]
В предобработке можно условно выделить несколько видов. В первую группу можно условно отнести восстановление пропущенных данных, редактирование аномальных значений, вычитание шума, сглаживание. Для этих целей используются такие алгоритмы, как корреляционный, факторный, регрессионный анализ. В другой группе осуществляется понижение размерности входных данных и устранение незначащих факторов. Используются алгоритмы робастной фильтрации, спектрального и вейвлет анализа, последовательной рекуррентной фильтрации, статистического анализа. На практике предобработка исходных данных может осуществляться в произвольной последовательности с произвольными параметрами на каждом шаге любое число раз, то есть сценарий предобработки может быть довольно сложным. [c.40]
Смотреть страницы где упоминается термин Корреляционная размерность
: [c.150] [c.235] [c.237] [c.267] [c.287] [c.183] [c.211] [c.277] [c.225] [c.226] [c.482] [c.312] [c.116] [c.183] [c.185] [c.197]Основы стохастической финансовой математики Т.2 (1998) -- [ c.225 ]
