Здесь г радиус-вектор точки пространства, г0 — радиус-вектор центра сферы. При больших q/a гармоническая функция [c.245]
Эвристическая теория оболочек. Меры деформации. Деформированное положение оболочки естественно моделировать поверхностью в трехмерном пространстве обозначим ее через Л. Закон движения поверхности Г2 задается функциями х = г (%а, г), где r (%a, f) — компоненты радиус-вектора точки поверхности с лагранжевыми координатами °v В начальном состоянии поверхность J2 занимает положение П, задаваемое уравнениями х = г (%а) = г ( а, Г0). [c.261]
Вектор ОМ, где 0(0, 0,. . ., 0), называют радиусом-вектором точки М. [c.75]
Радиус-вектор точки 75 Радиус сходимости 176 Разложение вектора 45 — определителя 63 [c.329]
| Рис. 1. Угол наклона к оси абсцисс кривой в точке М — это угол наклона касательной MN он характеризует предельную величину / ( ) Угол наклона радиуса—вектора ОМ характеризует среднюю величину /( ) | 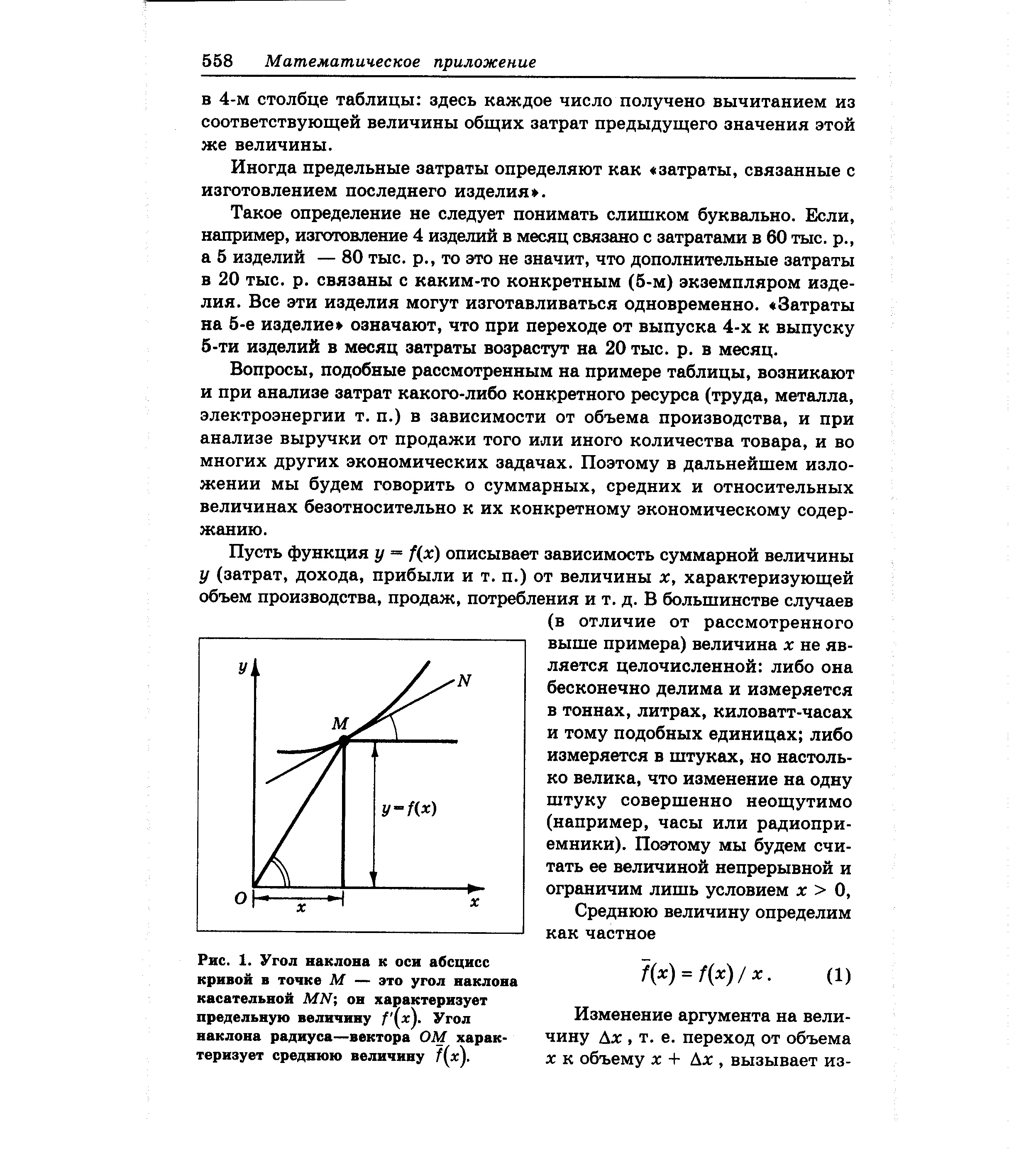 |
Если f(x) = ах, то /(х) = а и /"(х) = а, т. е. в случае, когда суммарная величина пропорциональна аргументу, средняя величина совпадает с предельной при всех значениях х. Графиком такой зависимости служит прямая, проходящая через начало координат, Радиус-вектор любой точки на этой прямой целиком лежит на ней касательная к прямой — сама эта прямая, так что в рассматриваемом случае оба угловых коэффициента совпадают. [c.559]
На рис. 2 есть такая точка — L. Здесь радиус-вектор касается графика функции, или, что то же самое, касательная проходит через начало координат. [c.561]
Случай а. Если вокруг точки х4 образовать сферическую поверхность радиусом /3, то пересечение траекторий, образованных Ri и Pi, получится в точке х2 (фиг. 1 и 2). Поскольку вектор (OO Pi/Vs) должен находиться в идентичной плоскости, а вектор х4 должен лежать в плоскости, которая определяется углом вращения / ь т. е. 0ь то GI можно получить из х4- Оче- [c.308]
Максимальное число решений для случаев а — г не учитывает особых решений. На фиг. 2 показана точка пересечения х2 для случаев а — г . Радиус-вектор Р Р2 в случае а определяется путем экстраполяции, а для случаев б — г — последовательными вычислениями. [c.309]
Прежде всего необходимо определить радиус-векторы хь х2 для Р, PZ (фиг. 1). Поскольку 2 является радиус-вектором для Р2 на том же рисунке, то для случаев а — в х2 выражается через GI и 62 [c.310]
Таким путем находятся х, = х2, х4, х6 и радиус-векторы пространства всех точек вращения. [c.312]
Так, например, если расстояние от торгового центра А до торгового центра В по главной транспортной магистрали составляет 8 км, число жителей населенного пункта А равно 38 000 чел., а число жителей населенного пункта В — 62 000 чел., то радиус-вектор ЗПСПУ торгового центра А равен [c.131]
Другой дополняющий метод состоит в том, чтобы сделать выборку покупателей, посещающих центр торговли, и узнать места их жительства. Результаты опроса затем переносятся на крупномасштабную карту местности, и место каждого опрошенного покупателя помечается на ней точкой. Еще одно полезное дополнение метода — это обозначение каждой покупательской группы разным цветом. Такая карта показывает сосредоточение отдельных групп покупателей. Это очень удобно, например, для целенаправленной рекламы, а также определения величины радиус-векторов, определяющих размеры ЗПСПУ каждого из торговых центров в пределах одного населенного пункта. [c.133]
Полученные значения радиус-векторов t. откладываем от нулевой оси, соединяющей гг. Ульяновск и Челябинск, причем нулевая точка расположена в г. Челябинске. Соединяя между собой полученные точки, строим линию разграничения 1 ЗПСПУ предприятий Аи В. [c.226]
Если < /> = 0, то г имеют смысл компонент среднего радиус-вектора поперечного волокна в деформированном. состоянии с весом г = (fxl >, а у — среднего поворота в весом / А = < f/x ) / < f 2/>. [c.307]
Всякое комплексное число z = a+bi удобно изображать точкой (a, b) или соответствующим радиусом-вектором на комплексной плоскости (рис. 1.23). Оси Ох и Оу прямоугольной декартовой системы координат называют при этом соответственно Действительной и мнимой осью. Величину р—длину рад,иуса-вектора точки г называют [c.31]
Пусть г > 0 — радиус шара В (с) и пусть и — точка в Rn, такая что и < г, при этом с + и G В (с). Выражая вектор и через его компоненты, получаем [c.128]
Если для инициализации модельных векторов используются случайные числа, то приведенные выше рекомендации относительно выбора значений N (t) и а( ), не годятся. В этом случае начальный радиус N должен составлять половину размера сети, и скорость обучения должна быть близкой к единице в начале процесса. Хотя этот вариант был неоднократно подтвержден экспериментально, применять инициализацию случайными числами на практике мы не рекомендуем Лучше остановиться на регулярных начальных значениях, поскольку нет необходимости всякий раз демонстрировать действие алгоритма самоорганизации в полном объеме. [c.267]
Рис. 1. иллюстрирует геометрические свойства введенных величин. Возьмем на графике функции суммарной величины произвольную точку М. Ее координаты х и у = f(x). Проведем отрезок из начала координат в точку М (он называется радиусом-вектором точки М). На рисунке видно, что угловой коэффициент радиуса-вектора представляет среднюю величину /(х). Предельной величине соответствует угловой коэффициент касательной к графику в точке М. [c.559]
Немалый интерес представляет собой анализ влияния расстояния до государственной фаницы tBW на конфигурацию линии разфаничения ЗПСПУ. При определенном соотношении pw/pv наблюдается нарушение целостности ЗПСПУ одного из предприятий. Так, например, при отсутствии таможенного тарифа и увеличении параметра/ до величины 4,3 д-e.W/KM данная зона состоит из трех локальных частей I, II, III, представленных на рис. 3.23. Очевидно то, что чем больше расстояние транспортировки продукции до государственной фаницы, тем меньше величина радиус-вектора ЗПСПУ. То же самое можно сказать и в отно- [c.128]
Вначале все города оказывают приблизительно одинаковое влияние на каждую точку маршрута. В последующем, большие расстояния становятся менее влиятельными и каждый город становится более специфичным для ближайших к нему точек кольца. Такое постепенное увеличение специфичности, которое, конечно, напоминает уже знакомый нам метод обучения сети Кохонена, контролируется значением некоторого эффективного радиуса R. Если обозначить через X,. вектор, определяющий положение / -го города на плоскости, a Yy - [c.115]
