ИНДЕКС ГАРМОНИЧЕСКИЙ — относительный показатель изменения сложного экономич. явления, вычисляемый в форме средней гармонической взвешенной из относительных показателей изменения отдельных элементов этого явления (из т. н. индивидуальных индексов). [c.265]
Индексным методом можно выявить влияние на изучаемый совокупный показатель различных факторов. Статистика называет несколько форм индексов, которые используются в аналитической работе (агрегатная, арифметическая, гармоническая и др.). [c.52]
Здесь следует напомнить, что агрегатный индекс является основной формой всякого общего индекса его можно преобразовать как в средний арифметический, так и в средний гармонический индексы. [c.53]
Такой пересчет товарооборота в сопоставимые цены по схеме агрегатного индекса может быть проведен, если товары (сырье, готовая продукция) учитываются не только по сумме, но и по количеству. Если количественный учет не ведется, то индекс физического объема определяется отношением индекса оборота в действующих ценах и индекса цен, исчисленного по схеме среднего гармонического индекса [c.54]
Приведенный пример наглядно иллюстрирует преобразование агрегатного индекса в средний гармонический. [c.54]
Общие индексы цен строят различными способами в зависимости от поставленной задачи и наличия исходных данных. Наиболее часто используются агрегатная, арифметическая, гармоническая и реже — геометрическая формы индексов цен. [c.554]
II. Агрегатные, средние арифметические и средние гармонические взвешенные индексы цен Индекс [c.557]
Предложен немецким экономистом Германом Пааше (1874). Представляет собой сравнение агрегированных цен, взвешенных по физическим объемам текущего периода, или гармоническую среднюю индексов цен, взвешенных по стоимости текущего периода [c.557]
ППС между валютами двух стран рассчитываются, используя те же виды индексов, что и при динамическом сопоставлении цен. На уровне первичных товарных групп используется формула среднего гармонического невзвешенного индекса из индивидуальных соотношений цен [c.724]
Используя в качестве весов затраты на покупку в отчетном периоде, получаем сводный индекс цен как средний гармонический взвешенный из индивидуальных индексов цен [c.376]
В зависимости от формы построения различаются индексы агрегатные и средние. Последние делятся на арифметические и гармонические. Агрегатная форма общих индексов является основной формой экономических индексов. Средние индексы — производные, они получаются в результате преобразования агрегатных индексов. [c.93]
Средний индекс — это индекс, вычисленный как средняя величина из индивидуальных индексов. Он должен быть тождествен агрегатному индексу. При исчислении средних индексов используются две формы средних арифметическая и гармоническая. Среднеарифметический индекс тождествен агрегатному, если весами индивидуальных индексов будут слагаемые знаменателя агрегатного индекса. Только в этом случае величина индекса, рассчитанного по формуле средней арифметической, будет равна агрегатному индексу. [c.99]
| Таблица 16.1. Агрегатные, арифметические и гармонические формы индексов цен | 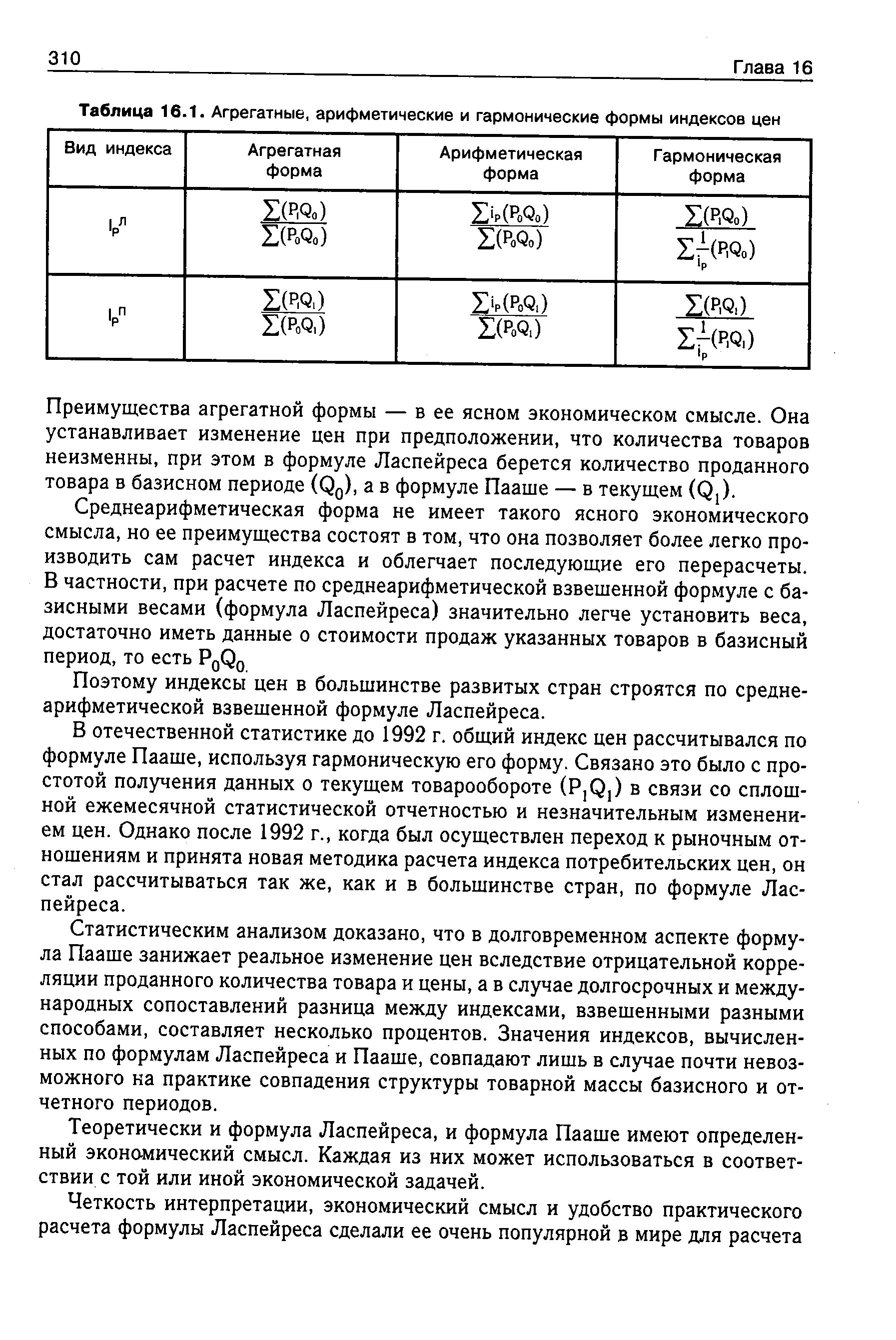 |
В отечественной статистике до 1992 г. общий индекс цен рассчитывался по формуле Пааше, используя гармоническую его форму. Связано это было с простотой получения данных о текущем товарообороте (P,Qj) в связи со сплошной ежемесячной статистической отчетностью и незначительным изменением цен. Однако после 1992 г., когда был осуществлен переход к рыночным отношениям и принята новая методика расчета индекса потребительских цен, он стал рассчитываться так же, как и в большинстве стран, по формуле Ласпейреса. [c.310]
В то же самое время государственные органы статистики исчислили индекс цен за февраль по формуле простой гармонической средней [c.191]
Абсолютные величины характеризуют абсолютные значения показателей, относительные — соотношение различных абсолютных показателей (темпы роста в процентах, удельный вес, коэффициенты, индексы). Средние величины выражают типичные свойства изучаемой совокупности качественно-однородных, но количественно не совпадающих друг с другом явлений (средняя заработная плата рабочих, средняя загрузка оборудования, средняя выработка). Наиболее распространенные виды средних — средняя арифметическая (простая и взвешенная) и средняя геометрическая. При отсутствии прямых данных о весах применяется средняя гармоническая. Используются также среднее линейное и среднее квадратичное отклонения, коэффициент вариации. [c.251]
Индекс цен — это обобщающий показатель изменения уровня цен. Он отражает изменение общего уровня цен определенной совокупности товаров. Распространенными типами индексов цен являются агрегатный и средний гармонический. Большинство индексов цен исчисляется по агрегатной формуле с весами текущего периода - [c.300]
Агрегатный индекс цен исчисляется во всех случаях, когда имеются отчетные данные о количестве реализованной (произведенной) продукции в натуральном выражении. Если же учет продукции ведется только в стоимостной форме, то расчет индекса цен осуществляется по формуле среднего гармонического индекса [c.300]
Индексы государственных розничных цен исчисляются по формуле среднего гармонического индекса. Весами индексов являются массовые данные статистики торговли об общем объеме и структуре розничного товарооборота в стоимостном выражении за отчетный период. Индексы цен определяются путем оценки стоимости товаров, проданных в отчетном периоде, в ценах отчетного и базисного периодов. Переоценка объема товарооборота, учитываемого в текущих ценах, в цены базисного периода производится по отдельным группам на основании специально исчисляемых групповых индексов цен. В практике расчетов таких групповых индексов цен применяются различные методы и схемы расчетов в зависимости от особенностей ценообразования и реализации товаров, входящих в ту или иную товарную группу. [c.309]
Получение групповых и общих индексов возможно при помощи той или другой формы средней. В зависимости от выбранной формы средней индексы могут быть арифметическими, гармоническими, геометрическими и агрегатными. Агрегатная форма индексов является основной и заключается она в следующем берётся отношение двух агрегатов, один из которых относится к базисному периоду, а другой — к текущему (отчётному). Исчисляется агрегатный индекс цен по формуле [c.430]
Арифметический, гармонический и геометрический индексы получаются как средние из индивидуальных, а агрегатный индекс получается в результате соотношения сумм агрегатов текущего и базисного периодов. [c.430]
Средней гармонической называется обратная величина средней арифметической из обратных величин. Напр., индивидуальный индекс цены обычно обозначается как —-, а обратная ему величина как 1 —- = [c.265]
В сов. индексной практике принято считать главной ( основной ) формой И. ц. агрегатный с весами д, текущего периода, а поэтому из числа средних индексов считают пригодными лишь арифметические с условными весами р и гармонические с весами p i, при к-рых оба эти индекса тождественно совпадают с агрегатным И. ц. Число товаров, включаемых в набор для И. ц., неизбежно ограничено по сравнению со всей массой видов обращающихся товаров, поэтому для И. ц. отбирают относительно немного товаров-представителей целых групп родственных товаров с приблизительно однородным, иногда даже одинаковым характером динамики цен. Однако существуют И. ц. с наборами в несколько сотен и даже тысяч товаров (например, И. ц. оптовых Министерства торговли Великобритании, ок. 7 тыс. товаров). Любой И. ц. способен отразить динамику лишь частного уровня тех цен, к-рые положены в его основание, напр. уровня оптовых цен, уровня розничных цен, цен в гос. или в кооперативной торговле, цен колхозного рынка, заготовительных и т. п. задача сведения всех этих частных И. ц. в единый индекс общего, тотального уровня всех цен страны пока практически не ставилась и в статистич. теории но обсуждалась. Частный важный случай И. ц. — индекс себестоимости к И. ц. в расширенном понимании можно отнести н И. ц. потребительских услуг (в непроизводств. сфере нар. х-ва). Под И. ц. обычно понимают индексы дина м и к и их уровня, его изменения во в р е-м е н и. Однако немаловажное экономич. значение имеют территориальные И. ц., теоретически ещё мало разработанные и практически пока редко вычисляемые. Их назначение — количественно выражать соотношение одновременно сосуществующих уровней однотипных цеп в пространстве, напр. уровней розничных цен в гос. торговле в Московской и в Одесской областях (с разными поясами цен п различной структурой потребления), уровней цен на колхозных рынках в городах и в сельских местностях, уровней фактич. закупочных цен в разных союзных республиках и т. п. Способы построения таких И. ц. могут быть аналогичны общим способам исчисления индексов территориальных за стандартизованные базисные цены и веса могут быть приняты средние цены и натуральные величины потребления отдельных товаров во всём СССР. Величина, обратная 1 [c.559]
Индекс Пааше (средняя гармоническая формула) [c.221]
Итак, мы рассмотрели четыре способа выявления сезонной компоненты аддитивную модель, мультипликативную модель, метод экспоненциального сглаживания с тремя параметрами, гармонический анализ Фурье (рис. П-7). В нашем примере оказалось, что наименьшую ошибку дает мультипликативная модель, т. е. применение индексов сезонности. [c.439]
При выводе (9.17) учтено, что интеграл по Кот Д обращается в нуль, так как <р — гармоническая функция. Индекс (е) подчеркивает, что в интеграле (9.17) берутся предельные значения величин при подходе к ЪА со стороны жидкости. [c.247]
Тот же индекс может быть записан в форме средней гармонической величины [c.117]
В форме средней гармонической индекс физического объема практически никогда не используется. [c.117]
Формула индекса цен Пааше может быть представлена как взвешенное среднее гармоническое индивидуальных индексов цен с весами, равными долям стоимости представителей в корзине текущего периода [c.115]
Таким образом, сводные индексы цен Ласпейреса и Пааше могут быть представлены и как отношения стоимостей корзин товаров-представителей в сопоставляемые периоды, и как взвешенные средние (арифметические или гармонические) индивидуальных индексов цен. Соответственно их можно интерпретировать и как изменение стоимости корзины, и как меру расположения распределения индивидуальных индексов. Аналогично — индексы количеств. [c.115]
И в этом случае проблема состоит в том, что получить меру расположения совокупности индивидуальных индексов можно многими способами. Для этого можно использовать разные виды средних (арифметическое, геометрическое, гармоническое и т. д., см. [60]) и разные системы весов. Поэтому и при использовании этого подхода разные индексные формулы дают, вообще говоря, разные результаты сопоставлений. [c.115]
Сводный индекс цен можно представить как некоторое среднее индивидуальных индексов (например, взвешенное среднее арифметическое, гармоническое, геометрическое). Смещение, обусловленное замещением на верхнем уровне построения индекса цен, может возникать тогда, когда на шаге по времени сцепленного индекса используются устаревшие веса, т.е. когда весовая база не соответствует середине шага по времени. При этом разные способы осреднения, лежащие в основе используемых индексных формул, могут приводить к различным по величине, и даже по направлению, смещениям, обусловленным замещением. [c.49]
Индексный метод основывается на сопоставлении показателей отчетного и базисного периодов. Основным условием при этом является то, что сопоставляемые величины должны быть идентичны, т. е. рассчитываться одинаково (в одной методологии) или в одних ценах (в ценах базисного или отчетного периода) и обязательно в одних единицах измерения. Индексный метод — один из наиболее распространенных, поскольку с его помощью можно выявить влияние на изучаемый совокупный показатель различных факторов. В практике статистических и аналитических расчетов известно несколько форм индексов агрегатная, арифметическая, гармоническая и др. [c.44]
Агрегатный индекс является основной формой всякого общего индекса. Именно агрегатный индекс можно преобразовать в средний арифметический или средний гармонический индекс. Схема расчета агрегатного индекса следующая [c.44]
Применительно к изменению физического объема продаж, если товары учитываются не только по ценам (Ц), но и по количеству (N), индекс рассчитывается так IN = 2N Ц/ SN U,. Если количественный учет не ведется, то индекс физического оборота определяется отношением индекса оборота в действующих ценах и индекса цен, исчисляемый по схеме среднего гармонического индекса 1Ц= ш. Ц7/ Ш7 Ц = N7 nV (1/1ц №Ц), где 1Ц = Ц /Ц [c.14]
Применение И. м. в с. позволяет решать задачи синтетического и аналитич. порядка, т. к. индексы выражают, с одной стороны, соотношения величин сложных экономич. явлений (сннтетич. значение), а с другой стороны — изменения общих итоговых показателей под действием определенных факторов. Напр., индекс цен выражает влияние изменения цен на изменение общей стоимости продукции (аналитич. значение). Применяя II. м. в с., следует различать содержание индекса и его форму. По содержанию различаются конкретные индексы объема продукции, себестоимости, цен, трудоемкости, производительности труда, объема работ и т. д. Цель исследования и характер изучаемого явления определяют содержание индекса. По форме вычислений различаются индекс агрегатный, индекс арифметический и индекс гармонический. f [c.267]
В экономической литературе считается, что первый индекс цен был построен итальянским экономистом Карли в 1 764 г. Этот индекс был построен по среднеарифметической формуле без применения какой-либо системы взвешивания. В XIX веке при построении индексов цен, в основном по агрегатной или соответствующей ей среднеарифметической формуле, статистики начинают использовать систему взвешивания. В зависимости от выбора базисных или текущих весов возникли две формулы Ласпейреса (1871 г.) и Пааше (1874 г.). Более широкое практическое применение находят две другие их формы в формуле Ласпейреса — средняя арифметическая форма, в формуле Пааше — средняя гармоническая, которые отражены в табл. 16.1. [c.309]
Когда выше говорилось о зодиакальных положениях планет, то подразумевалось, что речь идет о геоцентрических положениях. Однако Роберт Хэнд предложил использовать при вычислениях индексов гелиоцентрические положения планет. Это предложение основано на том, что гелиоастрология более тесно связана с глобальными событиями на Земле, чем геоцентрическая астрология (в которой положения планет на зодиакальном круге даже зависят от места нахождения земного наблюдателя, это различие для Луны может достигать одного градуса). Р.Хэнд разработал компьютерную программу, которая вычисляла гелиоцентрический индекс, причем не только для гелиоцентрической карты, но и для любой ее гармоники (гармонической карты любого порядка). Есть основания полагать, что некоторые гармоники даже более тесно связаны с финансовой сферой, чем радикс (например, четвертая, а также, возможно, вторая и восьмая гармоники). [c.60]
Индексы закупочных цен исчисляют по формуле среднего гармонического индекса исходя из объема и структуры закупок отчетного года и средних закупочных цен отчетного и предыдущего годой. Средние цены, используемые в расчетах индексов, включают надбавки за увеличение продажи сельскохозяйственных продуктов. Вместе с тем исключаются сортовые надбавки, а также скидки за качество продукции, что позволяет избежать влияния на индекс цен изменений в качестве продукции. По отдельным группам в целях элиминирования влияния на индекс цен ассорти- [c.308]
ИНДЕКСЫ в статистике (от лат. index — указатель, показатель), относительные величины, количественно характеризующие сводную динамику (реже — изменение в пространстве) разносоставной совокупности. Так, / сссР°Т4/5о"= ° 76 (или 76%) озца-чает, что общий уровень всех розничных цен в гос. торговле СССР в 1964 но сравнению с уровнем их в 1950 был 0,70, или 70% (иначе говоря взятые в совокупности, эти цены понизились с 1950 по 1904 в среднем на 0,24, или на 24%). Соно-купность является разносоставной по данному признаку, если итоговую величину этого признака во всей совокупности прямым, непосредственным суммированием его значений у отдельных единиц вычислить нельзя (напр., натуральная величина продукции, состоящей из вещественно разных физич. единиц или частей) или если такое суммирование, формально хотя и возможное, приводит к результату, лишённому эко-номпч. смысла (напр., сумма цен вещественно разных товаров, взятых лишь по одной единице натурального измерения). Четырьмя элементами любого И. являются а) индексируемая величина б ) тип (форма) И. в) веса И. г) сроки исчисления. В зависимости от элемента (а) возможны И. цен, И. физич. (натурального) объёма продукции, И. производительности труда н т. д. В зависимости от типа (б) различают И. агрегатные и И. средние, а среди последних, смотря по форме средней, И. средние арифметические, И. средние геометрические, И. средние гармонические и т. д. В зависимости от весов (в) различают И. простые (невзвешенные) п И. взвешенные, а среди последних — И. с постоянными (неизменными) весами и И. с переменными весами ( в меру необходимости с течением времени пересматриваемыми). В зависимости от сроков исчисления (г) рассматривают И. базисные (с постоянной, неизменной во времени базой) и И. цепные (если числовые значения индексируемой величины в каждый данный текущий срок сопоставляются с их значениями в предшествующий срок иначе, И. с переменной базой) в общем случае произведение соответствующих цепных И. [c.551]
Величины а и j3 пробегают счетное число значений, однако, во избежание громоздких обозначений, индексов у а и 0-не ставится. Точно так же подразумевается, что каждому значению а и 0 соответствуют свои значения м, , ф и ма, однако эти значения не нумеруются. Дальше будут введены дополнительные обозначения, которые исключают недоразумения. В каждом частном решении и, фа, ф и иа произвольным образом зависят от продольных координат и гармонически зависят от времени с частотой со. Частота со для каждого частного решения определяется по соответствующим значениям а или 0 из формул [c.314]
