В других формах индексов — индексе арифметическом и индексе гармоническом — взаимосвязь явлений выражается не прямо, а косвенно — в весах т. н. индивидуальных индексов. [c.264]
Базовые стандарты — это нормативы, не корректирующиеся после их первоначального определения, если не происходит существенных изменений в технических характеристиках продукции или в процессе ее производства. Базовые стандарты определяются историческим способом , суть которого заключается в накоплении информации об издержках за определенный промежуток времени и выведении среднего арифметического на единицу продукции или на час работы. Этот метод уже сам по себе переносит неэффективность работы прошлого периода на будущее. Базовые стандарты спустя какое-то время устаревают и поэтому не отражают действующие эффективные методы производства. Следовательно, они не обеспечивают точную информацию о себестоимости продукции, не позволяют эффективно контролировать затраты, но могут быть использованы для исчисления индекса цен. [c.120]
Индексным методом можно выявить влияние на изучаемый совокупный показатель различных факторов. Статистика называет несколько форм индексов, которые используются в аналитической работе (агрегатная, арифметическая, гармоническая и др.). [c.52]
Здесь следует напомнить, что агрегатный индекс является основной формой всякого общего индекса его можно преобразовать как в средний арифметический, так и в средний гармонический индексы. [c.53]
Элементарные статистические методы подразделяют следующим образом 1) статистическое упорядочение — упорядочение информации по определенным принципам 2) абсолютные и относительные показатели 3) расчеты средних величин — среднее арифметическое — простое, взвешенное, среднее геометрическое 4) динамические ряды — абсолютный прирост, относительный прирост, темпы роста, темпы прироста 5) сводка и группировка показателей по отдельным признакам 6) сравнение — с конкурентами, с нормативами, в динамике 7) индексы — влияние факторов на сравниваемые показатели 8) детализация, например годовая производительность определяется производительностью в единицу времени и рабочим временем в году. [c.70]
Общие индексы цен строят различными способами в зависимости от поставленной задачи и наличия исходных данных. Наиболее часто используются агрегатная, арифметическая, гармоническая и реже — геометрическая формы индексов цен. [c.554]
II. Агрегатные, средние арифметические и средние гармонические взвешенные индексы цен Индекс [c.557]
Арифметическая средняя индексов, взвешенных по условной стоимости произведенной продукции текущего периода в базисных ценах [c.558]
Простая арифметическая Сейчас включает 300 акций из 14 Индексы Торонтской средняя, способ взвешенной секторов фондовой биржи [c.768]
Рассмотрим пример. В США с конца XIX в. для группы ведущих акционерных компаний исчисляется так называемый индекс Доу Джонса - арифметическая средняя величина котировок акций на фондовых биржах. Этот показатель характеризует хозяйственную конъюнктуру если индекс Доу Джонса повышается, т.е. растет относительная цена акций, значит, вкладчики капитала рассчитывают получить по акциям больший дивиденд (распределяемая часть прибыли). Это говорит о росте деловой активности. Падение индекса Доу Джонса говорит о снижении деловой активности в стране. Величина этого показателя есть отношение в процентах цени акций на бирже к их номиналу (первоначальной цене при выпуске акций). Это отношение зависит не только от колебаний деловой активности, но имеет также общую тенденцию роста ввиду инфляции - падения покупательной силы доллара США. С начала века этот рост значителен, поэтому в наше время индекс Доу Джонса составляет более 2000% (акция, когда - то выпущенная на сумму 100 долл., теперь стоит более 2000 современных долларов). [c.309]
Если обозначить удельный вес отдельных затрат d0i, то получим общий индекс цен как средний арифметический взвешенный из индивидуальных индексов цен [c.371]
По данным табл. 10.4 простая средняя арифметическая из индивидуальных индексов количества равна [c.378]
Ранее мы рассмотрели вычисление индексов единичных значений во времени. Одна из больших трудностей, связанных с вычислением индексов, возникает тогда, когда проводится сравнение сложных данных. Так, чтобы сравнить стоимость жизни за два года, необходимо учесть цены на многие предметы, например, продукты питания, жилье, одежду, электричество и транспорт. Изменения по каждой из этих позиций повлияют на общую стоимость жизни, и поэтому необходимо каким-то образом свести эти изменения в единый показатель. Рассмотрим расчет индекса цены для нескольких товаров. Два простых метода определения единого индекса, сочетающего все изменения отдельных значений, основаны на применении понятий среднего арифметического и простого агрегата. Теперь в нескольких словах охарактеризуем эти методы. [c.162]
В зависимости от формы построения различаются индексы агрегатные и средние. Последние делятся на арифметические и гармонические. Агрегатная форма общих индексов является основной формой экономических индексов. Средние индексы — производные, они получаются в результате преобразования агрегатных индексов. [c.93]
Средний индекс — это индекс, вычисленный как средняя величина из индивидуальных индексов. Он должен быть тождествен агрегатному индексу. При исчислении средних индексов используются две формы средних арифметическая и гармоническая. Среднеарифметический индекс тождествен агрегатному, если весами индивидуальных индексов будут слагаемые знаменателя агрегатного индекса. Только в этом случае величина индекса, рассчитанного по формуле средней арифметической, будет равна агрегатному индексу. [c.99]
Общий индекс жестких параметров (/п(ж)) рассчитывается как средняя арифметическая из параметрических индексов, взвешенных по рангам важности (/ г (ж)), определяемым экспертным путем [c.260]
Учитывая, что и мягкие параметры товара различаются по степени важности для потребителя, то в целях расчета объективного сводного параметрического индекса каждому частному параметрическому индексу присваивается вес (ранг значимости, определяемый экспертным ранжированием признаков товара по степени их важности - Wi ( м )). Сводный индекс мягких параметров (/ п (м)) также исчисляется как средняя арифметическая взвешенная из частных параметрических индексов [c.260]
ИНДЕКС РЫНОЧНОЙ СИТУАЦИИ - интегральный оценочный показатель состояния рынка, обобщающий характеристику состояния и развития основных параметров рынка исчисляется как средняя арифметическая из балльных оценок параметров и факторов рынка, взвешенных по рангам роли каждого параметра в формировании рыночной ситуации (определяются экспертным путем). [c.306]
| Таблица 16.1. Агрегатные, арифметические и гармонические формы индексов цен | 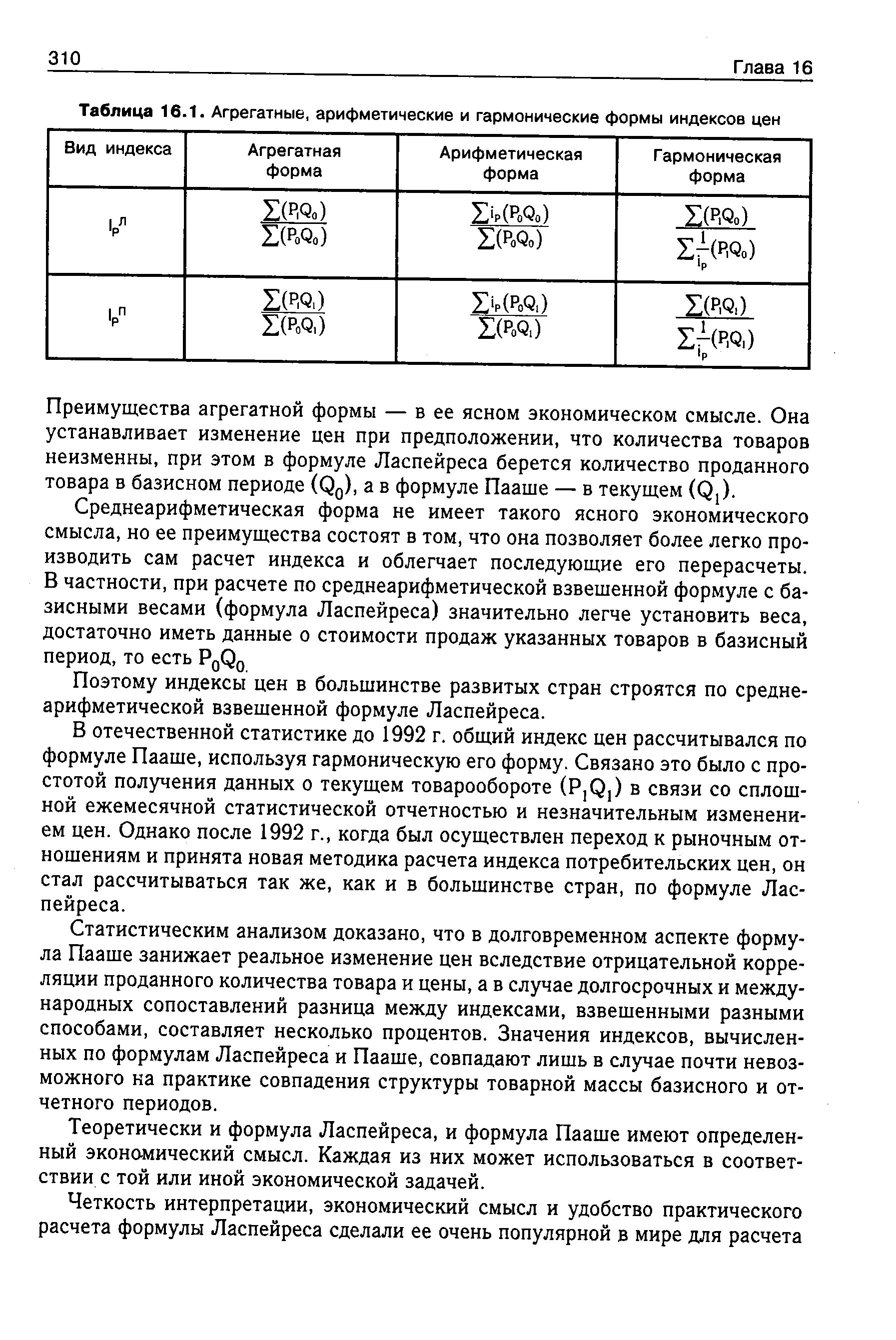 |
Суть этого индекса заключается в расчете простой средней арифметической из цен акций, которые были проданы на бирже. Таким образом, он отражает средний уровень цен. Этот индекс вычисляется по следующей формуле [c.315]
Однако при этом упускается из виду, что средняя арифметическая из цепных индексов всегда больше их средней геометрической. Средний коэффициент роста в данном случае поэтому получается выше действительно го, и сумма членов теоретического ряда оказывается больше соответствующей суммы исходного, т. е. имеем налицо систематическое смещение аналогично предшествующему случаю. [c.129]
Эти данные позволяют продемонстрировать методы, применяемые для расчета интегральных индексов акций. Так, в соответствии с первым подходом, основанном на вычислении темпа роста (снижения) среднеарифметической цены всего множества акций корпораций, этот индекс будет равен 1,1257 ( 60/ 53,3) или 12,57%. Именно по этой методике исчисляли до 1928 г. индексы Доу-Джон-са (до того в промышленный индекс включали цены акций 20 компаний, и знаменатель в формуле среднего арифметического равнялся 20). В настоящее время идея усреднения цены в этих индексах сохранилась, однако знаменатель корректируют на величину дробления акций, дивидендов, выплачиваемых в форме акций и составляющих свыше 10% рыночной стоимости выпусков. Кроме того, учитывают ряд других особенностей (в том числе слияние и поглощение корпораций). [c.18]
Для каждого из 21 товарного рынка, входящего в индекс, определяется среднее арифметическое цен всех фьючерсных контрактов, срок которых истекает до конца девятого календарного месяца от текущей даты. Это означает, что индекс в зависимости от текущей даты охватывает 9 или 10 контрактных месяцев. [c.115]
ИНДЕКС АРИФМЕТИЧЕСКИЙ — относительный показатель изменения сложного экономич. явления,. вычисляемый в форме средней арифметич. взвешенной из относительных показателей изменения отдельных элементов этого явления (из т. н. индивидуальных индексов). Напр., формула И. а. объема реализованной про- [c.264]
Применение И. м. в с. позволяет решать задачи синтетического и аналитич. порядка, т. к. индексы выражают, с одной стороны, соотношения величин сложных экономич. явлений (сннтетич. значение), а с другой стороны — изменения общих итоговых показателей под действием определенных факторов. Напр., индекс цен выражает влияние изменения цен на изменение общей стоимости продукции (аналитич. значение). Применяя II. м. в с., следует различать содержание индекса и его форму. По содержанию различаются конкретные индексы объема продукции, себестоимости, цен, трудоемкости, производительности труда, объема работ и т. д. Цель исследования и характер изучаемого явления определяют содержание индекса. По форме вычислений различаются индекс агрегатный, индекс арифметический и индекс гармонический. f [c.267]
Индикаторы качества жизни. К интегральным индикаторам жизни относятся 1) индекс развития человеческого потенциала (ИРЧП) представляет собой среднюю арифметическую трех индексов ожидаемой продолжительности жизни (ОПЖ), уровня образования (УО) и ВВП на душу населения (ВВПн) в долларах, по паритету покупательной способности [c.110]
В зарубежной экономической литературе считается, что первый индекс цен был построен итальянским экономистом Джаном Ринальдо Карли в 1751 г. Этот индекс был построен по средней арифметической формуле без применения системы взвешивания. [c.554]
Предложен немецким экономистом Этьеном Лас-пейресом (1871). Широко применяется при расчете индекса потребительских цен. Представляет сравнение агрегированных цен, взвешенных по физическим объемам базисного периода или среднее арифметическое индексов, взвешенных по стоимости базисного периода [c.557]
В экономической литературе считается, что первый индекс цен был построен итальянским экономистом Карли в 1 764 г. Этот индекс был построен по среднеарифметической формуле без применения какой-либо системы взвешивания. В XIX веке при построении индексов цен, в основном по агрегатной или соответствующей ей среднеарифметической формуле, статистики начинают использовать систему взвешивания. В зависимости от выбора базисных или текущих весов возникли две формулы Ласпейреса (1871 г.) и Пааше (1874 г.). Более широкое практическое применение находят две другие их формы в формуле Ласпейреса — средняя арифметическая форма, в формуле Пааше — средняя гармоническая, которые отражены в табл. 16.1. [c.309]
Чтобы проверить индексы табл. 24, мы самостоятельно вывели из приведенных у А. Д, Поленова догубернских данных подесятинной оплаты средние (арифметические) коэффициенты по черноземной и нечерноземной полосам за все время, за которое к ним можно было получить сравнимые коэффициенты поденной оплаты из публикаций Департамента земледелия. Такое сопоставление оказалось возможным сделать за 1882— 1895 гг. по 48 губерниям Европейской России (без Курляндии и Таврической губернии). Попутно нам удалось выяснить, что у А. Д. Поленова фигурировала поденная оплата батрака-ж жадны. Мы же предпочли воспользоваться средней оплатой труда поденщиков обоего пола (на своих харчах), В результате получилось следующее сопоставление (табл. 25)18. [c.273]
Теория знает много средних — и арифметическую, и геометрическую, и т. п. Взвешивание этих средних можно тоже производить яо-разному. Все зависит от того, как поставить вопрос, па который должен ответить индекс. Мы его ставим так во сколько раз меньше рабочего времени потребовалось за отчетный период для производства продукции данного состава в сферах А и Б по сравнению с затратами предшествующего периода для получения продукции того же состава И если в отчетном периоде в сфере -А потребовалось t еднпиц рабочего времени, а в сфере Л — ti, то вполне точный ответ на наш вопрос представит средняя [c.426]
Колебания относительных приростов (темпов прироста) нашего показателя па Душу очень велики, заметно превышая даже сильную колеблемость (см. стр. 140) глобального показателя, именно коэффициент вариации по отношению к средней арифметической, к выравненной прямой и к параболе 2-го порядка соответственно равен 47,8 46,5 46,1%, т. с. колебания совсем не умеряются при выравнивании. Средний арифметический годовой темп прироста (цепной индекс) дохода на душу за весь исследуемый период составляет 5,0%. Если исчислить средний темп как среднегеометрическую по двум крайним членам исходного ряда темпов, то получим средний темп прироста, равный 5,32%. Если выравнять относительный прирост (темп) народного дохода па душу по прямой, то ежегодный прирост его составит 0,11%. Однако при отмеченной большой колеблемости этого ряда этот прирост темпа является в значительной степени иллюзорным, и при планировании относительного прироста народного дохода на-душу правильнее ориентироваться на постоянный темп, или постоянный относительный коэффициент прироста 5,1%, даваемый приведенным выше уравнением показательной кривой. [c.143]
FT-SE 100 - наиболее распространенный индекс в Великобритании, широко известный как footsie (Футси 100). Представляет собой взвешенный арифметический индекс, рассчитываемый на базе 100 крупнейших по рыночной капитализации компаний Великобритании на поминутной основе. На компоненты "Футси" приходится около 70% общей капитализации фондового рынка Великобритании. FT-SE Mid 250 - индекс акций компаний со средней капитализацией, на которые приходится примерно 20% рынка Великобритании. Это следующие 250 компаний после сотни крупнейших, входящих в индекс FT-SE 100. Рассчитывается с декабря 1985г. Япония [c.90]
Эти тенденции благоприятны для сторонников фундаментального анализа стоимости компаний, отраслей и секторов. Но это еще не все. В условиях длительного подъема рынка, начавшегося в августе 1982 г., внимание часто отвлекалось от отдельных компаний к рынку сертификатов на акции и к таким арифметическим конструкциям, как индексы, средние и композиты, которые сконструированы так, чтобы замаскировать или устранить индивидуальные различия между акциями. Большой объем ежедневных сделок, отражаемый в учетных книгах депозитарной трастовой компании, говорит об активной деятельности арбит-ражеров, об операциях со слишком большими для брокеров и дилеров пакетами акций, о хеджировании портфельных рисков и об избыточности усилий, направленных на контроль всех форм рыночного риска. Меньшая часть этой бешеной активности представляет собой инвестиционные операции, направляемые систематическим анализом и оценкой корпораций. [c.526]
Большинство трейдеров имеет только двух соседей, небольшое количество (первоначальные) имеет 2рсоседей, другие находятся где-то в промежутке между этими числами. Обратите внимание, что наименее связанные агенты имеют в 2F1 раз меньше соседей, чем те, которые имеют больше всего связей, которые сами имеют примерно в 2Р раза меньше соседей, чем всего существует агентов. Выведем среднее арифметическое по всем трейдерам и получим результат, что среднее расстояние между любой парой трейдеров пропорционально индексу итераций р, то есть логарифму числа вершин. [c.180]
