СТОХАСТИЧЕСКИЙ МЕТОД НАИСКОРЕЙШЕГО СПУСКА [c.155]
На основе метода была создана программа, с помощью которой было проведено численное исследование метода. Это исследование показало более высокую скорость сходимости, чем в методе Монте-Карло. На рис. 1.50 построены графики зависимости функционала J по итерациям алгоритма Монте-Карло и стохастического алгоритма наискорейшего спуска. Кривая 1 соответствует наиболее методу Монте-Карло в случае наиболее быстрого получения оптимального решения. Кривые 2 и 3 соответствуют методу наискорейшего спуска для различных значений а и Ь кривая 2 — а = 10, 6 = 10 кривая 3 — а = 20, Ъ = 2. [c.156]
| Рис. 1.50. Сходимость функционала в методе Монте-Карло (1) и методе наискорейшего спуска (2, 3) при решении задачи с га = 27 и р = 8 | 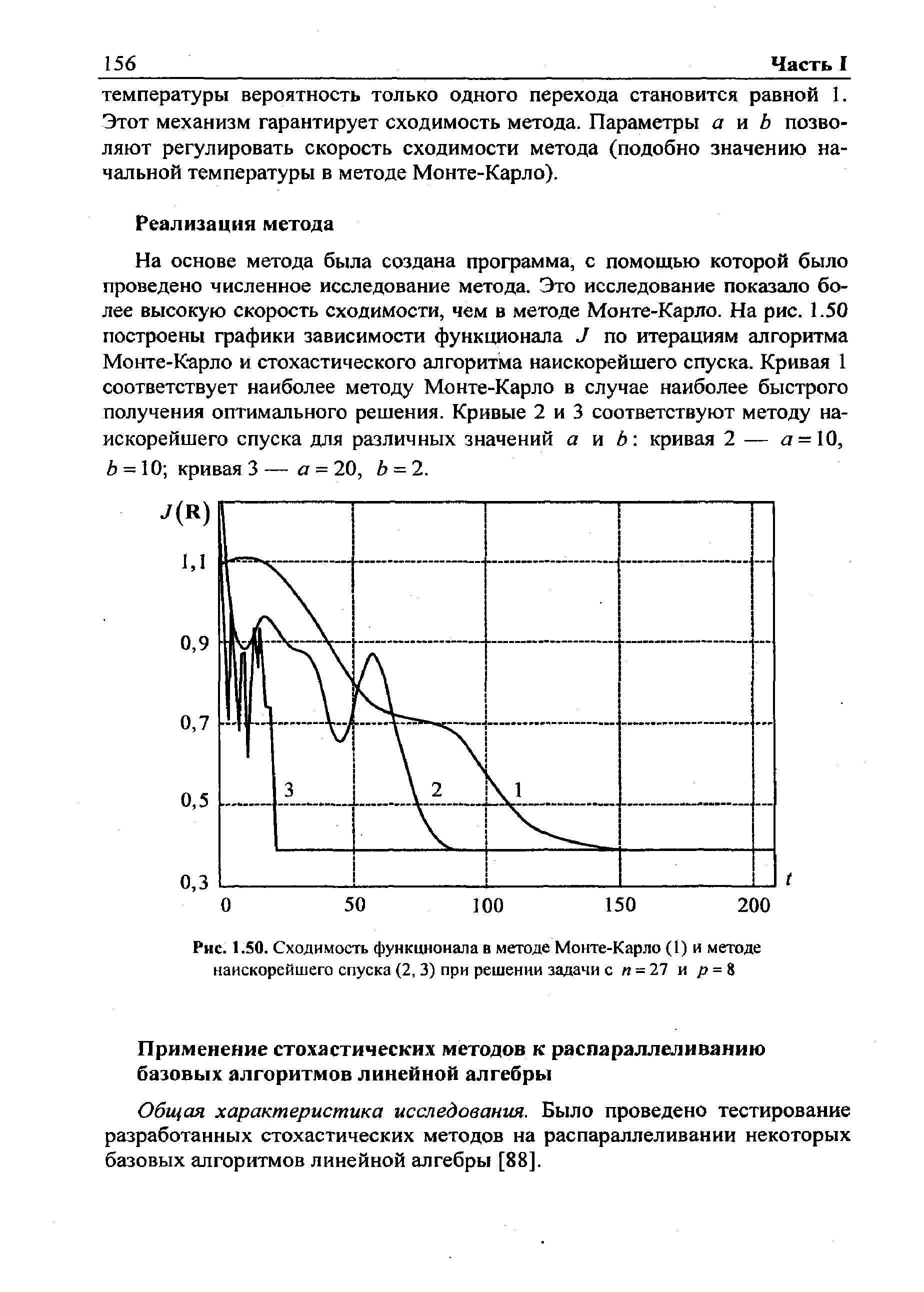 |
Эти утверждения вполне очевидны, и мы их доказывать не будем. Отметим лишь, что чем уже множество стационарных точек, тем надежнее метод поиска. С этой точки зрения предпочтителен случайный поиск. Однако с точки зрения эффективности предпочтительнее метод наискорейшего спуска. Не исключенная в принципе опасность застрять в точке перегиба маловероятна, так как такие точки являются неустойчивыми точками метода наискорейшего спуска, в отличие от точки локального минимума, являющейся устойчивой. [c.395]
Теперь мы докажем характерную теорему о сходимости метода наискорейшего спуска. Эта теорема, в частности, позволит уточнить требования к точности определения шага спуска s. Обозначим через R (у) область re-мерного пространства, определяемую условием х R (у) / (х) . / (у). Функцию / (х) будем считать гладкой (достаточно непрерывности вторых производных). [c.395]
Теорема. Пусть R (x°) — ограниченная замкнутая область, и f (х в R (х°) имеет лишь единственную точку х, в которой fx (х )=0 эта точка, таким образом, является единственной точкой локального минимума f (х) в R (x°). Тогда метод наискорейшего спуска, стартующий из точки х°, сходится к х. [c.395]
Значение W0(FS, Ts), соответствующее сбалансированному лимиту капиталовложений Ls, в рассматриваемой модели получается при реализации метода наискорейшего спуска с переменным шагом. Поиск выполняется до обеспечения неравенства вида [c.106]
Метод наискорейшего спуска [c.87]
Для нахождения шага А, в методе наискорейшего спуска требуется решить уравнение (2.13), которое может оказаться достаточно сложным. Поэтому часто ограничиваются подбором такого значения А,, что ср(А,) > q>(0). Для этого задаются некоторым начальным значением A,j (например, =1) и проверяют условие ф(Х1)>ф(0). Если оно не выполняется, то полагают [c.89]
Метод наискорейшего спуска и методы дробления шага. [c.107]
Для решения каких задач предназначены метод наискорейшего спуска и метод дробления шага [c.107]
Порядок "обхода" точек плана, т.е. самого проведения эксперимента. В экспериментах, предназначенных для отыскания оптимальных условий протекания некоторого процесса, применяются планы исследования поверхности отклика (реакции), основанные на методе наискорейшего роста (подъема), наискорейшего спуска, последовательные планы и др. [c.263]
О скорости сходимости метода спуска по градиенту. В общем случае трудно оценить скорость сходимости процесса наискорейшего спуска, каждый шаг которого состоит в решении задачи min / (х — sfx). Однако определенную [c.406]
Более точно градиент может быть вычислен, если известно линейное приближение поверхности отклика, полученное по числу точек, превышающему число переменных. Боксом и Уилсоном предложено определять градиент по линейному приближению поверхности отклика на основе дробного факторного эксперимента. Если градиент рассчитывается заново после каждого шага решения, то это метод градиента. Если же в направлении градиента выполняется несколько шагов до тех пор, пока не перестанем приближаться к оптимуму, то это метод крутого восхождения или наискорейшего спуска, [c.270]
В задачах на минимум движение происходит в сторону убывания функции, и такой метод носит название наискорейшего спуска. [c.353]
Поставлена задача отображения алгоритмов, представленных взвешенными графами большой размерности, на архитектуры мультитранспьютерных вычислительных систем, содержащих большое число транспьютерных элементов. Проведено теоретическое и численное исследование поставленной задачи. Исследование показало, что функционал, подлежащий минимизации, обладает ярко выраженной овражной структурой и содержит большое число локальных минимумов, что затрудняет и даже делает невозможным применение большинства методов решения подобных задач — различных эвристических методов, методов безусловного спуска, методов наискорейшего спуска и т.п. Единственной возможной альтернативой этим методам является использование стохастических алгоритмов. [c.165]
Разработан ряд стохастических методов решения поставленной оптимизационной задачи распараллеливания вычислений. В первом методе — стохастическом методе попарной оптимизации подграфов — поиск оптимального решения осуществляется за счет взаимного (стохастического) переноса вершин между различными парами подграфов графа алгоритма. Второй метод — метод Монте-Карло случайного блуждания вершин графа алгоритма по подграфам — основан на отождествлении вершин графа алгоритма с некоторыми частицами, совершающими случайные блуждания по областям-подграфам в потенциальном силовом поле, роль потенциала которого играет минимизируемый функционал. Наиболее вероятное состояние подобной системы частиц соответствует минимуму потенциала —-и, следовательно, является искомым решением. Поиск такого состояния осуществляется методом Монте-Карло с использованием специальной процедуры имитации отжига . Третий метод — стохастический метод наискорейшего спуска — основан на использовании дискретного аналога градиента минимизируемого функционала. Все разработанные методы реализованы программно и являются частью системы программ PARALLAX. Проведено тестирование созданных программ и сравнение их работы на простейших примерах. [c.166]
Энеев Т. М. Некоторые вопросы применения метода наискорейшего спуска. — М. ИПМ АН СССР, 1970, № 17. [c.483]
Для решения этой задачи существует два пути. Во-первых, может быть осуществлена непосредственная минимизация функции F с помощью методов нелинейной оптимизации, позволяющих находить экстремумы выпуклых линий. Это, например, метод наискорейшего спуска, при использовании которого в некоторой исходной точке определяется антиградиент (направление наиболее быстрого убывания) функции F. Далее находится минимум /"при движении в данном направлении, и в точке этого минимума снова определяется градиент. Процедура повторяется до тех пор, пока разница значений F на двух последовательных шагах не окажется меньше заданной малой величины. Другой путь состоит в решении системы нелинейных уравнений, которая получается из необходимых условий экстремума функции F. Эти условия - равенство нулю частных производных функции Fno каждому из параметров а., т.е. [c.360]
Хотя метод Монте-Карло, описанный в предыдущем пункте, и оказался пригодным к решению больших задач отображения алгоритмов на мультитранспьютерные ВС, его слабым местом является достаточно медленная сходимость. Попытки увеличить скорость сходимости за счет увеличения начальной температуры приводят к ухудшению стационарного решения. В силу этого был разработан новый стохастический алгоритм наискорейшего спуска. В этом методе, так же как и в методе Монте-Карло, используется процедура имитации отжига, чтобы гарантировать сходимость метода. Общая схема метода такова. 1. Полагаем начальную температуру равной Q = а. [c.155]
Из второй группы методов применительно к определенным задачам используются градиентный, наискорейшего спуска, покоординатного спуска, релаксационный, динамического программирования, метод ветвей и границ. Рассмотрим кратко применение градиентного метода для оптимального распределения элек--трической нагрузки. При использовании других методов алгоритм изменяется главным образом в отношении условий и способов выбора направления, а также величин шага итерации. [c.156]
Метод градиентного спуска. Поскольку антиградиент — f (xi ) указывает направление наискорейшего убывания функции f(x), то естественным является перемещение из точки Х по этому направлению. Метод спуска, в котором sjt=/ (Xi) называется методом градиентного спуска. Если Ак= 1, то релаксационный процесс называется методом скорейшего спуска. [c.177]
Смотреть страницы где упоминается термин Метод наискорейшего спуска
: [c.473] [c.398] [c.407] [c.360] [c.89] [c.89] [c.59] [c.210] [c.137]Приближенное решение задач оптимального управления (1978) -- [ c.395 ]
