Необходимо отметить, что для ЛПР представляет интерес реализуемость той или иной альтернативы в конкретной планово-производственной ситуации. С математической точки зрения, реализуемость альтернативы определяется совместностью или несовместностью системы ограничений. ЛПР приходится решать двоякую задачу 1) распознать производственную ситуацию 2) оценить реализуемость альтернативы. [c.202]
| Рис. 1.10. Сообщение при несовместной системе ограничений задачи | 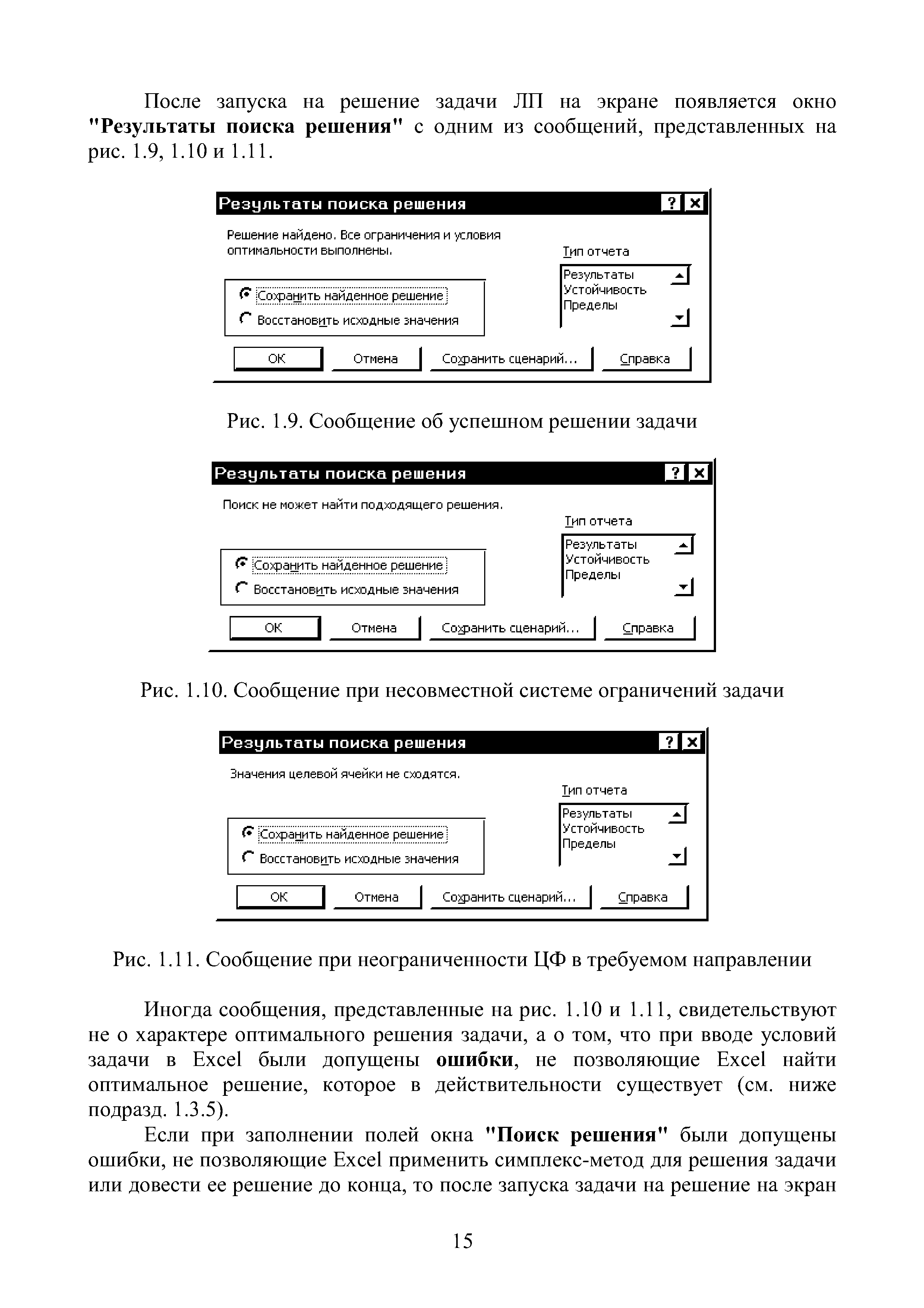 |
Каждое из неравенств задачи ЛП (1.1) определяет на координатной плоскости (х ,Х2) некоторую полуплоскость (рис. 2.1), а система неравенств в целом — пересечение соответствующих плоскостей. Множество точек пересечения данных полуплоскостей называется областью допустимых решений (ОДР). ОДР всегда представляет собой выпуклую фигуру, т.е. обладающую следующим свойством если две точки А и В принадлежат этой фигуре, то и весь отрезок АВ принадлежит ей. ОДР графически может быть представлена выпуклым многоугольником, неограниченной выпуклой многоугольной областью, отрезком, лучем, одной точкой. В случае несовместности системы ограничений задачи (1.1) ОДР является пустым множеством. [c.28]
Опыт решения задач планирования показывает, что при назначении плановых заданий система ограничений, описывающих НЛП, часто оказывается несовместной. [c.206]
Совместность системы ограничений — обязательное условие разрешимости модели в случае несовместности этой системы допустимое множество является пустым. [c.237]
В системах моделей различаются общесистемные (или глобальные) О.м., имеющие силу для всей моделируемой экономической системы, и локальные ограничения для моделей отдельных подсистем. Несовместность локальных ограничений с общесистемными приводит к неразрешимости системы моделей. [c.238]
На рис. 7.3 изображен случай, когда максимум недостижим, а на рис. 7.4 — случай, когда система ограничений задачи несовместна. Отметим, что нахождение минимального значения Z при данной системе ограничений отличается от нахождения ее максимального значения при тех же ограничениях лишь тем, что линия уровня Z передвигается не в направлении вектора С = ( j 2), а в противоположном направлении. Таким образом, отмеченные выше случаи, встречающиеся при нахождении максимального значения целевой функции, имеют место и при определении ее минимального значения. [c.204]
В дальнейшем без ограничения общности можем предполагать, что число уравнений, задающих множество Д меньше или равно числу переменных задачи (т < п). Действительно, если это не так, то либо система уравнений Ах = b несовместна (и, значит, множество D пустое), либо содержит избыточные (линейно зависимые) уравнения. [c.30]
В задачах оптимального планирования нефтеперерабатывающих производств система ограничений (2.18) является смешанной и включает как равенства, так и неравенства. В совместной системе в конечном счете все искусственные переменные должны быть выведены из начального базиса. При решении задач с фиксированными коэффициентами несовместность системы ограничений, которая в принципе может быть устранена учетом условий варьируемости, может выявиться на некоторой г-й итерации. Предыдущие - 1 итерации могут считаться эффективными, поскольку они обеспечили вывод из начального базиса соответствующего числа искусственных переменных. Данное обстоятельство и может быть использовано для улучшения эффективности расчетной процедуры. [c.33]
Необходимо отметить, что содержание работ по формированию моделей и их предоптимизационному анализу в литературе освещено недостаточно. Нам представляется, что именно по этой причине не удается решить проблему тиражирования моделей и пакета прикладных программ. Так, например, получившие наибольшее распространение линейные модели не всегда удается реализовать с помощью пакетов LPS/360 или ЛП АСУ однократным вводом исходных данных в ЭВМ. Большая размерность задач (до нескольких тысяч переменных и ограничений) и специальная форма используемых при этом ограничений не позволяют визуально, до решения ее, определить разрешимость принятой системы ограничений. Несовместность исходных условий при принятых значениях соответствующих параметров обнаруживается только после решения. [c.143]
Опираясь на теорему 6.1, можно выделить классы матриц, для которых из условий (6.1) вытекала бы неразрешимость исходной задачи (например, несовместность системы ее ограничений). Одним из таких классов является класс коположительных-плюс матриц, другим — уже упоминавшийся класс строчно-достаточных матриц. [c.23]
