Для прогноза /Q можно использовать выражение (9.141), разрешив его относительно Ь и найдя Ъ и Щ из равенств (9.145). Использование квадратичной аппроксимации /Q почти не осложняет расчеты, но в ряде случаев уменьшает время решения задачи (9.149) за счет более разумного выбора коэффициента штрафа Л. [c.364]
М (и, X, а) = / причем коэффициент штрафа а уже не обязательно должен быть [c.462]
Замечание. Иногда М. Ф. Л. вводится и интерпретируется несколько иначе. В обычной методике штрафных функций с не очень большими коэффициентами штрафа не удается получить хорошее выполнение условий / (и)=0. Для того чтобы усилить сходимость процесса, не увеличивая коэффициента штрафа, задачу заменяют другой, сдвигая требуемые значения /,. (и). Пусть в процессе поиска получена какая-то точка и, в которой/ (м ) =0 и в окрестности которой дальнейшая эволюция и происходит слишком медленно. Тогда задача изменяется вместо условий / (и)=0 ставятся условия / (и) = —13/ (и ), где 3 — некоторый множитель. Тогда функция / (и) (3) метода штрафных функций превращается в [c.468]
Графически функция прибыли (3.3.11) представлена на рис. 3.3 при разных значениях коэффициента штрафов [c.68]
Вид функции штрафа подобран таким образом, чтобы максимально упростить нахождение значений коэффициента штрафа а,, обеспечивающего в точке максимума функции /, по переменным, характеризующим состояние элемента, совпадение A.J и q. Выбор функции штрафа другого вида, например линейной функции штрафа X ( -ь 9i) = j К- — 1ц , несколько усложняет определение таких значений оц. [c.91]
| Рис. .Н. Геометрическое представление множеств механизмов функционирования с различными степенями централизации в пространстве коэффициентов штрафа за невыполнение плана. | 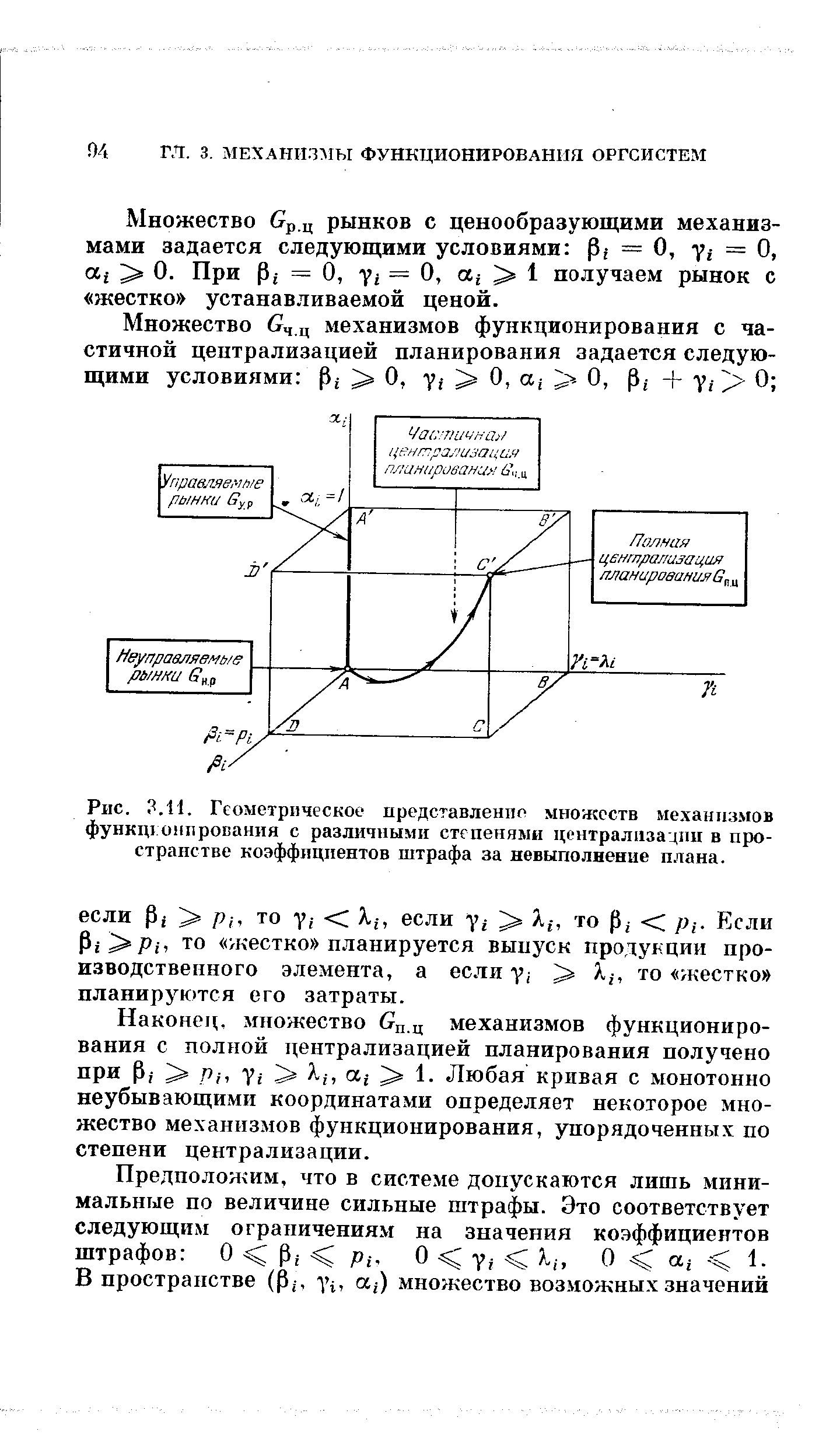 |
Привлекательность кусочно-линейных функций штрафа с практической точки зрения объясняется их предельной простотой. Для задания таких функций штрафа достаточно задать коэффициенты штрафов а и рг/. На практике часто эти коэффициенты принимаются одинаковыми для всех элементов системы, и тем самым задание функций штрафа еще более упрощается. [c.161]
Кусочно-линейная функция штрафа %i (Ai -) (4.12.3) является монотонно неубывающей функцией на полуосях Д,-/ и вогнутой при следующем соотношении коэффициентов штрафа [c.162]
К таким доходам относятся а) прибыль от эксплуатации жилищного и коммунального хозяйства б) поступления списанных безнадежных долгов в) полученные штрафы, пени, проценты и судебные издержки сверх уплаченных г) превышение скидок с тарифа над надбавками к тарифу на электроэнергию за коэффициент мощности электроустановок д) прибыль прошлых лет, выявленная в отчетном году е) прочие прибыли. [c.273]
Используются прямые и косвенные показатели ритмичности. Прямые показатели - коэффициент ритмичности, коэффициент аритмичности, удельный вес производства продукции за каждую декаду к месячному выпуску, удельный вес произведенной продукции за каждый месяц к квартальному выпуску, удельный вес продукции, выпущенной за первую декаду месяца, к третьей декаде предыдущего месяца. Косвенные показатели - оплата простоев, сверхурочные работы, уплата штрафов за недопоставку и несвоевременную отгрузку продукции, наличие сверхнормативных остатков незавершенного производства и готовой продукции на складах. [c.247]
Целевая функция представляет сумму штрафов , налагающихся за неполное обеспечение потребителей фондами. Коэффициенты dA определяют значение штрафа за одну единицу необеспеченного фондами ресурса. [c.147]
На основе результатов предварительного анализа параметры модели, определяющие объемы перерабатываемых ресурсов, выпуск готовой продукции, производительности технологических установок и процессов, коэффициенты отбора нефтепродуктов, в зависимости от величины вариации принимаются детерминированными или случайными. Ограничения на математические ожидания невязок стохастических условий задачи выбираются в зависимости от вероятностных характеристик случайных величин с учетом рекомендаций экспертов-технологов и работников планового отдела предприятия. Аналогичным образом устанавливаются штрафы за коррекцию решения задачи. Для НПП топлив-но-масляного профиля задача календарного планирования включает порядка 1400 переменных, 940 уравнений, 300 верхних и 280 нижних граничных условий. Коэффициент заполненности матрицы условий задачи равен 0,21. [c.178]
К расходам непроизводительного характера, включаемым в состав общезаводских расходов только в учете, относятся штрафы, пеня, неустойки за невыполнение условий перевозок и договоров, надбавки к тарифам на электроэнергию за низкий коэффициент использования мощности электроустановок потери, порча и недостачи материалов, продукции на заводских складах и др. [c.247]
В результате малые коэффициенты убывают быстрее, чем большие. Кроме того, уменьшение весов помогает уходить с плоских участков поверхности на ранних стадиях обучения. Были предложены и другие виды выражений для штрафа, в результате чего удаляются не только соединения, но и нейроны (см. [132], [64]). Еще один метод уменьшения числа связей — минимизация вреда для мозга (см. [174]). Цель его состояла в том, чтобы находить в сети те веса, которые можно удалить, не меняя существенно среднеквадратичную ошибку (MSE) на обучающем множестве. Вводится показатель s, (так называемая выпуклость веса) по формуле [c.36]
Здесь технологический коэффициент а учитывает все текущие затраты основного производства (стоимость оборотных фондов, среднюю зарплату персонала и т.д.) S(t, ) — функция штрафа за загрязнение N = N(t) — темп налоговых отчислений Р = P(t) — темп непроизводственного потребления А — функция, задающая правила финансовых взаимоотношений предприятия с Центром и другими предприятиями в природоохранной деятельности (различные варианты этой функции будут рассмотрены отдельно). [c.29]
В. Монотонное нробразованне функции цели с введением квадратичного штрафа. По тем же сооброжениям, что и для модифицированной функции Лагранжа, введем векторный коэффициент штрафа и запишем R в форме [c.364]
Формально метод штрафных функций решает все проблемы, однако при практической его реализации встретились серьезные трудности медленная сходимость, ненадежность и грубость результатов. Причины этих неприятностей были поняты, и сторонники метода сосредоточили свои усилия на решении соответствующих вопросов вычислительной технологии разработке надежных и эффективных методов поиска минимума для очень сложных, негладких, с оврагами и хребтами функций, методам подбора коэффициентов штрафа и тактике их изменения в процессе решения задачи. Эта работа продолжается, и в настоящее время ее перспективы еще не ясны. Идея метода штрафных функций имеет своих сторонников, которые надеются преодолеть технические сложности минимизации штрафного функционала. Одновременно начало развиваться и другое направление, в котором либо совсем не используют штрафных функций, либо стараются учесть методом штрафа как можно меньше условий. Разумеется, это потребовало определенного сужения класса задач. Легко были построены алгоритмы для задач, в которых имеется только ограничение и (t) U, а интегральных дополнительных условий (в частности, условий на х (Т)) нет. В этом случае после вычисления градиента w0 (t) образуется семейство и (s, t)=Pu [и (t) — Su>0 (t)], где Ри — оператор проектирования на U (в конечномерном пространстве). Далее S находится так же, как в простейшей задаче. Такие (или, в сущности, очень близкие) алгоритмы были предложены (под разными названиями) многими и применялись в расчетах (см., например, [43], [44]). [c.111]
Таким образом, система стимулирования с сепара-бельными кусочно-линейными функциями штрафа, коэффициенты штрафа которых удовлетворяют условиям [c.163]
Аудитор, следовательно, должен промоделировать возможные последствия таких ситуаций (и их конкретного вариантного расклада) в условиях действующей налоговой системы. В случаях (а) и (б) могут быть применены соответствующие коэффициенты, штрафы, пени и т.д. Такие обстоятельства он обязан отразить в заключении, поскольку они могут привести даже к банкротству клиента. В случае (в) он может лишь устно обсудить проблему с администраций, найти для нее вполне легитимные возможности защиты прав проверяемого клиента и подобрать для него соответствующую формулировку, используемую в абзаце с оговорками. [c.516]
Рис. 7.4 показывает результат, минимизирующий издержки. На вертикальной оси откладывается использование фирмой капитала в машино-часах, а на горизонтальной оси показывается объем промышленных сбросов воды в галлонах. Рассмотрим вначале, как осуществляется производство на фирме, когда штраф за вредные сбросы отсутствует. Точка А представляет такое сочетание капитала и объема промышленных вод, которое позволяет фирме производить 2000 т металла в день при минимальных издержках. Так как фирма минимизирует издержки, А лежит на изокосте ВС, которая соприкасается с изо-квантой. Угловой коэффициент изокосты равен —10 долл./ 40 долл. = — 0,25, так как единица капитальных затрат стоит в 4 раза дороже единицы объема промышленных вод. [c.206]
