Метод сложного процента. Функции сложного процента. Накопленная сумма денежной единицы (будущая стоимость единицы). Накопление денежной единицы за период. Фактор фонда возмещения. Текущая стоимость денежной единицы. Текущая стоимость аннуитета. Взнос на амортизацию денежной единицы (ипотечная постоянная). Финансовые таблицы (таблицы функций сложного процента). [c.367]
Если положить РМТ — 1, т. е. будем вычислять текущую стоимость аннуитета единицы, то мы получим формулу вычисления фактора пятой функции [c.321]
Очевидно, что взнос на амортизацию единицы есть величина, обратная фактору пятой функции (текущей стоимости аннуитета единицы) [c.325]
Если в течение каждого базового периода денежные поступления происходят очень часто, так что промежутки между последовательными поступлениями представляют собой бесконечно малые величины, то аннуитет считают непрерывным, т.е. денежные поступления происходят непрерывно с постоянной интенсивностью одно и то же количество денежных единиц в единицу времени. [c.293]
Экономический смысл FM3(r,n), называемого мультиплицирующим множителем для аннуитета, заключается в следующем он показывает, чему будет равна суммарная величина срочного аннуитета в одну денежную единицу (например, один рубль) к концу срока его действия. Предполагается, что производится лишь начисление денежных сумм, а их изъятие может быть сделано по окончании срока действия аннуитета. Множитель FM3(r,n) часто используется в финансовых вычислениях, и поскольку легко заметить, что его значения в общем виде зависят лишь от г и п, они также табулированы. [c.75]
Экономический смысл FM4(r,n), называемого дисконтирующим множителем для аннуитета, заключается в следующем он показывает, чему равна с позиции текущего момента величина аннуитета с регулярными денежными поступлениями в размере одной денежной единицы (например, один рубль), продолжающегося п равных периодов с заданной процентной ставкой г. Значения этого множителя также табулированы. [c.75]
При расчете чистой текущей стоимости применяется функция текущего аннуитета — /4 (формула (16.7)) при равномерном распределении дохода по годам или функция текущей стоимости единицы — /з (формула (16.5)), примененная к каждому элементу потока поступлений от инвестиций, суммированных за прогнозируемый период. [c.425]
Накопленная сумма единицы (колонка 1) Накопление единицы за период (колонка 2) Текущая стоимость аннуитета (колонка 5) Текущая стоимость единицы (колонка 4) Фактор фонда возмещения (колонка 3) Взнос на амортизацию единицы (колонка 6) [c.159]
Год Будущая стоимость единицы Накопление единицы за период Фактор фонда возмещения Текущая стоимость единицы Текущая стоимость единичного аннуитета Взнос за амортизацию единицы [c.164]
| Табл. 2. Приведенная стоимость ординарного аннуитета денежной единицы продолжительность п периодов | 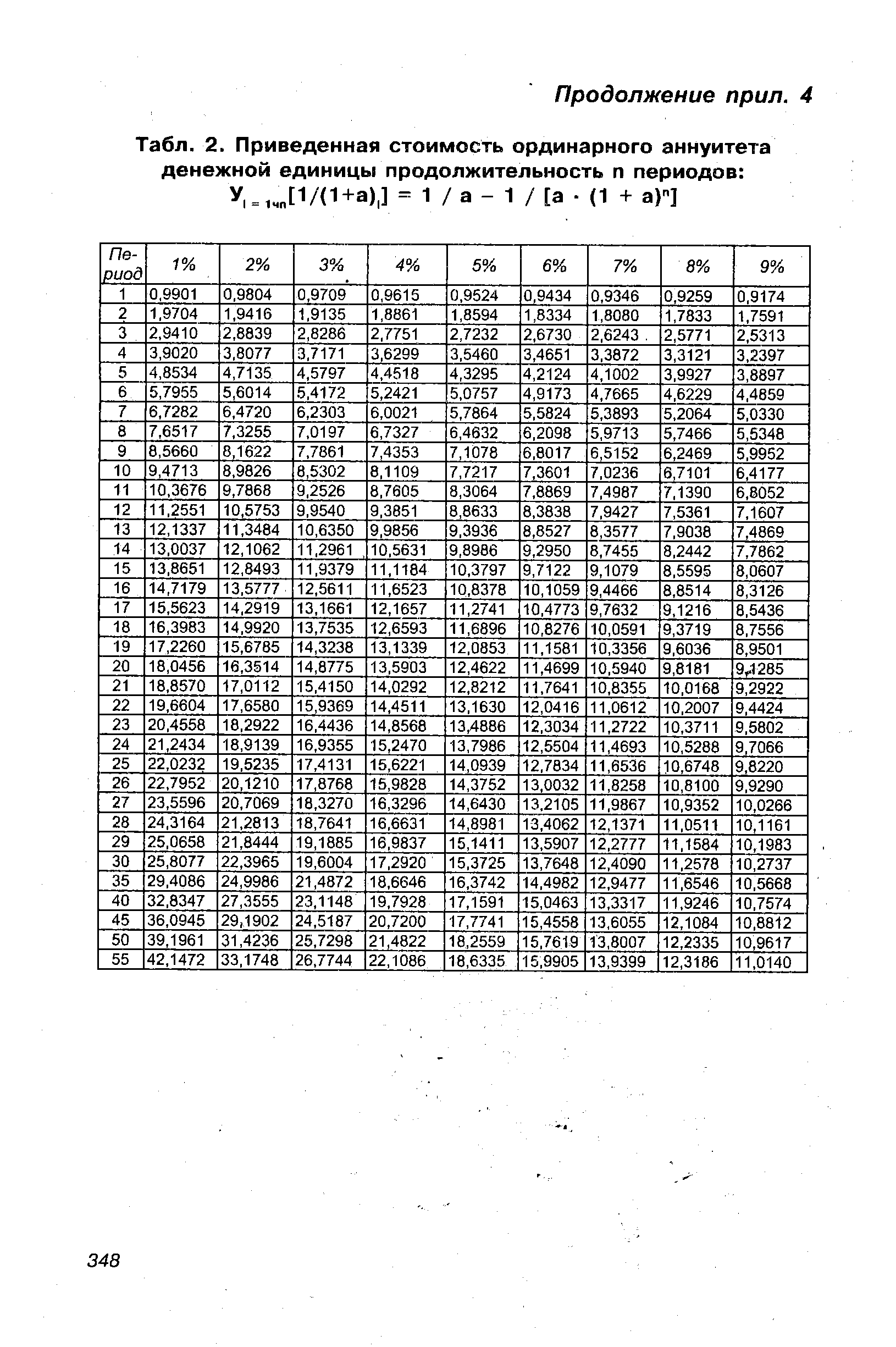 |
В (я, г) = [1-(1 + / )- ]//-, где В — приведенная стоимость аннуитета в одну денежную единицу п — количество периодов, когда возникают денежные потоки. [c.107]
На практике часто встречаются инвестиционные проекты, денежные потоки от которых поступают неравномерно, однако для оценки таких проектов во многих случаях желательно определить, какому воображаемому аннуитету эквивалентен данный инвестиционный проект. Зная аннуитет величиной в одну денежную единицу, это можно сделать при помощи следующей формулы [c.107]
Чтобы определить аннуитет, которому эквивалентен данный инвестиционный проект, рассчитаем сначала приведенную стоимость аннуитета на 5 лет величиной в одну денежную единицу при выбранной ставке дисконтирования (10%) [c.108]
Snr — будущая (наращенная) стоимость единичного аннуитета (аннуитета, все платежи которого равны одной денежной единице) [c.258]
При уровне выпуска х в 1 единицу продукции в год начиная с некоторого заданного Т производство должно продолжаться в течение одного года для получения общего объема V, равного 1, в течение двух лет — для получения 2, трех лет — для получения 3 единиц и т.д. (см. таблицу). При уровне выпуска, равном 2 единицам в год, производство должно продолжаться один год для получения 2 единиц общего объема продукции, два года для получения 4 единиц и т.д. Сегодняшняя ценность затрат при уровне выпуска x(t), равном 2 единицам в год, для общего объема V, равного 4, за два года будет 330 дол. (что при 6% составит двухгодичный аннуитет 180 дол.). [c.141]
Экономический смысл FM3(r,n), называемого мультиплицирующим множителем для аннуитета, заключается в следующем он показывает, чему будет равна суммарная величина срочного аннуитета в одну денежную единицу (например, один рубль) к концу срока его действия. Предполагается, что производится лишь начисление денежных сумм, а их изъятие может быть сделано по окончании срока действия аннуитета. Мно- [c.37]
Заметим, что после получения эквивалентного простого аннуитета единицей времени становится период начисления процентов. [c.98]
Решение. Здесь общий полагающийся аннуитет должен быть заменен другим общим полагающимся аннуитетом. Это производится сначала заменой данного аннуитета на обыкновенный простой аннуитет, выплачиваемый поквартально, а затем преобразованием простого аннуитета в общий полагающийся аннуитет, выплачиваемый ежемесячно. Для первого этапа решения возьмем пять лет как основную единицу измерения времени вместо одного года. Тогда р = 1 и т = 20 [c.207]
Рассмотрим ситуацию, в которой корпорация планирует выплачивать дивиденд D в конце текущего периода. Предположим, прогнозируется, что дивиденды увеличиваются согласно геометрической прогрессии ориентировочно с общим знаменателем 1 + k и акция приобретается для того, чтобы давать доходность i за период, где -1
ЕДИНИЦА НАКОПЛЕНИЯ -доля фонда коллективного аннуитета, которая определяется путем деления общей суммы фонда на количество единиц накопления. Используется в период накопления аннуитета. [c.205]
Коэффициент аннуитета показывает размер постоянныхежегодт ных платежей, современная стоимость которых равна денежной единице, для заданного количества лет (и) при заданной процентной ставке (г). [c.600]
Величина F может быть теперь найдена методом, использованным в главе 4. Если мы добавим единицу к общему аннуитету и его эквивалентной стоимости в конце шестнадцатогого года (64-го периода начисления) и выпишем уравнение эквивалентности на эту дату, то получим [c.219]
