| Таблица 1. Дискретизация состояний нейронов скрытого слоя |  |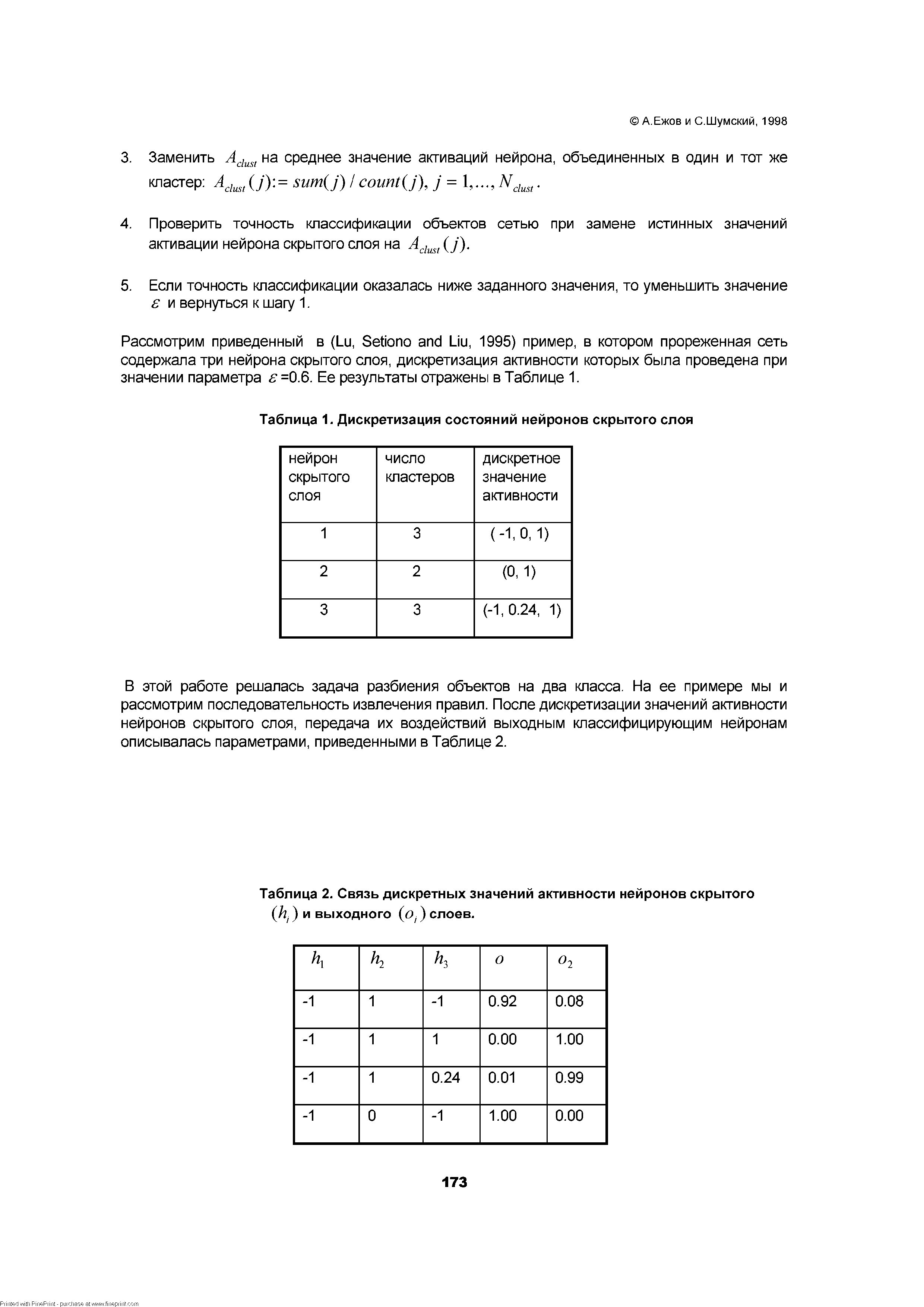
Определение коэффициента угрозы краха. Симуляция с использованием компьютерной программы идет следующим образом. Во-первых, мы выбираем дискретизацию времени с шагом St. Затем, зная величину случайных блужданий W(t-St) и цену B(t-8t) в предшествующее время t-dt, мы выводим W(t), прибавляя приращение, взятое из центрированного гауссова распределения с вариацией St. Отсюда мы выводим цену B(t), взяв величину, обратную (W -W(t))a, где - положительный показатель степени, определенный в модели. Затем мы выражаем, при условиях отсутствия арбитража и рациональных ожиданиях, вероятность h(t) возникновения краха во время следующего временного этапа, где h(t) - коэффициент угрозы краха. Мы сравниваем данную вероятность со случайным числом гаи, равномерно выбранным в интервале [0,1] и запускаем механизм краха, если ran < h(t)St. В данном случае цена B(t) меняется на B(t)(l-K), где к взято из предварительно выбранного распределения. Например, спад к при крахе может быть зафиксирован на уровне, скажем, 20%. Слишком прямолинейно сводить это к арбитражному распределению скачков. После краха динамика продолжается с бесконечно малым приращением, как и раньше, начиная с этого нового значения для времени t, после соответствующего переноса W(t), чтобы обеспечить непрерывность цен. Если ran > h(t)St, краха не происходит и динамика повторится на следующем временном шаге. [c.171]
Задавшись приемлемым уровнем дискретизации по а на интервале [c.70]
Широкое разнообразие и многоплановый характер задач управления систем требуют, соответственно, применения разнообразных математических методов. Однако при всем многообразии задач и методов их решения можно выделить три основные группы моделей. К первой группе относятся дискретные модели, построенные на основе дискретизации пространственных и временных координат. Дискретные модели, обладающие достоинствами численных методов, наиболее универсальны допускают возможность достаточно наглядной интерпретации результатов обладают определенной [c.86]
Уровень дискретизации деления структуры зависит от двух взаимосвязанных факторов. Первый из которых, состоит в наличии технологий, позволяющих автоматизировать функционирование новой структуры. Второй — в стремлении получения модели, обладающей более высоким уровнем прозрачности, гибкости управления и динамичностью, необходимой в решении часто меняющихся приоритетов и задач. [c.44]
Дискретизация непрерывных переменных 226 [c.464]
Из тех же соображений характеристики временной дискретизации состояния объекта управления и управляющей системы, как правило, отождествляются по величине, а моменты изменения состояния имеют некоторый временной сдвиг относительно [c.87]
Наряду с моделями и их информационным обеспечением в систему эколого-экономических расчетов должны входить разнообразные методы анализа этих моделей и решения на них различных задач, реализованных в виде отдельных программ или пакетов прикладных программ. К ним относятся методы идентификации моделей, методы преобразования моделей к виду, более удобному для последующего анализа, в частности, дискретизация и агрегирование, методы параметрического и статистического анализа, методы получения оптимальных решений и нормирования воздействий для различных классов задач, специальные методы и др. [c.176]
Задавшись приемлемым уровнем дискретизации на интервале принадлежности [0,1], можно реконструировать результирующее нечеткое число МРУ (ЧДД) путем аппроксимации его функции принадлежности ломаной кривой по интервальным точкам. Часто оказывается возможным привести NPV к треугольному виду, ограничиваясь расчетами по значимым точкам нечетких чисел исходных данных. Это позволяет рассчитывать все ключевые параметры в оценке степени риска не приближенно, а на основе аналитических соотношений. [c.19]
При генерировании случайных величин по нормальному закону с параметрами N(0,1) семь интервалов будут соответствовать примерному соотношению Дх = ст. В этом случае эмпирическая энтропия стремится к постоянному числу Я = 1п- /2ле, что уменьшает погрешности дискретизации непрерывного распределения. Проверка гипотезы проводилась с помощью критериев согласия Пирсона и Колмогорова-Смирнова. При проверке по Х2-критерию вычислялась критическая статистика [c.21]
Состояние подсистемы описывается множеством фазовых переменных, относящихся или к переменным потока, или потенциала. Множество фазовых переменных для каждой подсистемы конечно. В этом проявляется дискретизация пространства при переходе к макроуровню. [c.181]
Прежде чем строить графики с помощью баров или японских свечей необходимо договориться о дискретизации времени. Дело в том, что каждый бар или свеча представляют историю за определенный интервал или период времени. Эта история представляется теми же самыми четырьмя ценами, но примененными непосредственно к началу этого интервала (открытие, О), к максимальному и минимальному значениям (максимум, Н минимум, L) и к соответствующему окончанию интервала (закрытие, С). Сам интервал может быть при этом любой — неделя, месяц, квартал. Или день, час, полчаса, 5 минут, 1 минута и т.д. В зависимости от выбора длительности интервала график называется дневным (интервал времени — один день), часовым , недельным , пятиминутным и т.д. [c.150]
Произведем дискретизацию управления с шагом А . Дискретный аналог задачи [c.216]
Учесть в расчетах произвольные состояния внешней среды невозможно, да и не нужно. Каждый параметр обладает естественным уровнем дискретизации, который определяется точностью фиксации уровней показателей. Ее задает сам исследователь, исходя из поставленных целей и разумно ограничивая размерность модели. Точность задания возможных состояний среды должна убывать с течением времени. [c.262]
Эта нерегулярность вносит определенные трудности для применения уже имеющихся методов статистического анализа данных. Поэтому, как правило, статистические данные сначала подвергаются некоторой предварительной обработке (дискретизация, отбраковка аномальных наблюдений, сглаживание, выделение трендовых составляющих и т.п.). [c.392]
Остановимся подробнее на приемах дискретизации. [c.392]
Другой, широко распространенный метод дискретизации состоит в том, что сначала кусочно-постоянный процесс [c.393]
Затем проводится дискретизация этой модификации 5 = (St) так, как это описано выше в простейшем методе, т. е. образуется последовательность 5Л = (Stk) в точках tk = kA, k — 0,1,..., с параметром А, определяющим тот временной интервал (месяц, неделя, день, 20 мин., 5 мин.,...), который интересует инвестора, трейдера,.... [c.393]
В-пятых, цифровая модель вынуждена быть псевдо-точной. С одной стороны каждое число - исключительно точное понятие с другой стороны, при создании модели требуется делать постоянные приближения и округления. Чем выше степень дробления (дискретизации), тем меньше погрешность, и наоборот. [c.108]
Развитые в прежних работах автора для теоретического рынка опционов принципы построения оптимального портфеля инвестора со своим взглядом на свойства рынка используются для реального рынка опционов. Предлагаются два способа. Первый из них дает представление оптимального портфеля инвестора на континуальном однопериодном рынке опционов, которое далее применением процедуры дискретизации преобразуется к виду, пригодному уже для реального рынка. Второй подход дает представление оптимального портфеля инвестора непосредственно на основе дискретных страй-ков рынка опционов. В соответствии с ним разрабатывается согласованная с континуальным критерием VaR процедура, использующая для построения приближенно оптимального портфеля инвестора рыночные цены опционов. [c.2]
Рассмотрим приведенный в (Lu, Setiono and Liu, 1995) пример, в котором прореженная сеть содержала три нейрона скрытого слоя, дискретизация активности которых была проведена при значении параметра е =0.6. Ее результаты отражены в Таблице 1. [c.173]
Стандартизация. Стандартизация психологических тестов представляет собой линейное преобразование тестовых оценок, смысл которого заключается в замене исходных оценок новыми, производными, облегчающими понимание и интерпретацию тестовых результатов. Обычно используют два основных вида преобразовательных оценок приведение их к центронормированному виду и дискретизация. [c.81]
Интегрирование (2.2.2) проводится численно в декартовой прямоугольной системе с применением метода фиктивных областей. Для дискретизации по времени используется схема Кранка-Николсона и двуциклический метод многокомпонентного расщепления [Марчук, 1989] [c.93]
Для любого решения Р°(и, t) в форме (9.53) можно построить последовательность ui(t решений задачи (9.48), (9.49) следующим образом разобьем [0, г] на г интервалов AI, A2,. .., Аа- и примем на каждом из интерволов 7 (0 и u"(t) постоянными. Пусть для r-го интервала их значения равны 7 г и и1 (у — 0,. . . , т). Полученную при этом задачу назовем дискретизацией задачи (9.50), (9.51). [c.325]
Информационный подход, базирующийся на принципах дискретизации и разнообразия, дает возможность выделить главное, существенное в сложных технических системах. В работе [74] определяются информационные основы управления технологическими процессами с учетом потенциальных возможностей объекта как источника и как канала передачи информации. Вопросы применения теории управления на основе теории информации в организации систем автоматического контроля рассматриваются в работах [28, 55, 70, 78]. В работе [108] интуитивное понятие "качества" обобщается и численно оценивается через энтропию Шеннона. Синтез байесовского подхода и принципа максимума энтропии рассматривается Б.А. Абдрашидовым [1]. [c.16]
Описанный итеративный процесс представляет собой процедуру сокращения различных типов ошибок. К ним относятся, по крайней мере, следующие [20 — 221 а) общая ошибка дискретизации и конечности б) ошибка от выбора авторегрессивного процесса первого порядка в) ошибка применения частично асимптотических результатов к условиям малых выборок г) ошибки первоначальной оценки я(1) из-за несоблюдений условий (22) — (23), т. е. разницы между оценками инструментальных переменных и наибольшего правдоподобия д) дополнительной ошибки предварительной фильтрации данных в (25), возникающей вследствие изменения метрики под влиянием авторегрессивного преобразования и особенно ощутимой на низких частотах (область кратко- и среднесрочного прогноза) е) ошибки от предположения q = v = 0. [c.77]
Обратите внимание на вырожденность временнбй сетки по существу, [О, Т] разбит только на два счетных интервала, остальные — практически нулевые. Этот же дефект имеет решение второго варианта задачи ([77], таблица на стр. 151). Никакого отношения к решению дифференциальных уравнений табличные функции не имеют. Любопытно, что одно из таких решений было проконтролировано расчетом с N=20, получено совпадение по функционалу с точностью до 0,15%, и можно утверждать, что ошибка дискретизации является допустимой для практики ([77], стр. 151). Это совпадение связано, видимо, с тем, что и сетка с N=20 столь же вырождена и состоит из тех же двух счетных интервалов. 2 Содержательное обсуждение подобных решений бессмысленно, здесь нельзя даже говорить о какой-то, пусть не очень высокой, точности. Характерноз что используемый метод полностью обосяо- [c.310]
| Рис. 4.29. Схема аналогово-цифро-вого преобразования a — аналоговое представление сигнальной функции y=f(z) б — разбиение оси абсцисс на равные отрезки, соответствующие минимальному пределу разрешения z в — дискретизация амплитуд и кодирование в двоичной форме г — цифровое выражение сигнальной функции в двоичном представлении. |  |
Модель Шмидта(38)имееттакжетупривлекательность,чтоее "дискретизация" позволяет естественным образом получать дискретные модели эволюции процентных ставок, воспользовавшись той или иной аппроксимацией винеровского процесса с помощью случайного блуждания. [c.343]
Простейший метод дискретизации состоит в том, что после выбора А (скажем, 10 мин., 20 мин., 24 часа,. ..) вместо кусочно-цостоянного процесса 5 = (St)t o с непрерывным временем t 0 рассматривается новая последовательность 5Л = (Stk) с дискретным временем tk = kA, = 0,1,.... [c.393]