Теперь мы можем определить местоположение эффективного множества, применив теорему об эффективном множестве к достижимому множеству. Сначала выделим множество портфелей, удовлетворяющих первому условию теоремы об эффективном множестве. Если посмотреть на рис. 8.1, то можно заметить, что не существует менее рискового портфеля, чем портфель Е. Это объясняется тем, что если провести через Е вертикальную прямую, то ни одна точка достижимого множества не будет лежать левее данной прямой. При этом не существует более рискового портфеля, чем портфель Я. Это объясняется тем, что если провести через Н вертикальную линию, то ни одна точка достижимого множества не будет лежать правее данной прямой. Таким образом, множеством портфелей, обеспечивающих максимальную ожидаемую доходность при изменяющемся уровне риска, является часть верхней границы достижимого множества, расположенная между точками Е и Н. [c.196]
Рассматривая далее второе условие, можно заметить, что не существует портфеля, обеспечивающего большую ожидаемую доходность, чем портфель S, потому что ни одна из точек достижимого множества не лежит выше горизонтальной прямой, проходящей через S. Аналогично, не существует портфеля, обеспечивающего меньшую ожидаемую доходность, чем портфель G, потому что ни одна из точек достижимого множества не лежит ниже горизонтальной прямой, проходящей через G. Таким образом, множеством портфелей, обеспечивающих минимальный риск при изменяющемся уровне ожидаемой доходности, является часть левой границы достижимого множества, расположенная между точками S и G. [c.197]
Приложение Б показывает, как можно использовать рыночную модель для оценки ожидаемых доходностей, дисперсий и ковариаций ценных бумаг из достижимого множества. Имея данные оценки, можно последовательно определить эффективное множество. См. примечание 2. [c.229]
Как изменяется достижимое множество при введении в модель Марковица возможности получения и предоставления безрисковых займов Объясните словами и графически. [c.249]
На рис. 10.7 изображено достижимое множество модели Марковица, а также безрисковая ставка и соответствующее эффективное множество, представленное рыночной ли- [c.282]
Отношения (2.8) и (2.9) не являются связными, так как для произвольных векторных оценок w(a), w(b) часть неравенств (2.8) может выполняться "в одну сторону", (т. е. w.(a) > > w.(b)), а остальные — "в другую сторону" (го.(а) < го.(Ь)). Такие векторные оценки оказываются несравнимыми по Парето и образуют множество недоминируемых оценок, которым соответствует множество недоминируемых (эффективных по Парето) альтернатив. Таким образом, отличительной особенностью недоминируемых или эффективных по Парето альтернатив является то, что ни у одной из них ни по одному из их частных критериев оценка не может быть улучшена без ухудшения оценки какого-то другого (или других) критерия. Следовательно, эффективные альтернативы между собой несравнимы, и на множестве значений векторных оценок можно определить результат применения функции выбора. Этот результат применения функции выбора на множестве значений векторных оценок будем называть ядром отношения по заданной информации о предпочтениях ЛПР и обозначать eff(w,inf). Таким образом, ядро отношения Парето получит обозначение eff(w,iop). Для задач с положительно ориентированными критериями ядро eff(w,iop) отношения Парето расположено в северо-восточном направлении на границе достижимого множества векторных оценок. При этом мощность множества оценок ядра может быть различной в зависимости от конкретных особенностей (в частности, кон- [c.175]
| Рис. 136. Достижимое множество портфелей из п видов ценных бумаг |  |
| Рис. 4.3. Допустимое (достижимое) множество | 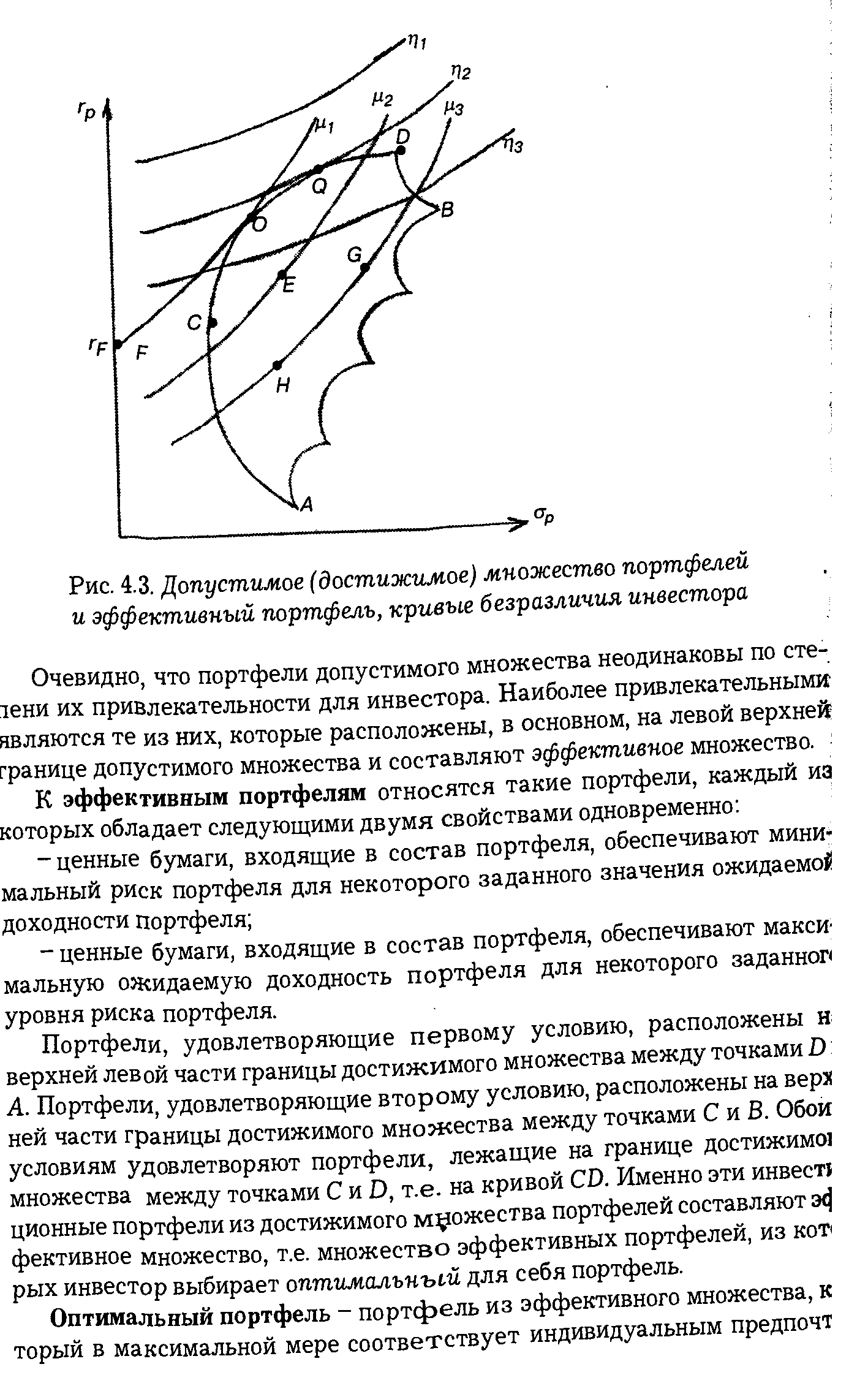 |
Множества достижимости 4Ь Модели агрегированные 47 [c.302]
Методы принятия решения при нескольких критериях превратились в самостоятельную область исследования совсем недавно, в семидесятых годах нашего века. Мы посвятим этим методам отдельный параграф гл. 6. Заранее отметим, что в качестве математического средства решения многокритериальных проблем используются методы оптимизации (в линейном случае — методы линейного программирования), а также некоторые другие методы (например, для построения множества достижимых значений показателей— методы теории линейных неравенств). [c.61]
Для анализа многокритериальной проблемы, поставленной здесь, можно попытаться построить множество эффективных значений показателей (если удастся сформулировать направления улучшения для всех показателей) либо построить множество всех достижимых значений показателей и представить его ЛПР для выбора наилучшего их сочетания (этот метод описан в 3 гл. 6). В качестве примера изображений, получаемых ЛПР па э.кране терминального устройства при анализе множества всех достижимых значений показателей 1)—7), рассмотрим рис. 3.1. На нем представлены G,, G2, G3 — три сечения множества достижимых значе- ний для модели (2.29) —(2.34) с по- Рис- 3.1. казателями (2.35) — (2.41). При этом [c.175]
Теперь рассмотрим некоторые характерные сечения множества достижимых значений показателей Л,..., Л (см. рис. 3.20— [c.231]
Общее поле поиска вариантов портфелей, из которых может быть выделено эффективное множество, определяемое термином допустимое (или достижимое) множество" [feasible set]. Оно характеризует всю совокупность вариантов портфелей, которые могут быть сформированы из конкретного числа рассматриваемых финансовых инструментов инвестирования. [c.354]
Рисунок 8.1 представляет иллюстрацию местоположения достижимого множества (feasible set), также известного как множество возможностей, из которого может быть выделено эффективное множество. Достижимое множество представляет собой все портфели, которые могут быть сформированы из группы в N ценных бумаг. Это означает, что все возможные портфели, которые могут быть сформированы из N ценных бумаг, лежат либо на границе, либо внутри достижимого множества (точки G, E, S и Н на рис. 8.1 являются примерами таких портфелей). В общем случае, данное множество будет иметь форму типа зонта, подобную изображенной на рисунке. В зависимости от используемых ценных бумаг, оно может быть больше смещено вправо или влево, вверх или вниз, кроме того, оно может быть шире или уже приведенного здесь множества. Главное, что, за исключением вырожденных случаев, оно будет похоже на множество, показанное на рис. 8.1. [c.196]
Effi ient Portfolio — эффективный портфель. Портфель, принадлежащий достижимому множеству и обеспечивающий инвестору как максимальную ожидаемую доходность при заданном уровне риска, так и минимальный риск при заданном значении ожидаемой доходности. [c.972]
Feasible Set (или Opportunity Set) - достижимое множество. Множество портфелей, которые можно сформировать из ценных бумаг, рассматриваемых инвестором. [c.975]
Методы второй группы направлены на.то, чтобы дать человеку представление об эффективном множестве в целом. Далее, человек может сам выбрать то эффективное решение, которое устраивает его в наибольшей степени. Надо сказать, что в том случае, когда число показателей превышает два, эта задача является весьма сложной. Она усугубляется тем, что даже для линейных задач множество эффективных точек является певыпуклым. Для систем с выпуклыми множествами допустимых решений п линейными показателями эту трудность можно преодолеть, если дать представление о всем множестве достижимых значений показателей. В указанном случае это множество является выпуклым, поэтому его структуру можно понять па основе анализа различных двумерных сечений этого множества. Заметим, что при этом одновременно дается представление о структуре эффективного множества, которое является частью границы множества достижимых показателей. [c.61]
Указанный недостаток оптимизации носит технический характер и преодолевается с разработкой новых, более эффективных методов оптимизации и с повышением мощности ЭВМ. Более принципиальное значение имеет другой недостаток оптимизации — необходимость построения единственного критерия оптимизации. Оказалось, что в большинстве задач заказчик не может сформулировать такой критерий и соизмерить тем самым различные показатели. Искусственное объединение различных показателей в один часто приводило к тому, что заказчик отказывал- ся использовать решение, найденное с помощью математических моделей и такого критерия. Для преодоления подобных трудностей наряду с имитационными методами, для которых многокри-териальность помехой не является, стали разрабатываться многокритериальные методы. Основными понятиями многокритериальных методов (см. 4 гл. 1) являются понятия множества всех достижимых значений показателей и множества их эффективных значений. Пусть для модели народного хозяйства выбраны два [c.151]
Для исследования описанной модели было построено множество достижимых значений показателей в семимерном пространстве /1, /з,. .., /7 . На основе достаточного числа (около сотни) [c.230]
