Первый член описывает обычно минимизируемое в методе обратного распространения ошибки квадратичное отклонение выхода нейронной сети у = y(x,w) n желаемого значения yd. Второе слагаемое представляет собой квадратичное отклонение исправленного входного [c.177]
При проектировании архитектуры нейронной сети необходимо определить число слоев нейронов и количество нейронов в каждом слое. Процедура обратного распространения применима к сетям с любым числом слоев, но традиционно рассматриваются сети, содержащие входной, выходной и скрытый слой. Число нейронов в выходном и входном слоях определяется соответственно количеством выходов и входов системы. В общем случае, чем меньше нейронов в выходном слое, тем быстрее сеть обучается. [c.126]
Методы построения и обучения нейронной сети к настоящему времени достаточно хорошо разработаны и базируются на широко известном алгоритме обратного распространения ошибки [29]. В процессе анализа обучающей выборки нейронная сеть с предварительно заданной избыточной структурой выполняет следующие процедуры (рис.2. И) . [c.158]
Анализ (в смысле. математический или комплексный анализ) является расширением классического исчисления. Аналитические оптимизаторы используют наработанные методы, в особенности методы дифференциального исчисления и исследования аналитических функций для решения практических задач. В некоторых случаях анализ дает прямой (без перебора вариантов) ответ на задачу оптимизации. Так происходит при использовании множественной регрессии, где решение находится с помощью нескольких матричных вычислений. Целью множественной регрессии является подбор таких весов регрессии, при которых минимизируется сумма квадратов ошибок. В других случаях требуется перебор вариантов, например невозможно определить напрямую веса связей в нейронной сети, их требуется оценивать при помощи алгоритма обратного распространения. [c.57]
Тем не менее низкая скорость оптимизации не является главным препятствием на пути аналитика. Гораздо сложнее справиться с так называемой проблемой локальных решений. Почти все аналитические методы, будь они простыми или сложными, легко попадаются в ловушку локальных максимумов при наличии множества впадин и выступов на поверхности они не могут найти наилучшее глобальное решение. Метод наименьших квадратов, моделирование нейронными сетями дают поверхности функции пригодности неправильной формы с большим количеством локальных экстремумов. Данные поверхности чрезвычайно сложны для стандартных аналитических методов, таких как метод сопряженных градиентов или алгоритм обратного распространения, применяемый в нейронных сетях. Впрочем, местные максимумы можно обойти, соединив аналитический метод с генетическим. Для поверхностей, которые можно исследовать аналитическими методами, такой двойной алгоритм может оказаться наилучшим решением он позволит быстро и с большой точностью найти глобальные оптимумы. [c.58]
| Рисунок 0.1. Нейронная сеть, обучаемая с учителем при помощи метода обратного распространения ошибки, в сравнении с самоорганизующейся картой. | 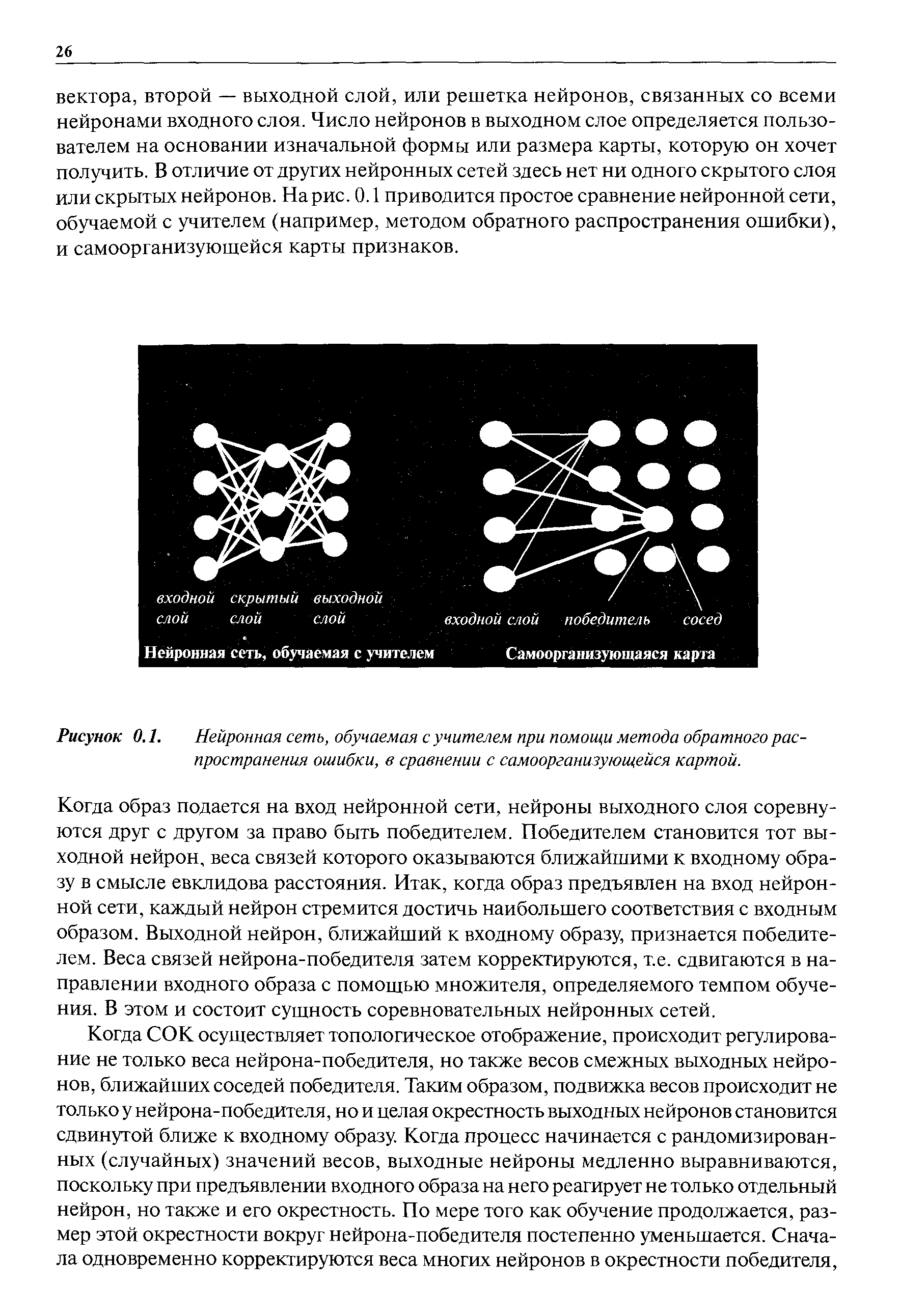 |
Сеть с обратным распространением состоит из одного уровня входящих данных, одного или нескольких скрытых уровней и одного уровня выходных данных. Уровень входящих данных состоит из нейрона, связанного с каждой входящей независимой переменной. Уровень выходных данных содержит нейрон, относящийся к каждой зависимой переменной, которую надо спрогнозировать. Скрытый уровень состоит из нейронов, которые связаны как с входящими, так и с выходящими данными. Как правило, уровни имеют полные связи между собой. Это означает, что каждый нейрон на каждом уровне связан с каждым из нейронов соседнего уровня. [c.130]
Наиболее распространенным алгоритмом обучения нейронной сети является алгоритм обратного распространения ошибки. Целевая функция по этому алгоритму должна обеспечить минимизацию квадрата ошибки в обучении по всем примерам [c.31]
Для обучения сети используются различные алгоритмы обучения и их модификации [9, И, 22, 42, 70, 139]. Очень трудно определить, какой обучающий алгоритм будет самым быстрым при решении той или иной задачи. Наибольший интерес для нас представляет алгоритм обратного распространения ошибки, так как является эффективным средством для обучения многослойных нейронных сетей прямого распространения [85, 127]. Алгоритм минимизирует среднеквадратичную ошибку нейронной сети. Для этого с целью настройки синаптических связей используется метод градиентного спуска в пространстве весовых коэффициентов и порогов нейронной сети. Следует отметить, что для настройки синаптических связей сети используется не только метод градиентного спуска, но и методы сопряженных градиентов, Ньютона, квазиньютоновский метод [94]. Для ускорения процедуры обучения вместо постоянного шага обучения предложено использовать адаптивный шаг обучения a(t). Алгоритм с адаптивным шагом обучения работает в 4 раза быстрее. На каждом этапе обучения сети он выбирается таким, чтобы минимизировать среднеквадратическую ошибку сети [29, 36]. [c.65]
Сети обратного распространения (Ba k Propagation Network) — многоуровневая нейросеть, в которой ошибки отсылаются на обработку с целью уравновесить значимость нейронов. [c.365]
Дальнейшее развитие многослойных сетей долгое время сдерживалось отсутствием теоретически обоснованного алгоритма обучения, причем было неясно, возможно ли это вообще. Однако оказалось, что оценки Минского слишком пессимистичны. В 1986 г. Д. Руммельхарт в соавторстве опубликовал полное и ясное теоретическое обоснование процедуры обучения многослойной нейронной сети, названного авторами методом обратного распространения ошибки (ba kpropagation). Любопытно, что как только статья была опубликована, выяснилось, что предлагаемый метод обучения был предвосхищен Д. Паркером в 1982 г. И вскоре выяснилось, что еще раньше, в 1974 г., этот метод был описан в статье П. Вербу. [c.131]
Дело в том, что ошибка сети определяется по ее выходам, т.е. непосредственно связаня лишь с выходным слоем весов. Вопрос состоял в том, как определить ошибку для нейронов на скрытых слоях, чтобы найти производные по соответствующим весам. Нужна была процедура передачи ошибки с выходного слоя к предшествующим слоям сети, в направлении обратном обработке входной информации. Поэтому такой метод, когда он был найден, получил название метода обратного распространения ошибки. [c.58]
Существует два основных подхода к управлению темпом обучения персептрона методом обратного распространения ошибки. При первом этот темп одновременно и равномерно уменьшается для всех нейронов сети в зависимости от одного глобального критерия -достигнутой среднеквадратичной погрешности на выходном слое. При этом сеть быстро учится на начальном этапе обучения и избегает осцилляции ошибки на позднем. Во втором случае оцениваются изменения отдельных межнейронных связей. Если на двух последующих шагах обучения инкременты связей имеют противоположный знак, то разумно уменьшить соответствующий локальный темп - впротивном случае его следует увеличить. Использование нечетких правил может обеспечить более аккуратное управление локальными темпами модификации связей. В частности это может быть достигнуто, если в качестве входных параметров этих правил использовать последовательные значения градиентов ошибки. Таблица соответствующих правил может иметь, например следующий вид [c.208]
Рассмотрим теперь наиболее распространенный алгоритм обучения нейронных сетей с прямой связью — алгоритм обратного распространения ошибки (Ba kpropagation, BP), представляющий собой развитие так называемого обобщенного дельта-правила (см. [281]). Этот алгоритм был заново открыт и популяризирован в 1986 г. Ру-мельхартом и МакКлеландом из знаменитой Группы по изучению параллельных распределенных процессов в Массачусетском технологическом институте. В этом пункте мы более подробно рассмотрим математическую суть алгоритма. Он является алгоритмом градиентного спуска, минимизирующим суммарную квадратичную ошибку [c.28]
Нейронные сети с прямой связью и обучением методом обратного распространения ошибки рассматриваются в литературе чаще других. Кроме них, существует много других сетевых моделей, некоторые из которых имеют вычурные названия конкурентное обучение (или адаптивная теория резонанса ), сети Хопфилда, машины Больцмана, самоорганизующиеся карты признаков Кохонена. [c.36]
Представляется, что нейронные сети лучше, чем другие методы, подходят для выявления нелинейных закономерностей в отсутствие априорных знаний об основной модели. Их можно применять во всех случаях, где обычно используются линейные (или преобразованные линейные) методы с проведением оценок посредством подходящего статистического метода (см. [114]). Чтобы лучше представить себе возможности нейронных сетей, рассмотрим процесс обучения очень простой многослойной сети с алгоритмом обратного распространения ошибки (MBPN) на искусственно смоделированном псевдохаотическом временном ряде. Начнем с простого логистического механизма обратной связи, описанного выше (см. рис. 3.4) [c.80]
Обучение нейронной сети обычно рассматривается как решение оптимизационной задачи минимизация функции ошибки или невязки на данном множестве примеров путем выбора значений весов ay. Разработано очень много обучающих алгоритмов, отличающихся друг от друга стратегией оптимизации и критерием ошибки (функцией). Выбор алгоритма обучения также зависит от знаний и опыта специалиста. Наиболее распространенным алгоритмом обучения нейронных сетей с прямой связью является алгоритм обратного распространения ошибки (Ba kpropagation - ВР). На этапе проверки достоверности работа сети сравнивается с данными контрольного множества. Желательно, чтобы они полностью отличались от применявшихся на предыдущем этапе. [c.279]
Существуют различные алгоритмы обучения нейронных сетей, одним из наиболее популярных является алгоритм обратного распространения ошибки (Ba kpropagation, BP), в современном виде разработанный в Массачусетском технологическом институте и являющийся по существу методом градиентного спуска. [c.144]
Перед использованием нейронной сети производится ее обучение, что представляет собой итерационный процесс настройки весовых коэффициентов. Для обучения применяются специальные алгоритмы. Наибольшее распространение получили градиентные методы обучения - алгоритм обратного распространения ошибки (Ba k Propagation), сопряженных градиентов, RProp и другие. Для проверки адекватности построенной нейронной сети используется специальный прием - тестовое подтверждение. [c.17]
Программный пакет SAS Neural Network Appli ation предназначен для обучения множества разновидностей нейронных сетей и включает в себя графический интерфейс пользователя. Данный пакет предусматривает возможность обучения на месте и настраивается с учетом потребностей пользователя. Основные функции пакета включают в себя многослойные перцептроны, сети радиального базиса, статистические версии обратного распространения ошибки и дискретизации обучаемого вектора, множество встроенных функций активации и ошибок, множественные скрытые слои, прямые связи между входами и выходами, обработку ситуаций с пропущенными данными, категориальные переменные, стандартизацию входных данных и целей и предварительную оптимизацию с помощью случайных начальных данных с целью избежать попадания в локальные минимумы. Обучение осуществляется с использованием стандартных численных алгоритмов оптимизации вместо более трудоемкого метода обратного распространения ошибки. [c.260]
Обратное распространение (Ba kpropagation). Метод обучения, при котором многослойная нейронная сеть с прямыми связями применяется для распознавания образов или классификации с учителем и передачей (или распространением) по обратной связи информации об ошибке. [c.310]
Используемые в системе "Forex-94" нейронные сети прогнозируют решения о покупке/продаже валюты на основе их обучения по изменениям курсов валют за определенные периоды времени. Тогда прогноз сводится к сопоставлению произошедших изменений курсов валют с изменениями за эквивалентный период времени, "запомненными" в нейронной сети, по которым происходит активация решающей прогнозной функции (нейрона). В процессе обучения нейронная сеть использует алгоритм обратного распространения ошибок, который позволяет свести их к заданным интервалам погрешности. В качестве исходной информации для прогноза нейронная сеть может использовать не только конкретные значения валютных курсов, но и сигналы методов технического анализа. Вместе с тем, нейронные сети "Forex-94" позволяют прогнозировать не сам валютный курс, а лишь его скользящее среднее за заданный интервал времени. [c.117]
