Нейронные сети с прямой связью состоят из статических нейронов, так что сигнал на выходе сети появляется в тот же момент, когда подаются сигналы на вход. Организация (топология) сети может быть различной. Если не все составляющие ее нейроны являются выходными, говорят, что сеть содержит скрытые нейроны. Наиболее общий тип архитектуры сети получается в случае, когда все нейроны связаны друг с другом (но без обратных связей). В конкретных задачах нейроны обычно бывают сгруппированы в слои. На рис. 1.3 показана типовая схема нейронной сети с прямой связью с одним скрытым слоем. [c.23]
| Рис. 1.3. Нейронная сеть с прямой связью с одним скрытым слоем (пороги не отмечены) | 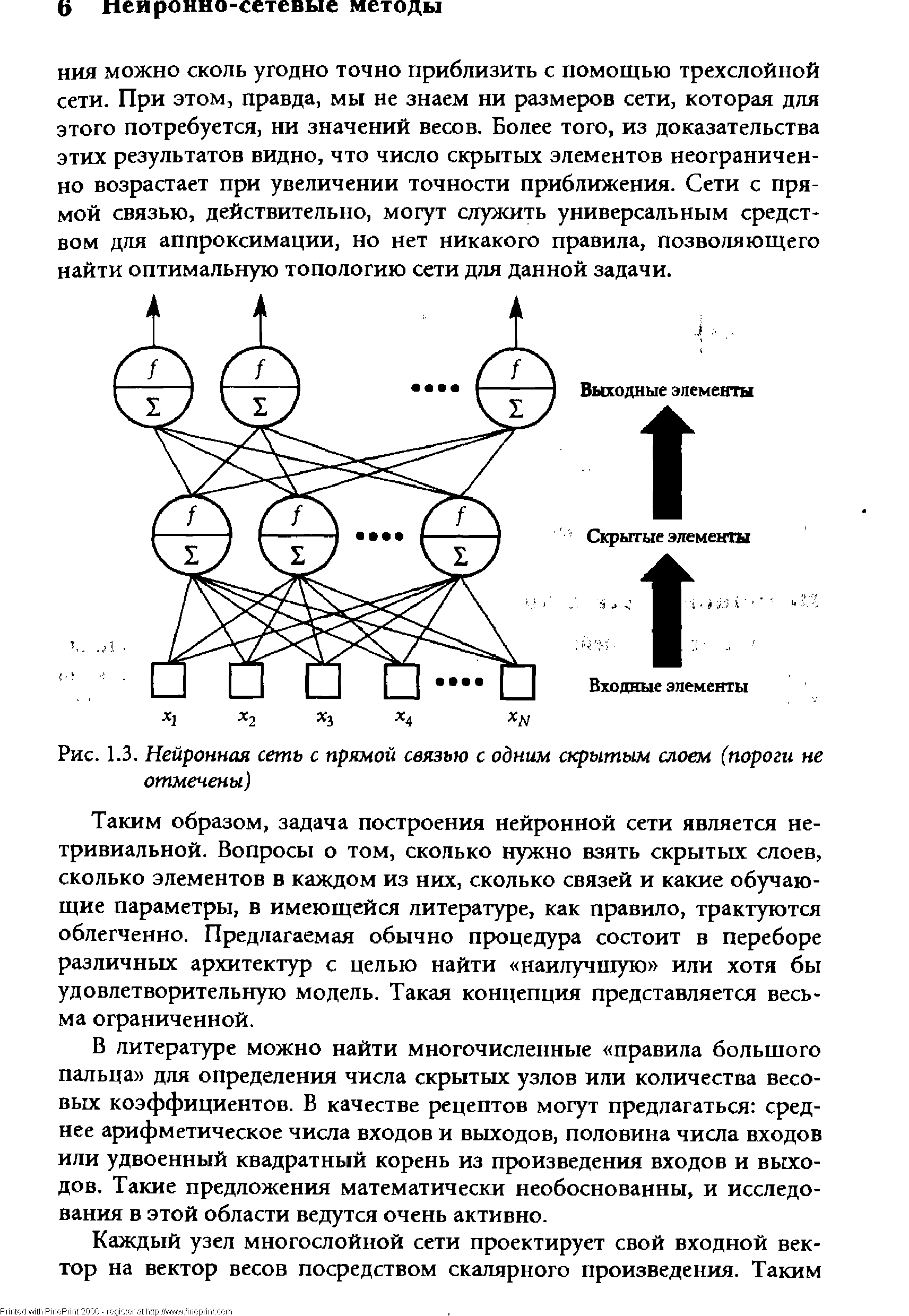 |
В предыдущей главе мы рассмотрели методы нейронных вычислений. В настоящей главе мы исследуем две главные области применения сетей с прямой связью задачи классификации и моделирование временных рядов. Отличие между задачами этих двух типов состоит в наличии (временной) упорядоченности примеров. [c.42]
Нейронная сеть с прямой связью как классификатор [c.46]
Богатые возможности отображения особенно важны в тех случаях, когда на основе нескольких оценок строится высокоуровневая процедура принятия решений. Известно много приложений нейронных сетей с прямой связью к задачам классификации. Как правило, они оказываются эффективнее других методов, потому что нейронная сеть генерирует бесконечное число нелинейных регрессионных моделей (см. [230]). [c.46]
Модели, основанные на нейронных сетях с прямой связью [c.56]
Анализ (в смысле. математический или комплексный анализ) является расширением классического исчисления. Аналитические оптимизаторы используют наработанные методы, в особенности методы дифференциального исчисления и исследования аналитических функций для решения практических задач. В некоторых случаях анализ дает прямой (без перебора вариантов) ответ на задачу оптимизации. Так происходит при использовании множественной регрессии, где решение находится с помощью нескольких матричных вычислений. Целью множественной регрессии является подбор таких весов регрессии, при которых минимизируется сумма квадратов ошибок. В других случаях требуется перебор вариантов, например невозможно определить напрямую веса связей в нейронной сети, их требуется оценивать при помощи алгоритма обратного распространения. [c.57]
До сих пор речь шла о сетях, в которых сигналы распространялись в прямом направлении, т. е. они не имели обратных связей. Такие сети всегда устойчивы. Если в нейронной сети завести сигналы с выхода на вход т. е. ввести обратные связи, это приводит к переходным процессам, после которых сеть может прийти в некоторое устойчивое состояние. Однако возможно и такое, что в сети никогда не наступит состояние равновесия, т. е. она будет неустойчивой. Анализ устойчивости нейросетей с обратными связями — сложная задача. Однако существуют нейросети с обратными связями, устойчивость которых при определенных условиях может быть доказана. К таким сетям относится сеть Хопфилда. Это простая сеть из одного слоя нейронов с обратными связями. Сеть Хопфилда можно рассматривать как примитивную модель ассоциативной памяти, позволяющую по некоторому входному образу извлечь ближайший к нему эталон. Для этого сеть надо предварительно обучить по некоторой обучающей выборке. Но учителя при этом не потребуется, то есть не будет производится сопоставление входного и выходного образов. Сети предъявляют серию входных образов, и они запоминаются в синаптической карте, которая формируется с помощью формулы [c.133]
Искусственная нейронная сеть построена из нейронов, связанных друг с другом. Даже если работа нейронной сети имитируется на компьютере, лучше представлять ее себе не как программу, а как электронную схему. Мы будем рассматривать два вида нейронных сетей статические, которые также часто называют сетями с прямой связью (feed-forward), и динамические, или рекуррентные сети. В этом разделе мы займемся статическими сетями. Сети других видов будут кратко рассмотрены позднее. [c.23]
Интересно отметить, что, согласно теоретическим результатам [79], [ 118], нейронные сети с прямой связью и с сигмоидными функциями являются универсальным средством для приближения (аппроксимации) функций. Говоря точнее, любую вещественнозначную функцию нескольких переменных на компактной области определе- [c.23]
Рассмотрим теперь наиболее распространенный алгоритм обучения нейронных сетей с прямой связью — алгоритм обратного распространения ошибки (Ba kpropagation, BP), представляющий собой развитие так называемого обобщенного дельта-правила (см. [281]). Этот алгоритм был заново открыт и популяризирован в 1986 г. Ру-мельхартом и МакКлеландом из знаменитой Группы по изучению параллельных распределенных процессов в Массачусетском технологическом институте. В этом пункте мы более подробно рассмотрим математическую суть алгоритма. Он является алгоритмом градиентного спуска, минимизирующим суммарную квадратичную ошибку [c.28]
Нейронные сети с прямой связью и обучением методом обратного распространения ошибки рассматриваются в литературе чаще других. Кроме них, существует много других сетевых моделей, некоторые из которых имеют вычурные названия конкурентное обучение (или адаптивная теория резонанса ), сети Хопфилда, машины Больцмана, самоорганизующиеся карты признаков Кохонена. [c.36]
Рассмотрим, как нейронные сети с прямой связью (или многослойные персептроны — MLP, Multilayer Per eptron) используются в задачах классификации. В чем, собственно, заключается эта задача Во-первых, в любой задаче классификации требуется отнести имеющиеся статические образцы (рукописные буквы, звуковые сигналы, характеристики финансового положения) к определенным классам. Разнообразие примеров, возникающих в реальном мире, практически бесконечно. Эффективность классификации зависит от способа представления этих форм. В числе других здесь имеются следующие способы распознавание образов, структурное представление и ста- [c.42]
К сожалению, хотя теоретически характеристики нейронной сети с прямой связью стремятся к байесовской, в применении их к практическим задачам выявляется ряд недостатков. Во-первых, заранее неизвестно, какой сложности (т.е. размера) сеть потребуется для достаточно точной реализации отображения. Эта сложность может оказаться чрезмерно большой. Архитектура сети, т.е. число слоев и число элементов в каждом слое, должна быть зафиксирована до начала обучения. Эта архитектура порождает сложные нелинейные разделяющие поверхности в пространстве входов. В сети с одним скрытым слоем векторы образцов сначала преобразуются (нелинейным образом) в новое пространство представлений (пространство скрытого слоя), а затем гиперплоскости, соответствующие выходным узлам, располагаются так, чтобы разделить классы уже в этом новом пространстве. Тем самым, сеть распознает уже другие характерис- [c.46]
Настройка классификатора обычно бывает основана на пороговых правилах и/или сравнении расстояний между значениями целевых показателей. Нужно помнить, что нейронная сеть с прямой связью и сигмоидными выходами выдает ответ в непрерывном виде, обычно в интервале от 0 до 1 в зависимости от того, как располагаются разделяющие гиперплоскости скрытых элементов. Однако, даже если на выходе используются не апостериорные вероятности, а какая-либо более простая решающая функция, имеется возможность выдать надежный ответ. Настраивая критерий отбрасывания, можно [c.51]
Простая нейронная сеть с прямой связью в форме электронной таблицы с пятью скрытыми элементами для задачи Фишера об ирисах (Прим. ред. Общий вид диалогового окна программы-макроса >v в системе Ex et) [c.70]
Обучение нейронной сети обычно рассматривается как решение оптимизационной задачи минимизация функции ошибки или невязки на данном множестве примеров путем выбора значений весов ay. Разработано очень много обучающих алгоритмов, отличающихся друг от друга стратегией оптимизации и критерием ошибки (функцией). Выбор алгоритма обучения также зависит от знаний и опыта специалиста. Наиболее распространенным алгоритмом обучения нейронных сетей с прямой связью является алгоритм обратного распространения ошибки (Ba kpropagation - ВР). На этапе проверки достоверности работа сети сравнивается с данными контрольного множества. Желательно, чтобы они полностью отличались от применявшихся на предыдущем этапе. [c.279]
Существует большое разнообразие нейронных сетей, отличающихся своей архитектурой , т.е. способом связи виртуальных нейронов, деталями их поведения (обработкой сигнала или функциями передачи ) и процессом обучения. Существуют различные виды архитектур сетей представляющих интерес для трейдеров, например сети Коонена и сети с квантованием обучающего вектора (LVQ), различные сети с адаптивным резонансом и периодические сети. В этой главе будет рассмотрена наиболее популярная и полезная во многих отношениях архитектура, а именно нейронная сеть с прямой связью. [c.253]
Сеть с прямой связью состоит из слоев нейронов. Первый слой, входной, получает информацию или вводы извне. Этот слой состоит из независи- [c.253]
Обратное распространение (Ba kpropagation). Метод обучения, при котором многослойная нейронная сеть с прямыми связями применяется для распознавания образов или классификации с учителем и передачей (или распространением) по обратной связи информации об ошибке. [c.310]
Для обучения сети используются различные алгоритмы обучения и их модификации [9, И, 22, 42, 70, 139]. Очень трудно определить, какой обучающий алгоритм будет самым быстрым при решении той или иной задачи. Наибольший интерес для нас представляет алгоритм обратного распространения ошибки, так как является эффективным средством для обучения многослойных нейронных сетей прямого распространения [85, 127]. Алгоритм минимизирует среднеквадратичную ошибку нейронной сети. Для этого с целью настройки синаптических связей используется метод градиентного спуска в пространстве весовых коэффициентов и порогов нейронной сети. Следует отметить, что для настройки синаптических связей сети используется не только метод градиентного спуска, но и методы сопряженных градиентов, Ньютона, квазиньютоновский метод [94]. Для ускорения процедуры обучения вместо постоянного шага обучения предложено использовать адаптивный шаг обучения a(t). Алгоритм с адаптивным шагом обучения работает в 4 раза быстрее. На каждом этапе обучения сети он выбирается таким, чтобы минимизировать среднеквадратическую ошибку сети [29, 36]. [c.65]
Программный пакет SAS Neural Network Appli ation предназначен для обучения множества разновидностей нейронных сетей и включает в себя графический интерфейс пользователя. Данный пакет предусматривает возможность обучения на месте и настраивается с учетом потребностей пользователя. Основные функции пакета включают в себя многослойные перцептроны, сети радиального базиса, статистические версии обратного распространения ошибки и дискретизации обучаемого вектора, множество встроенных функций активации и ошибок, множественные скрытые слои, прямые связи между входами и выходами, обработку ситуаций с пропущенными данными, категориальные переменные, стандартизацию входных данных и целей и предварительную оптимизацию с помощью случайных начальных данных с целью избежать попадания в локальные минимумы. Обучение осуществляется с использованием стандартных численных алгоритмов оптимизации вместо более трудоемкого метода обратного распространения ошибки. [c.260]
