В задаче о максимальном потоке мощность источника v, равная потреблению в пункте потребления, не считается заданной. Наоборот, в задачах такого типа требуется максимизировать величину v исходя из возможностей транспортной сети, передать все произведенное количество груза потребителю. [c.162]
Задача о максимальном потоке может быть поставлена и в более сложном виде. Например, часто накладываются ограничения на пропускные способности узлов. [c.163]
Задача о максимальном потоке. Теперь рассмотрим один важ ный случай линейной задачи на сети — так называемую задачу о максимальном потоке. Пусть в транспортной сети есть всего один пункт производства и единственный пункт потребления, соединенные между собой транспортной сетью, проходящей через [c.188]
В задаче о максимальном потоке мощность источника г , равная спросу в пункте потребления, не считается заданной. Наоборот, в задачах такого типа требуется максимизировать величину у для заданной транспортной сети. [c.188]
Задача о максимальном потоке 188 [c.391]
Задача о максимальном потоке. Как (по каким маршрутам) послать максимально возможное количество грузов из начального пункта в конечный, если пропускная способность путей между пунктами ограничена [c.180]
Решение задачи о максимальном потоке может быть получено из следующих соображений. [c.180]
| Рис. 1.25. Исходные данные к задаче о максимальном потоке | 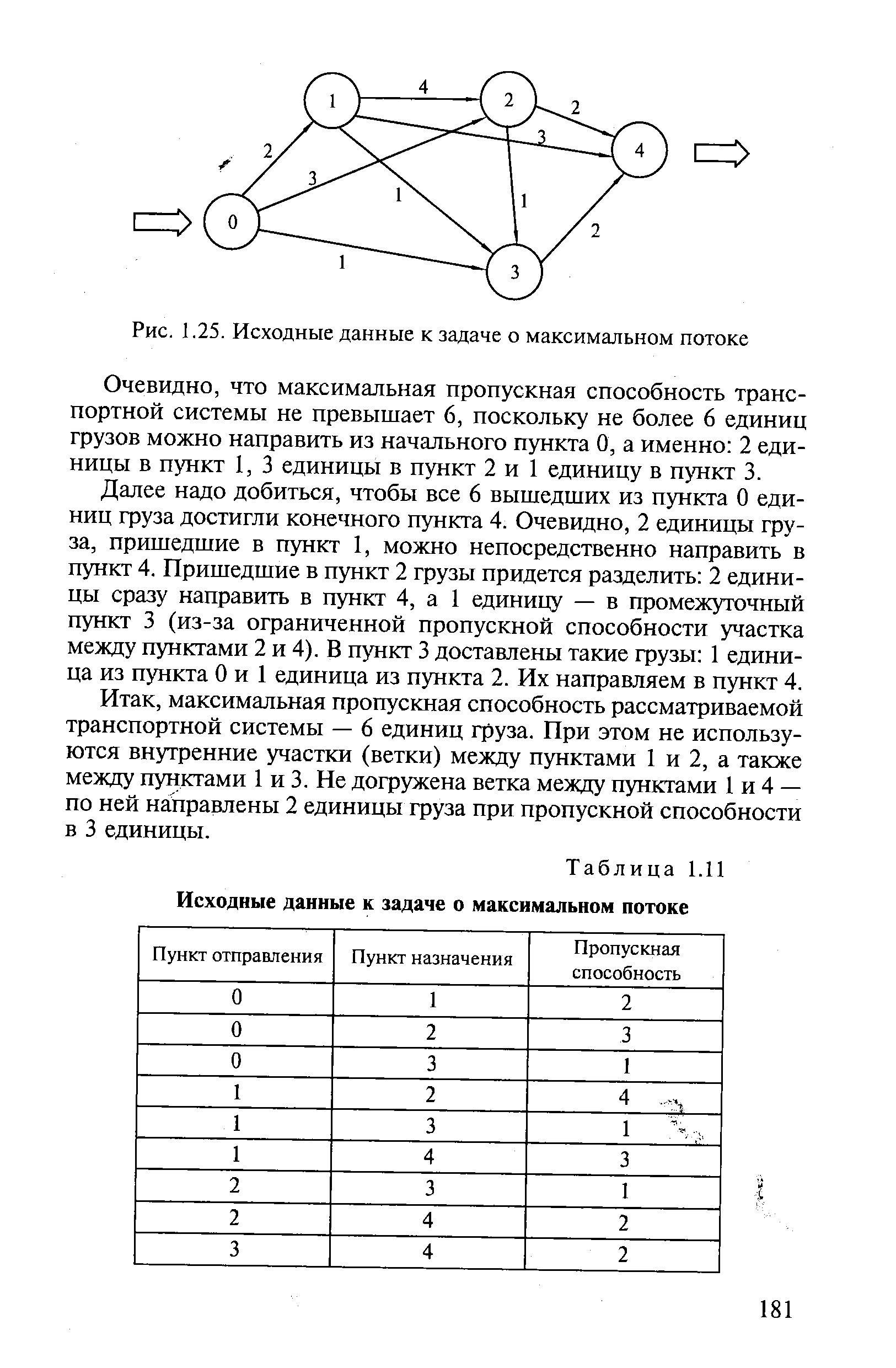 |
| Таблица 1.12 Решение задачи о максимальном потоке | 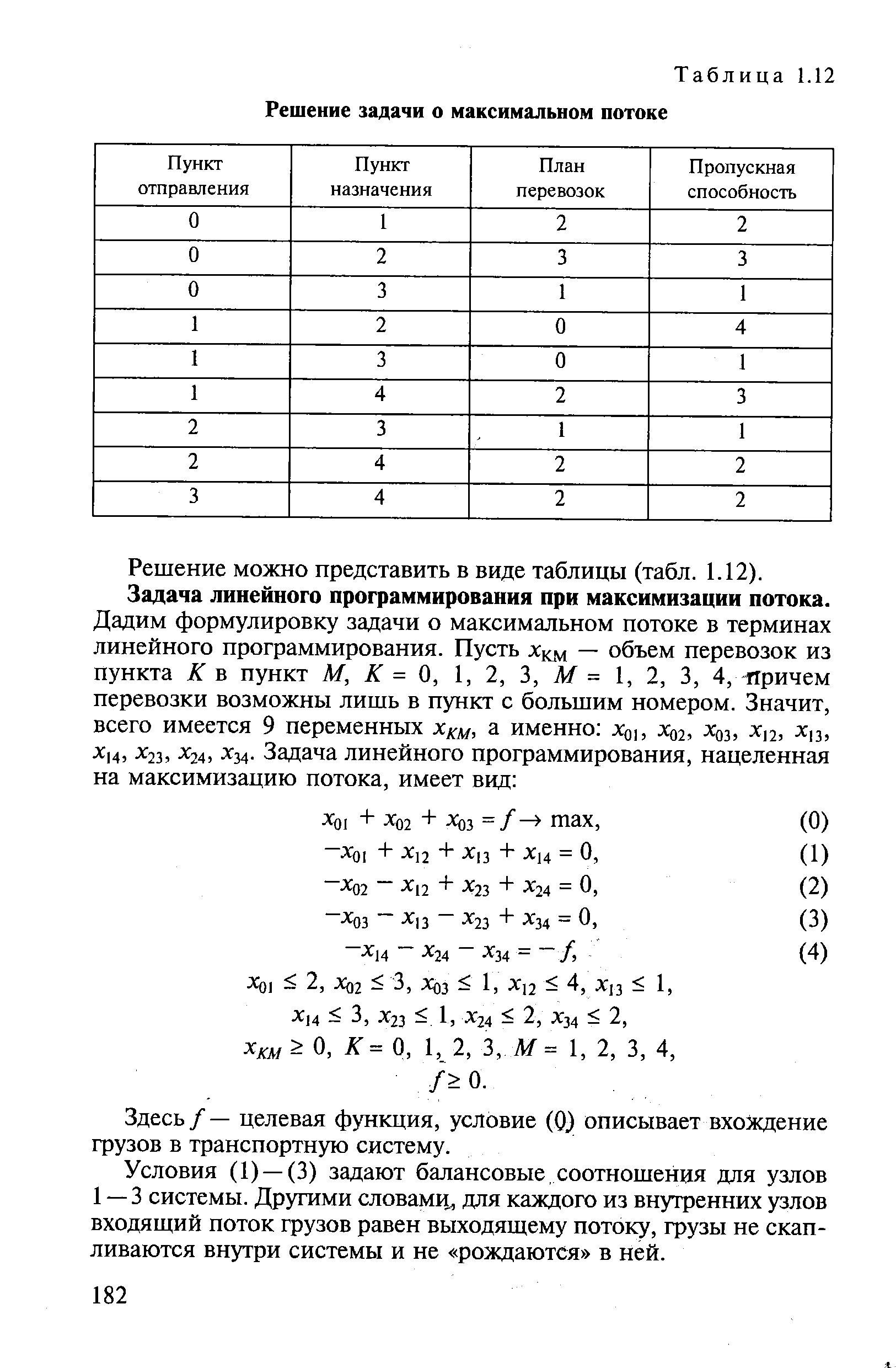 |
Применительно к рассматриваемой системе будем решать задачу о максимальной средней мощности р, которой эквивалентна постановка о максимальной интенсивности теплового потока при средней интенсивности изменения энтропии рабочего тела, равной нулю. Оптималь- [c.79]
При ограничении на продолжительность процесса задача о максимальной работе сводится к задаче оптимального управления, особенности которой во многих практически важных случаях делают структуру оптимального решения независимой от уравнений состояния подсистем и кинетики потоков, причем минимальная работа разделения равновесной системы на подсистемы при фиксированной продолжительности однозначно определяется через максимальную работу в прямом процессе и обратимую работу разделения. [c.108]
Векторные потоки сырья и готовой продукции. Приведем постановку задачи о максимальной прибыли для случая, когда предприятие производит п видов продукции, продаваемых на рынке по ценам pui в количестве 2г(рпО> г — 1 -j j и закупает m видов сырья по ценам p k в количестве gik(p k)i k = 1,. . . , m. При этом для производства единицы продукции г -го вида требуется аа-/. единиц сырья k-ro вида. Задача примет вид [c.291]
Сортность и качество нефтепродуктов, необходимых нефтебазам для обеспечения тяготеющих IK ним потребителей, диктуют номенклатуру производства этих нефтепродуктов на НПЗ. В связи с тем, что нефтепродукты на НПЗ по временам года производятся относительно равномерно, а реализация их через нефтебазы неравномерна, для максимального использования мощностей как действующих, так и проектируемых НПЗ следует правильно решить вопрос о размещении емкостей межсезонных запасов нефтепродуктов (на каждой нефтебазе или на отдельных нефтебазах с большим грузооборотом). При равномерном производстве на НПЗ в осенне-зимний период образуются излишки светлых нефтепродуктов, а в весенне-летнее время нехватка их. Поэтому вопрос определения объема и размещения резервуарной емкости. межсезонного хранения (МСХ) нефтепродуктов, накапливаемых в осенне-зимний и расходуемых в весенне-летний периоды, имеет большое народнохозяйственное значение. Расчеты показали, что размещение емкости МСХ нефтепродуктов на отдельных крупных нефтебазах выгоднее, чем размещение ее на каждой нефтебазе. Для решения экономико-математической задачи выбора МСХ нефтепродуктов предложен эвристический метод, базирующийся на многократном нахождении максимального потока в сети специальной структуры, в сочетании с методом случайного поиска, а также точный метод — решение сетевой параметрической задачи. [c.41]
В термодинамике при конечном времени решают задачи о максимуме извлеченной работы для систем, как содержащих, так и не содержащих резервуара, при ограниченной продолжительности процесса или при заданной интенсивности потоков. Максимальную работу (работоспособность), найденную при этих ограничениях, будем обозначать через LT или Lp соответственно. [c.70]
Задачу (8.89) нужно решать одновременно с вычислением максимального потока п (р) прибыли фирмы. Будем предполагать, что каждый из потоков gj( j,pj) монотонно зависит от су, знак потока положителен, если он направлен от подсистемы к фирме (закупки) и отрицателен при продаже. В этом случае мы можем выразить цену закупки (продажи) j(gj,pj) у j-ro ЭА через величину потока и записать задачу о максимуме прибыли как [c.305]
Если объединить поставленные задачи развития экономических отношений нового порядка в России для выработки единого курса действий, то речь будет идти о необходимости восстановления нарушенного баланса потоков между основными секторами экономики на фоне сбалансированно развитых общественных отношений в государстве, обеспечивающих максимальное удовлетворение личных и общественных интересов. Для решения этой задачи могут быть использованы различные подходы и методики, которые позволяют квалифицированно подойти к процессу формирования наиболее действенной программы по созданию относительно устойчивых условий существования экономических систем. Речь идет о формировании и реализации многоуровневой антикризисной программы, предполагающей [c.5]
Одна из общих задач логистики заключается также в создании интегрированной эффективной системы регулирования и контроля материальных и информационных потоков, обеспечивающей высокое качество поставки продукции. С ней самым тесным образом сопряжено решение таких проблем, как соответствие друг другу материальных и информационных потоков, контролирование материального потока и передача данных о нем в единый центр, определение стратегии и технологии физического перемещения товаров, разработка способов управления операциями движения товаров, установление норм стандартизации полуфабрикатов и упаковки, определение объема производства, транспортировки и складирования, расхождение между желаниями и возможностями закупки и производства. Примером частной задачи логистики может служить создание минимальных производственных запасов и максимальное сокращение времени хранения и транспортировки грузов. [c.33]
Таким образом, в каждый момент времени инвестор может вычислить (на основе сложившихся в этот момент цен и прогнозов будущих денежных потоков) ожидаемый чистый приведенный доход от созданной им фирмы. Задача инвестора состоит в том, чтобы на основе информации о наблюдаемых в каждый момент времени ценах выбрать момент инвестирования таким образом, чтобы этот доход был максимальным. Правило, согласно которому выбирается момент инвестирования, и определяет поведение инвестора. [c.10]
Чтобы ускорить получение денег, нужно максимально облегчить кредитору его задачу -принятие решения о предоставлении кредита При первой же встрече с кредитором ваши сотрудники должны предоставить ему прогноз денежного потока компании и план потребности в денежных средствах и иных активах Это поможет кредитору решить, являетесь ли вы для него подходящим клиентом или нет [c.167]
Менеджеры фирмы. Формально их задачей является принятие решений по текущему управлению финансами фирмы, т. е. задача менеджеров предельно проста -нужно так организовать вверенные им для управления ресурсы, чтобы собственники фирмы получили наибольший эффект. Эти решения касаются текущего управления денежными потоками, а также осуществления плановых инвестиций в пределах компетенции. Сказанное относительно задач, стоящих перед менеджерами, в современной бизнес-среде имеет скорее теоретическое, нежели реально-фактическое значение. Дело в том, что в крупном бизнесе имеет место своеобразное перераспределение функций и полномочий в отношении реального управления активами фирмы, результатом которого является исключительно значимая роль топ-менеджеров, становящихся, если можно так сказать, неформальными собственниками фирмы. С течением времени возможно проявление тенденции, когда топ-менеджеры не ограничиваются исполнением своих функций исходя исключительно из приоритетности интересов собственников, а помимо этого принимают во внимание и собственные интересы. При этом они выступают в роли как потребителей информации, так и ее производителей , источников. Имеется в виду, что менеджеры, с одной стороны, нуждаются в информации, способствующей надлежащему исполнению ими своих обязанностей по текущему управлению фирмой с одновременным, максимально возможным и, естественно, постоянно усиливающимся стремлением к удовлетворению собственных интересов, а с другой стороны, вынуждены периодически выдавать некий объем данных (например, в виде периодической отчетности), свидетельствующий о своей профессиональной компетентности с позиции собственников фирмы. [c.11]
Описанная модель представляет собой сетевую параметрическую задачу. Для ее решения используется. метод, условно называемый комбинированным. Он представляет собой итерационный процесс, являющийся синтезом метода Форда-Фалкер-сона для решения задачи о максимальном потоке с венгерским методом решения транспортной задачи. Поскольку сеть формализована, объем дуговой информации значительно сокращается. Программа, реализующая указанный алгоритм, составлена на языке Фортран для машины БЭСМ-6. [c.57]
Изложенная модель сводится к классической задаче о максимальном потоке в сетях. Первоначально для решения такой модели ОДМ применялся специально разработанный для задач о максимальном потоке алгоритм Форда-Фалкерсона [53,1]. В дальнейшем модель ОДМ реализовывалась с использованием метода внутренних точек [36], который оказался особенно уместным в связи с необходимостью решения дополнительной проблемы - пропорционального нагрузкам распределения дефицита мощности по узлам. [c.133]
Заключение. В задаче о максимальной работе, которую можно извлечь из термодинамической системы при отсутствии ограничения на продолжительность процесса, решение не зависит от уравнения состояния системы и кинетики потоков и достигается в обратимом процессе варавнивания интенсивных переменных подсистем при их контакте через рабочее тело. Сама же максимальная работа равна разнице суммарной внутренней энергии в начале и в предельном равновесном состоянии. В обратной задаче о минимальной работе, потребной для приведения системы из равновесного в заданное состояние, решение также соответствует равновесному процессу, а работа превосходит максимальную полученную на величину, компенсирующую необратимость, возникающую в необратимых равновесных процессах подобных процессам смешения. [c.108]
Недостаточным объем выручки может оказаться в следующих случаях первое — продукция продается по цене ниже себестоимости. Происходит это по двум основным причинам неумения правильно рассчитывать цену в рыночных условиях или сознательное занижение цены с целью перевода части расчетов в так называемый черный нал для ухода от налогообложения. Этот вариант нередко можно наблюдать в сочетании. Стало типично, когда директор крупного государственного предприятия создает собственное дочернее предприятие по сбыту продукции этого предприятия, чтобы продавать продукцию дочернему предприятию по минимальным ценам. Тогда максимальная прибыль перейдет в руки дочернего предприятия. При этом жадность не знает границ. Директор волевым решением занижает цену готовой продукции с одной стороны, для получения в свой карман максимума прибыли, с другой стороны, для информации коллектива и общества в целом, что государственное предприятие в кризисе и ему необходима поддержка. В таком случае главной задачей менеджера является тщательный анализ денежных потоков и маркетинговое исследование рынка с целью выяснения истинной ситуации. Решение этой задачи часто затрагивает крупные денежные интересы, поэтому необходимо заранее побеспокоиться о собственной безопасности. [c.208]
Смотреть страницы где упоминается термин Задача о максимальном потоке
: [c.274] [c.41]Введение в экономико-математическое моделирование (1984) -- [ c.188 ]
