Экстремум функции двух переменных [c.305]
| Рис. 15.1. Экстремум функции двух переменных | 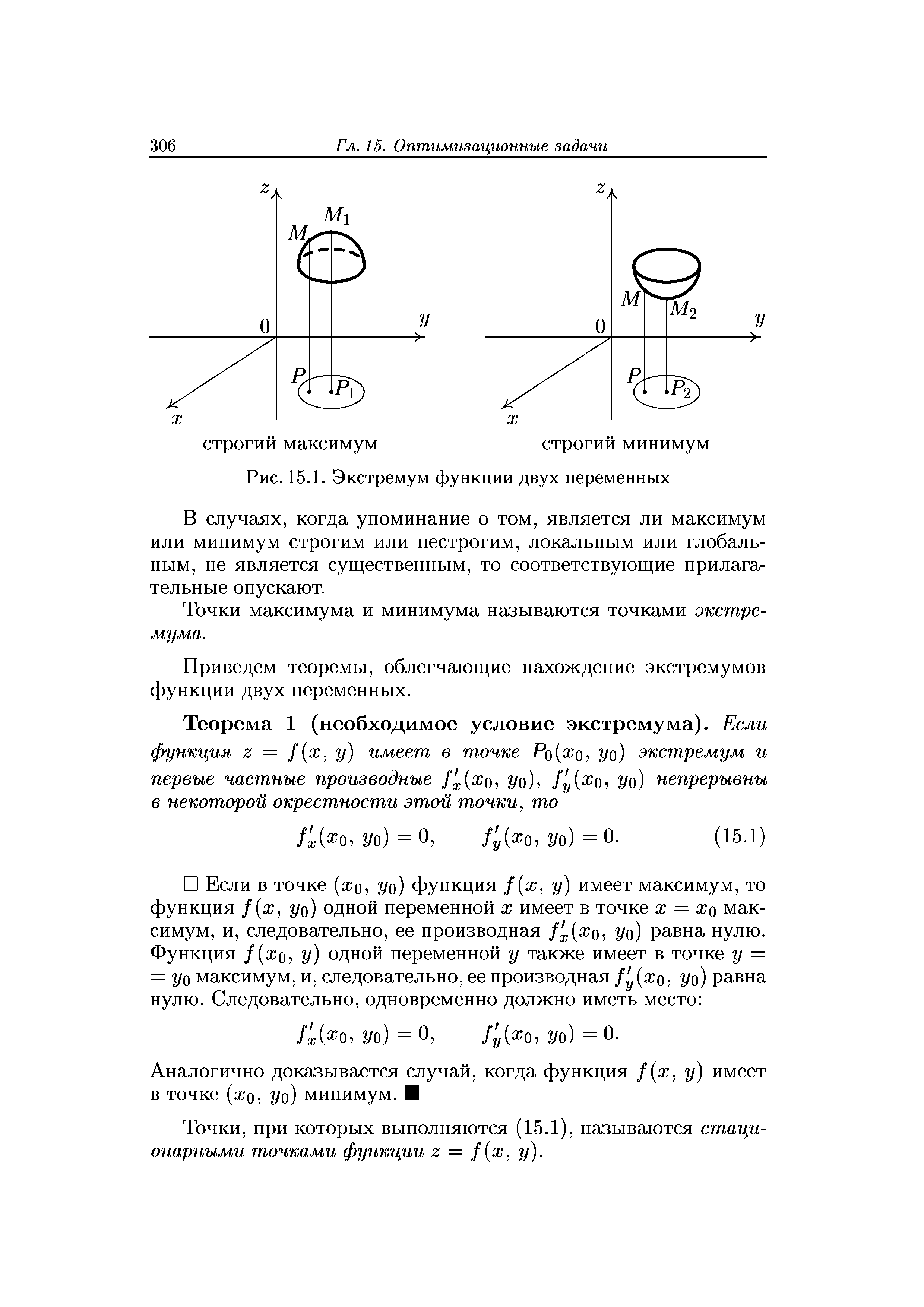 |
Отметим, что теорема 3 (о достаточных условиях экстремума функции двух переменных) из предыдущего пункта является следствием теоремы 2, поскольку введенный в предыдущем пункте определитель А является гессианом функции двух переменных. [c.316]
В предыдущей главе (с. 305) были рассмотрены методы поиска экстремумов функции двух переменных. В настоящем параграфе рассмотрены некоторые приложения этих задач к задачам экономии ресурсов. [c.353]
Задача выбора оптимальных темпов выполнения работ (z/p) и количества ЛОСП (qp) может быть сведена к нахождению экстремума некоторой поверхности, как функция двух переменных Э=/ (у, q). Данная функция является дискретной, но вместе с тем значения этой функции мало изменяются при изменении количества объектных потоков. Это обстоятельство позволяет при оптимизации считать данную функцию непрерывной. Погрешность при нахождении экстремума, как показывают проверочные расчеты,, составляет 3 — 5%. [c.44]
Достаточные условия экстремума. Отметим, что окрестность, минимум, максимум и экстремум для функции многих переменных определяются аналогично тому, как это сделано для функции двух переменных. Так же как и в случае функции двух переменных, доказывается [c.313]
В этом параграфе будет показано, что принцип максимума содержит полную совокупность необходимых условий экстремума первого порядка в том же смысле, в каком для функции двух переменных / (х, у) соотношения fx—0, fff=Q образуют полную систему необходимых условий, а равенство fx=Q является необходимым условием, но полной системы не образует. Более точно этот факт может быть сформулирован следующим образом [c.79]
Сформулируйте определение локального и глобального экстремума функции двух и п переменных. Может ли глобальный экстремум не быть локальным [c.119]
Достаточные условия экстремума функции можно сформулировать и на языке квадратичной формы, изучаемой в разделе Аналитическая геометрия и линейная алгебра . Достаточные условия экстремума функции многих (и не только двух) переменных сводятся к положительной (или отрицательной) определенности квадратичной формы [c.310]
Отметим, что если известен график Ff функции Дх, ) двух переменных х, и х2, то, глядя на него, можно сразу понять, есть ли точки абсолютного и условного локального экстремума или какие-то из них (а, возможно, все) отсутствуют. [c.122]
Естественным является следующий способ решения задачи (5 ,(6) на условный экстремум. Выразить из уравнения (6) переменную х2 через переменную х, и подставить полученное выражение Xj = 1 - х, в функцию (5). Тогда задача (5),(6) на условный экстремум функции (5) двух переменных сведется к задаче на безусловный экстремум функции у — 2х,2 - 2х, + 1 одной переменной х,. [c.123]
Весовые коэффициенты ja и 7 соответствуют доле общего времени цикла, в течение которой раствор вступает в контакт с источником в абсорбере и десорбере соответственно. Задача (5.119), (5.120) путем преобразований сводится к поиску экстремума функции двух переменных — nd и qd [c.206]
Задача 4.1. Исследовать на экстремум следующую квадратичную функцию двух переменных y=xl2-2xlx2+2x22-xl-2xr Эту задачу предлагается решить самостоятельно. [c.117]
Так как Y = -L, то Y = 10 и X = 10. Максимальное произведение 10 10= 100. Метод множителей Лагранжа был продемонстрирован для двух переменных и одной 01раничительной функции. Метод можно также применять, когда есть более чем две переменные и более чем одна ограничительная функция. Далее для примера следует форма для поиска экстремума, когда есть три переменные и две ограничительные функции [c.187]
Задачи линейного программирования для двух переменных могут быть решены с помощью построения графиков. В 1940-х годах Данциг разработал алгоритм, называемый симплексным алгоритмом, эффективно преобразующий графический подход в алгебраический метод, который может быть использован для компьютерного приложения и позволяет обрабатывать любое число переменных. Симплексный алгоритм — это итерационный процесс нахождения оптимального значения (экстремума) целевой функции. [c.428]
Однако, к сожалению, выразить аналитически переменную х2 через переменную х, (или переменную х, через переменную х2) часто бывает сложнб, а то и невозможно. По этой причине только что описанная простая идея сведения задачи на условный экстремум для функции (1) двух переменных к задаче на безусловный экстремум для функции Дх,, А(х,)) одной переменной не может быть использована в качестве основы универсального метода решения задачи (1),(2) на условный экстремум. [c.124]
Задача (1), (2) называется задачей на условный локальный максимум (минимум). Термин условный здесь появляется в связи с тем, что независимые переменные х, и х2 удовлетворяют условию (ограничению) (2). Вместо двух терминов (максимум и минимум) используется обобщенный термин экстремум. В задаче (1), (2) на условный экстремум функциюДх , ) принято называть целевой, ибо ее максимизация (или минимизация) часто есть формальное выражение какой-то цели (например, максимизации объема производства при фиксированных затратах). Функцию g называют функцией, задающей ограничение, или функцией связи. [c.120]
