На более длинных частотах рынок реагирует на экономическую и фундаментальную информацию нелинейным образом. Кроме того, предположение о том, что рынки и экономика должны быть связаны, не является неразумным. Это подразумевает, что нелинейная динамическая система была бы подходящим способом моделирования взаимодействия, удовлетворяющим тот аспект гипотезы фрактального рынка, который остался нерешенным с помощью дробного броуновского движения. Нелинейные динамические системы прибегают к непериодическим циклам и ограниченным множествам, называемым аттракторами. Сами системы подпадают под классификацию хаотических систем. Тем не менее, для того чтобы называться хаотическими, они должны отвечать очень специфическим требованиями. [c.228]
На основании результатов из предыдущих глав кажется, что шумовой хаос является разумным объяснением движений рынка капитала. За исключением валюты, шумовой хаос совместим с долгосрочным, фундаментальным поведением рынков, а дробное броуновское движение более совместимо с краткосрочными торговыми характеристиками. Оба типа поведения совместимы с гипотезой фрактального рынка, описанной в Главе 3. [c.240]
| Рис. 7.4. Д/5-анализ фрактальное броуновское движение. Факт ческое Н = 0.72, оценка Я = 0.73. | 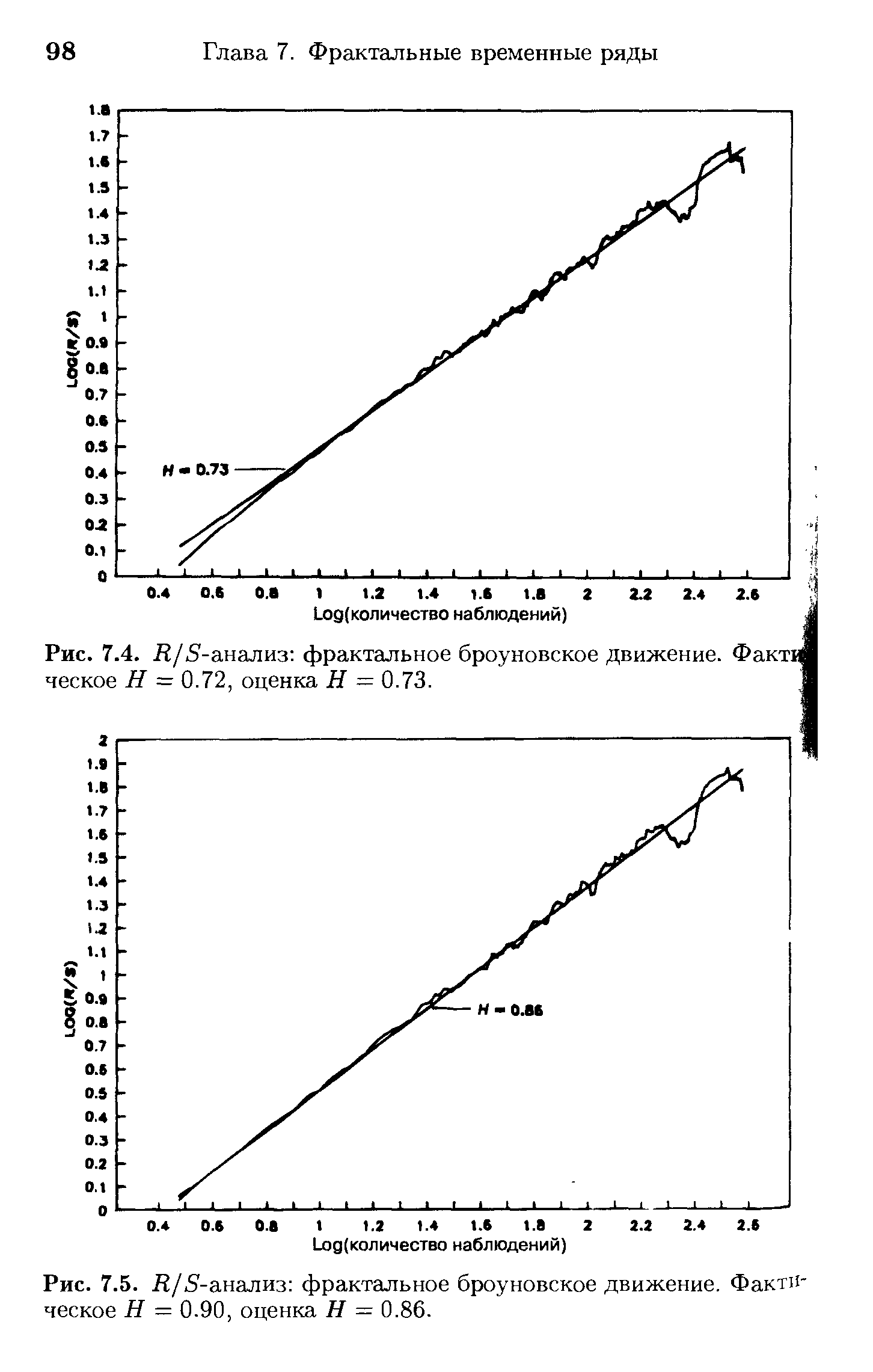 |
| Рис. 7.5. Д/5-анализ фрактальное броуновское движение. Фактическое Я = 0.90, оценка Я = 0.86. | 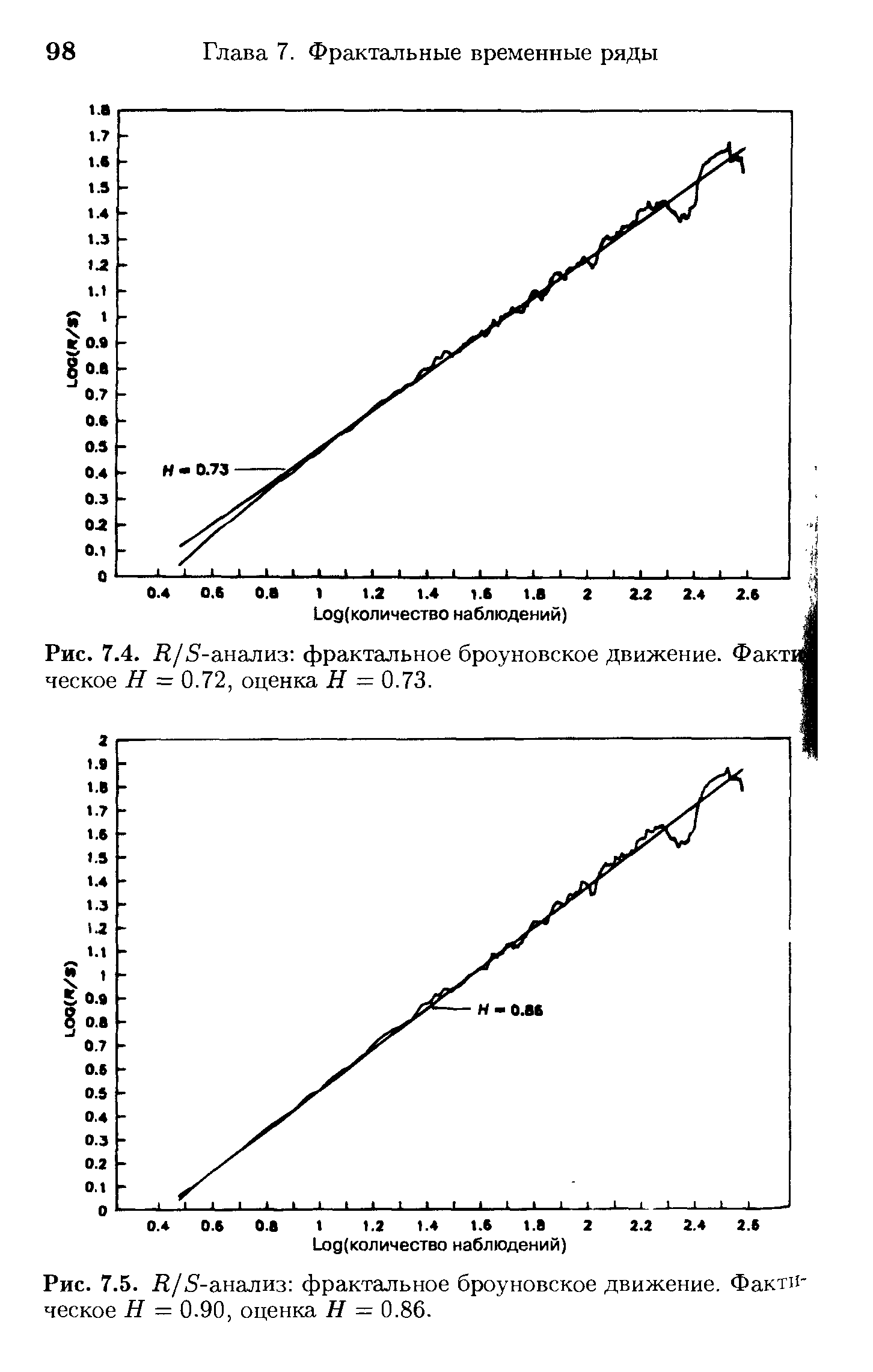 |
Фрактальное броуновское движение....................277 [c.230]
Фрактальное броуновское движение [c.277]
Фрактальное броуновское движение. Рассмотрим функцию [c.278]
Из данного определения следует, что (стандартное) фрактальное броуновское движение X — (Xt)t>o удовлетворяет следующим свойствам, [c.279]
Замечание 4. В теории случайных процессов хорошо известна роль семимартингалов как того класса, для которого развита теория стохастического исчисления (см. далее раздел 5 и, подробнее, например, [250], [304]). В этой связи полезно отметить, что фрактальное броуновское движение БЯ с 0 < Ы < 1 we является (за исключением Н = 1/2, т. е. случая броуновского движения и Н = 1) семимартингалом. Доказательство этого факта для 1/2 < Н < 1 см. в монографии [304 гл. 4, 9, пример 2]. [c.282]
Имея в виду применение фрактального броуновского движения к описанию динамики финансовых индексов, выберем некоторую единицу измерения времени п = 0, 1, 2,... и положим [c.286]
Полезно заметить, что в случае Н = 1 фрактальное броуновское движение B (t) = Шн(1) (Р-п.н.). И, следовательно, в этом случае последовательность h = (hn) приращений hn = Вп(п) — Вт(п — 1), п 1, носит тривиальный характер все величины Л = -Вн(1), п 1, что можно было бы назвать случаем "идеальной настойчивости" [c.287]
Напомним, что если Н = Вщ - фрактальное броуновское движение, то для всякого А > 0 и f > О [c.418]
Приведенные формулы и соображения, основанные на законе больших чисел, подсказывают естественность введения вариационных характеристик и проведения на их основе статистической проверки того, что процесс Я = (Ht)t Oi участвующий в формировании пен S — (St)t b является автомодельным процессом типа фрактального броуновского движения или а-устойчивого движения Леви. [c.418]
Отметим, что для фрактального броуновского движения Н = Вщ при [c.420]
Замечание 2. Случайные процессы Я = (Я4)4 0) обладающие свойством (23), принято называть процессами нулевой энергии (см., например, [166]). Тем самым, из (22) и (23) вытекает, что фрактальное броуновское движение l/2 < Н 1и строго -устойчивые процессы Леви с Н = 1/а > 1/2 являются процессами нулевой энергии. [c.420]
Замечание. По поводу оценки параметра И для фрактального броуновского движения см. гл. III, 2с, ц. 6. [c.424]
В Части 4 мы исследовали дробное броуновское движение (FBM) как возможную модель для рыночных прибылей. FBM имеет ряд важных характеристик, которые соответствуют гипотезе фрактального рынка. Среди них - статистическое самоподобие стечением времени и персистентность, которая создает тренды и циклы. Статистическое самоподобие соответствует наблюдаемому частотному распределению прибылей, исследованному в Главе 2. Мы видели, что они схожи по форме в различных масштабах времени. Персистентность согласуется с идеей, что на различных инвестиционных горизонтах информация поглощается неравномерно. Наконец, тот факт, что, как оказывается, рыночные прибыли являются черным шумом, в то время как волатильность является розовым шумом, согласуется с теоретической взаимосвязью между этими двумя цветными шумами. [c.225]
Показатель Херста (Н). Мера смещения в частично броуновском движении Н=0,50 для броуновского движения 0,50<Н<1,00 для персистентного или трендоустойчивого ряда 0<Н<0,50 для антиперсистентной или возвратной к среднему системы. Величина, обратная показателю Херста, равна альфе — характеристическому показателю во фрактальных распределениях или распределениях Парето. [c.289]
| Рис. 7.7. Тест на перемешивание для Л/5-анализа фрактальное броуновское движение. Неперемешанные данные Н = 0.86, перемешанные данные Н — 0.52. | 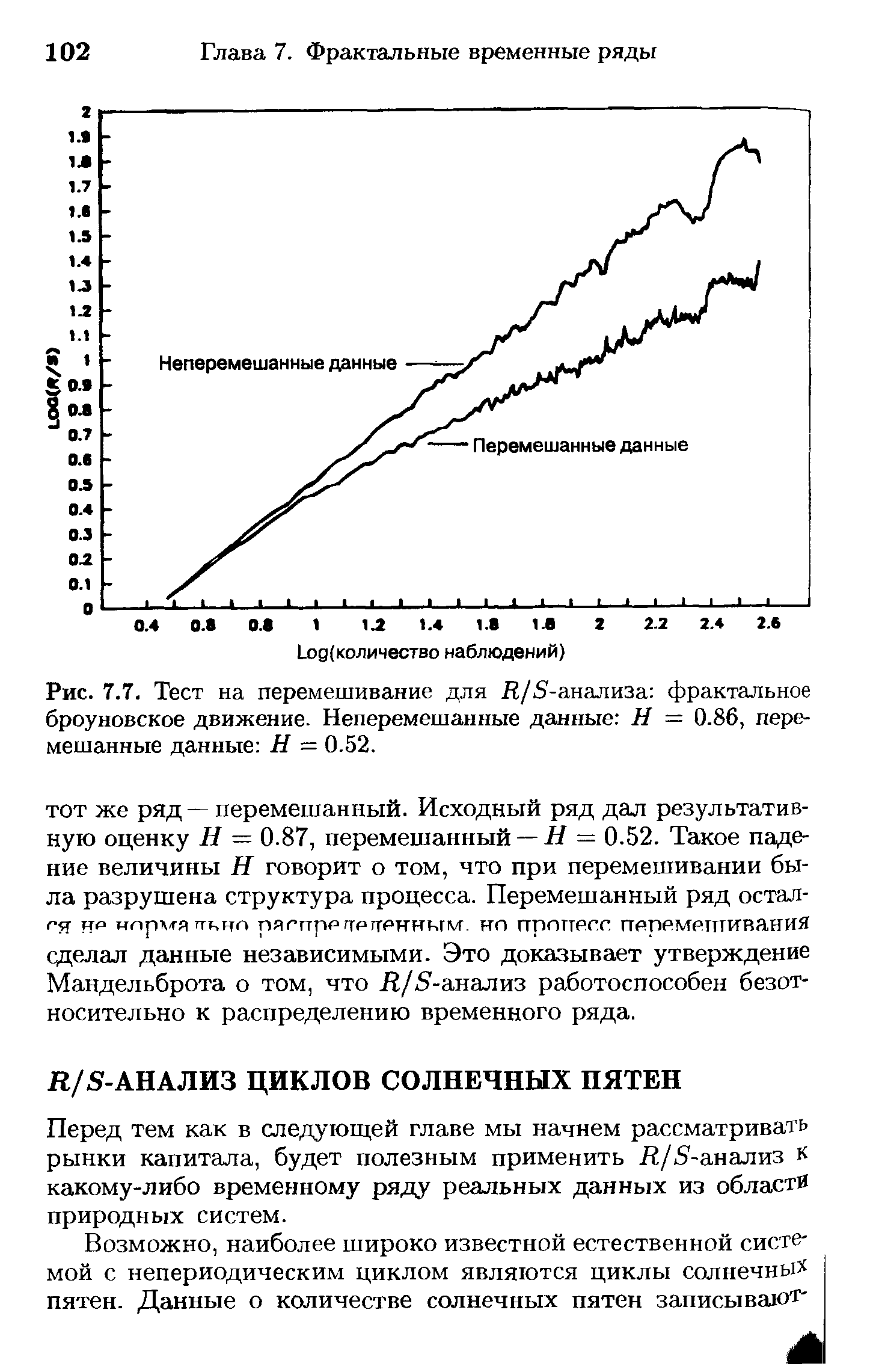 |
Как уже было сказано выше, математически безупречной теорией, которой мыв настоящей книге следуем, является " Теория арбитража". В этой связи следует подчеркнуть, что каждая из концепций эффективности, безарбитражности, фрактальности ни в коей мере не заменяет другую. Они дополняют друг друга, и, например, многие безарбитражные модели обладают фрактальной структурой, а фрактальные пропессы могут быть (относительно мартингальных мер) мартингалами (и тогда соответствующий рынок является безарбитражным), но могут быть и не мартингалами, как, например, фрактальное броуновское движение (см. 2с, гл. Ш). [c.82]
Работы Г. Харста и отмеченные наблюдения явились отправными для Б. Мандельброта, который предложил как в рассматриваемой им модели Харста, так и во многих других вероятностных моделях, в том числе и в финансовой математике, использовать строго устойчивые процессы ( 1с) и фрактальное броуновское движение ( 2с), обладающие свойствами автомодельности. [c.273]
Нужные нам для дальнейшего определения статистической автомодельности и фрактального броуновского движения будут даны в 2с. Следующий же параграф, не связанный непосредственно с финансовой математикой и навеянный материалами работ [104], [379], [385], [386], [428], [456], призван дать общее представление о концепции автомодельности, играющей, как уже отмечалось, центральную роль во фрактальной геометрии. [c.273]
Определение 3. Непрерывныйгауссовскийпроцесс X = (-Xt)t o нулевым средним и ковариационной функцией (5) называется (стандартным) фрактальным броуновским движением с показателем автомодель-ности Харста 0 < Н 1. (В дальнейшем для такого процесса будет часто использоваться обозначение Да = (Дш( ))( о-) [c.279]
Из этих свойств снова следует, что фрактальное броуновское движение обладает свойством автомодельности. [c.280]
Если Н — 1/2, то (стандартное) фрактальное броуновское движение есть не что иное, как (стандартное) броуновское движение, или винеровс-кий процесс. [c.280]
Замечание 2. Почти наверное траектории фрактального броуновского движения Вн удовлетворяют условию Гёльдера с показателем /3 < Н. Они также нигде не дифференцируемы и [c.281]
Для а- устойчивых процессов Леви показатель Харста Н = 1/а, и, следовательно, для таких процессов оценивание Н сводится к оцениванию параметра а. Для фрактального броуновского движения Вт = (Bm(t))t o оценивание параметра Н по дискретным наблюдениям может быть осуществлено, например, следующим образом. [c.283]
Фрактальный шум Л = (Лп) с 0 < Н < 1/2 (розовый шум) имеет отрицательную ковариацию, что, как уже отмечалось, соответствует быстрой перемежаемости в значениях Лп. Именно таким свойством и характеризуются турбулентные явления, что (вместе со свойствами самоподобия) говорит о том, что фрактальное броуновское движение с 0 < Н < 1/2 может служить хорошей моделью для описания турбулентных явлений. [c.287]
Надо, конечно, отметить, что при построении "естественных" (с точки зрения теории финансов) моделей приходится обращаться и к процессам, которые не являются семимартингалами. Типичными в этом отношении является рассмотренное выше ( 2с) фрактальное броуновское движение Вл = (B )t o с любым параметром Харста 0 < Н < 1, за исключением лишь случал Н = 1/2, соответствующего (обычному) броуновскому движению. [c.357]
Как мы видели выше в 3а, для броуновского движения Е Гд = i/2/тгД1/2, для фрактального броуновского движения с показателем Н Е Яд = >/2/7гДн, а для строго а-устойчивого процесса Леви с а > 1 Е ЯД = Е Яг Аи, где И = 1/а < 1. [c.424]
Отметим теперь, что при Н = 1 (стандартное) фрактальное броуновское движение В (t) — t , где и - нормально распределенная случайная величина с нулевым средним и единичной дисперсией. У этого процесса BI = (Bi(t))t o вся "случайность" определяется величиной , и ясно, что в классе всех фрактальных броуновских движений с параметром 0 < Н 1 этот процесс является наименее "зашумленным" Тем самым, становится понятным, что при Н f 1 шумовая компонента у процессов Дц становится "все меньше" а это находит свою "финансовую" интерпретацию в том, что модели, привлекающие для своего описания такие процессы, становятся (при Н t 1) "менее рискованными" (Сформулированному утверждению [c.453]
Все это говорит о том, что эти обменные курсы обладают фрактальной структурой с довольно-таки большим значением параметра Харста. В этой связи полезно напомнить, что для фрактального броуновского движения ЕН% растет как 2И. Поэтому при Н > 1/2 разброс в значениях Ht больше, нежели для обычного броуновского движения, что, конечно, значительно увеличивает риск операций с валютами с ростом времени. Видимо, это объясняет, почему в случае валют предпочтение отдается не долгосрочным операциям, а активному краткосрочному трейдингу. [c.455]
Но это, разумеется, не означает, что семимартингалами "все заканчивается Стохастический интеграл во многих случаях определяется и для несемимартингалов, например, для фрактального броуновского движения и, вообще, для широкого класса гауссовских процессов. Конечно, при этом [c.307]
Фрактальное броуновское движение (Fra tional Brownian motion). Случайно блуждание со смещением его можно сравнить с игрой в кости с использованием фальшивых костей (со смещенным центром тяжести). В отличие от обычного броуновского движения одно из направлений является преимущественным. [c.315]
Пока на рынке присутствуют покупатели и продавцы, будут существовать спрос и предложение на конкретную ценную бумагу. Всегда найдутся желающие купить по цене, которая кому-то кажется разумной, и всегда найдутся желающие продать. Баланс спроса и предложения определяет neiry в каждый конкретный момент времени. Этот баланс подвержен внешним влияниям. Положительные и отрицательные ноности и события изменяют представления игроков о стоимости ценном бумаги и сдвигают баланс в ту или иную сторону. Поскольку каждый инвестор действует по собственным побуждениям, на которые влияет множество внешних и внутренних факторов, цены меняются на первый взгляд достаточно хаотично. Некоторые исследователи фондового рынка утверждают, что движение цен на небольших временных иитсриалах походит на траекторию блужданий броуновской частицы. В гл. 19 было показано, что это не так. Необходимо различать понятия хаоса и фрактальности, случайности и обусловленности. Мы еще вернемся к этой теме в частях VI и VII, где будут рассматриваться особенности торговли на коротких временных интервалах. Что же касается больших интервалов времени, то здесь нет места хаосу. Более того, сам предмет настоящей главы — тренды ценных бумаг — достаточно красноречиво опровергает представления сторонников теории хаоса. [c.248]
