Таблица дисперсионного анализ

Постройте таблицу дисперсионного анализа для расчета значения F-критерия Фишера.  [c.32]

Постройте таблицу дисперсионного анализа для оценки значимости уравнения регрессии в целом.  [c.35]


Составить таблицу дисперсионного анализа для проверки при уровне значимости а = 0,05 статистической значимости уравнения множественной регрессии и его показателя тесноты связи.  [c.61]

По данным таблиц дисперсионного анализа, представленным на рис. 2.9 и 2.10, факт =151,65. Вероятность случайно получить  [c.76]

Согласно данным таблицы дисперсионного анализа см. рис. 4.21), полученные значения -критерия Фишера и коэффициента детерминации Л2 показывают высокий уровень аппроксимации исходных данных.  [c.163]

Оценка значимости уравнения регрессии обычно дается в виде таблицы дисперсионного анализа (табл. 2.2).  [c.53]

Расчет F-критерия можно вести и в таблице дисперсионного анализа результатов регрессии, как это было показано для линейной функции (см. табл. 2.2).  [c.85]

Чтобы получить частный. F-критерий для факторах,, необходимо рассмотреть другую таблицу дисперсионного анализа, в которой оценивается дополнительный вклад фактора х, после включения в модель фактора х2 (табл. 3.3).  [c.135]


Если уравнение содержит больше двух факторов, то соответствующая программа P дает таблицу дисперсионного анализа, показывая значимость последовательного добавления к уравнению регрессии соответствующего фактора. Так, если рассматривается уравнение  [c.136]

Таблица дисперсионного анализа  [c.340]

ТАБЛИЦА 10.6. ТАБЛИЦА ДИСПЕРСИОННОГО АНАЛИЗА  [c.173]

Таблица дисперсионный анализ  [c.615]

Таблица 7.9 Схема однофакторного дисперсионного анализа Таблица 7.9 Схема однофакторного дисперсионного анализа
Таблица 7.10 Схема двухфакторного дисперсионного анализа Таблица 7.10 Схема двухфакторного дисперсионного анализа
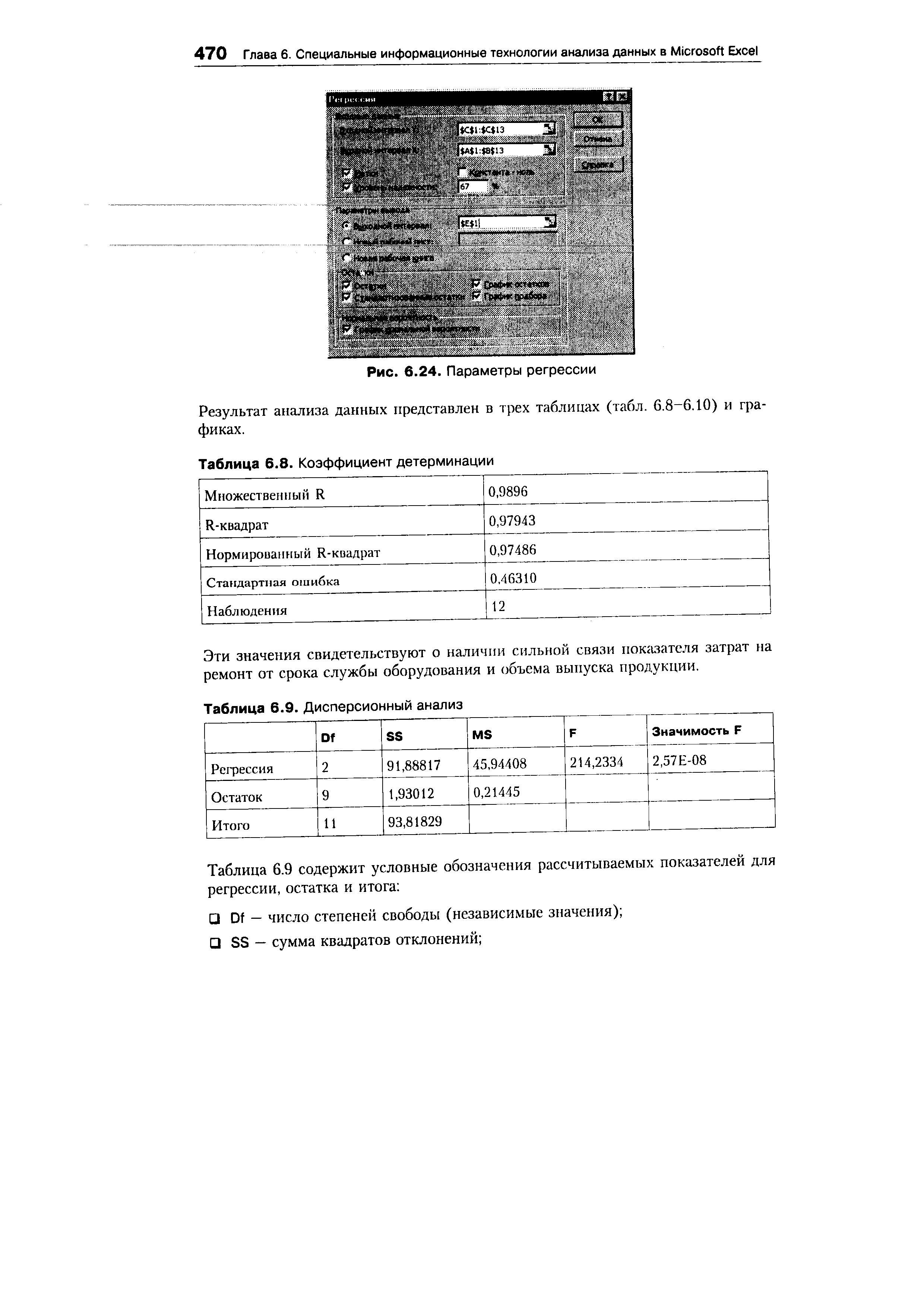Таблица 6.9. Дисперсионный анализ Таблица 6.9. Дисперсионный анализ
Первичный анализ может быть описательным и представлять табличные данные, на основе которых выводят или рассчитывают такие показатели, как средние уровни, стандартные отклонения и частости, либо сравнительным, то есть содержать, например, сопоставительные таблицы. В более сложных случаях используют методы поиска корреляции, например регрессионный анализ. Для установления причинно-следственных соотношений применяют, например, дисперсионный анализ экспериментальных данных.  [c.68]

Составьте таблицу результатов дисперсионного анализа.  [c.81]

Постройте таблицу результатов дисперсионного анализа. Оцените значимость построенной модели.  [c.159]

Таблица 3.2 Дисперсионный анализ для оценки существенности фактора хг 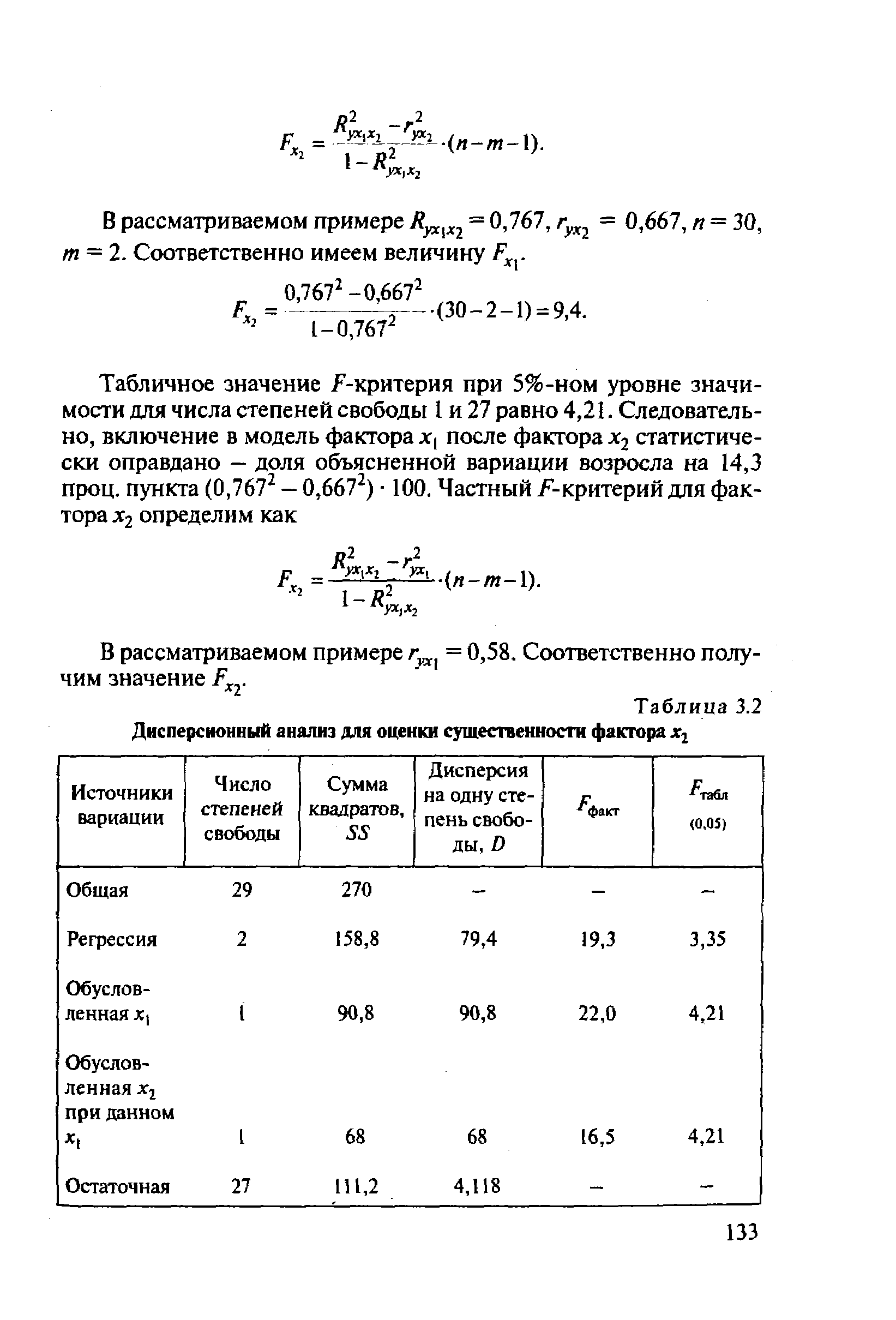Таблица 3.2 <a href="/info/3034">Дисперсионный анализ</a> для оценки существенности фактора хг
Табл. 3.2 отличается от таблиц результатов дисперсионного анализа, рассматриваемых ранее (см., например, табл.3.1). В ней источник вариации регрессия раскладывается на две составляющие 1) обусловленная влиянием фактора j ( 2) обусловленная дополнительным включением в регрессионную модель фактора х2. Соответственно в нашем примере число степеней свободы за счет регрессии, равное 2, также раскладывается на число степеней свободы для каждого фактора, т. е. 1 для фактора х, и 1 для фактора х2. Сумма квадратов за счет регрессии  [c.134]


Таблица 3.3 Дисперсионный анализ для оценки существенности фактора ж, 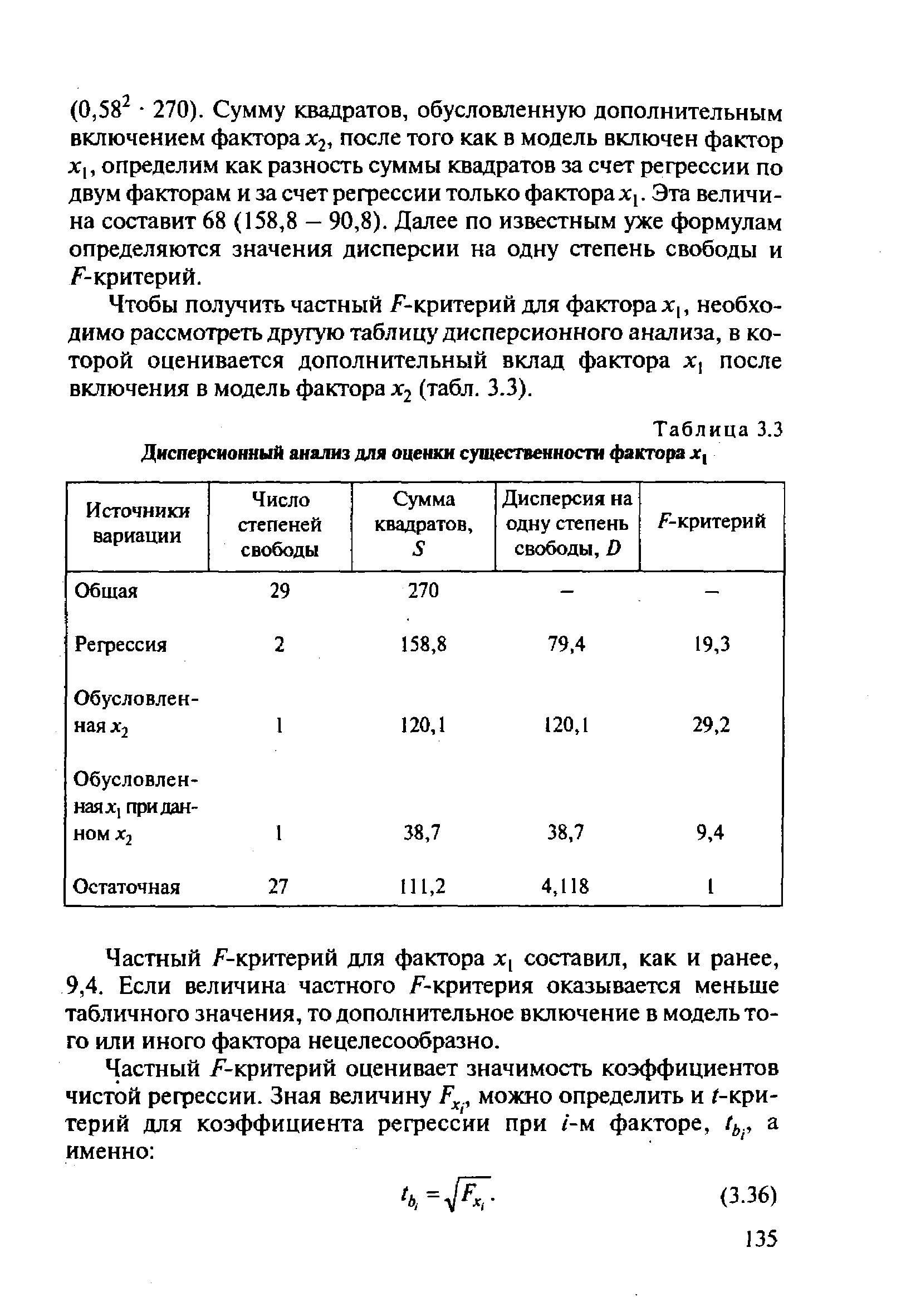Таблица 3.3 <a href="/info/3034">Дисперсионный анализ</a> для оценки существенности фактора ж,
Таблица 5.5. Дисперсионный анализ для ц Таблица 5.5. Дисперсионный анализ для ц
Таблица 11.2. Дисперсионный анализ на основе аккумуляционного Таблица 11.2. <a href="/info/3034">Дисперсионный анализ</a> на основе аккумуляционного
Таблица 14.3. Результаты дисперсионного анализа дисперсионных Таблица 14.3. Результаты <a href="/info/3034">дисперсионного анализа</a> дисперсионных
Таблица 14.4. Результаты дисперсионного анализа для эффектов Таблица 14.4. Результаты <a href="/info/3034">дисперсионного анализа</a> для эффектов
Особое значение информационной статистики заключается в том, что для таблиц с многосторонней группировкой она может быть разложена на аддитивные составляющие, соответствующие различным гипотезам. При этом может быть построена теория, во многом параллельная дисперсионному анализу (см. гл. 13).  [c.129]

Методы статистического исследования зависимостей, в особенности регрессионный анализ, анализ временных рядов, дисперсионный анализ, анализ таблиц сопряженности, планирование эксперимента, наиболее употребительны среди методов обработки данных в различных областях науки и техники. Соответственно к настоящему времени существует и продолжает разрабатываться обширное программное обеспечение, связанное с исследованием зависимостей. Ниже кратко рассмотрены программные средства — пакеты и библиотеки программ, доступные пользователям в СССР, а также наиболее интересные, на наш взгляд, для обеспечения статистического исследования зависимостей зарубежные пакеты и библиотеки. Основные сведения о пакетах и библиотеках программ приведены в табл. 15.1.  [c.425]

В факторных планах используются методы дисперсионного анализа. Эти планы позволяют измерять влияние взаимодействий, но методика в достаточной мере сложна. Она заключается в построении таблицы, содержащей всевозможные комбинации различных факторов. Например, для четырех факторов, каждый из которых может находиться на 3, 2, 5 и 3 уровнях, соответственно существует 3X2,  [c.192]

Совместные распределения количественных признаков. Условные распределения. Независимость признаков. Критерий Пирсона. Таблица сопряженности. Регрессионный и корреляционный анализ. Метод наименьших квадратов. Коэффициент корреляции. Дисперсионный анализ однофакторный, многофакторный без повторений. Анализ временных рядов. Тренд, сглаживание, сезонность, циклы. Стационарные ряды. Динамические регрессии. Ложная регрессия. Коинтеграция.  [c.49]

Таблица 3 Дисперсионный анализ для одного фактора с / наблюдениями в ячейке 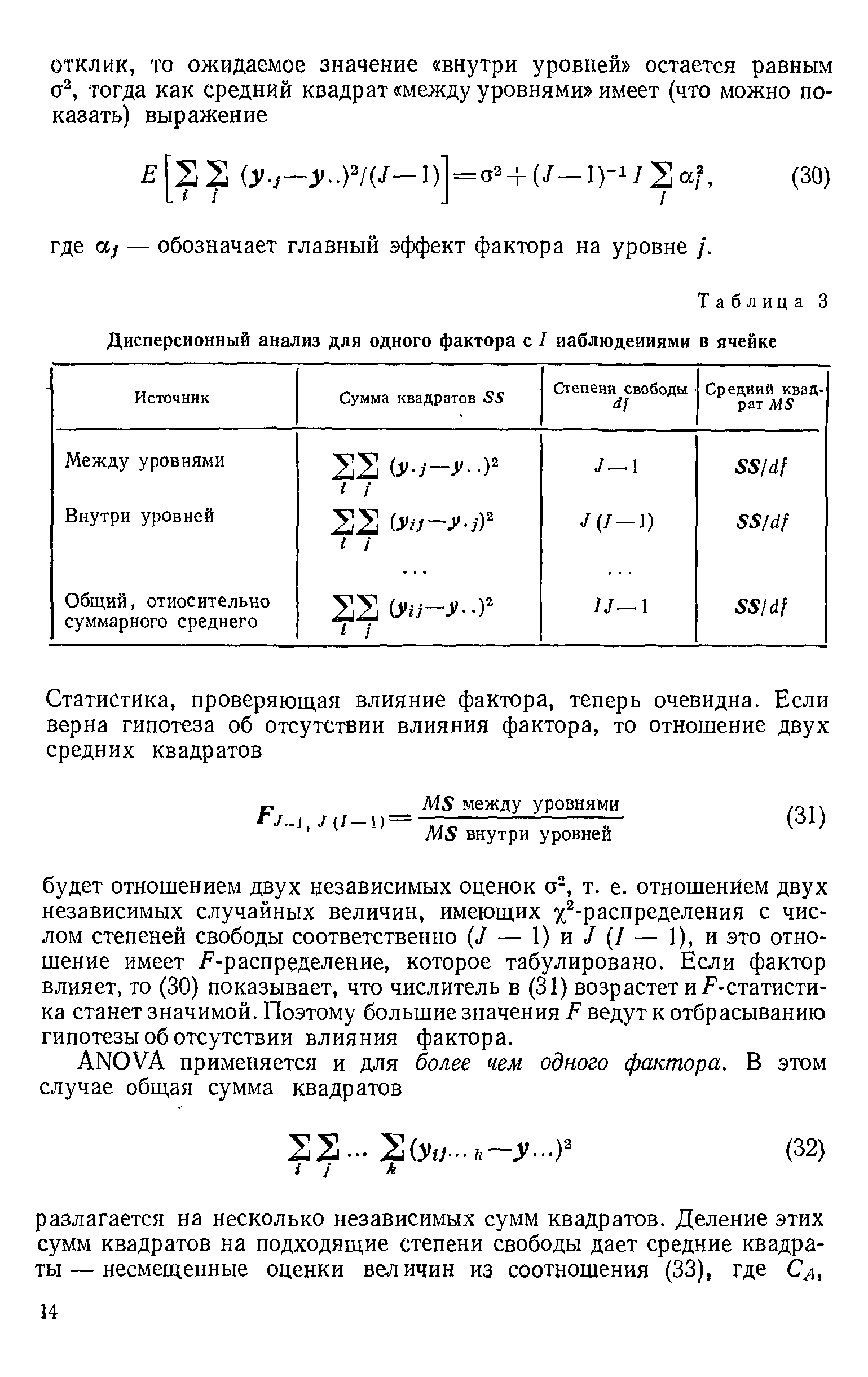Таблица 3 <a href="/info/3034">Дисперсионный анализ</a> для одного фактора с / наблюдениями в ячейке
В VI.9 мы рассмотрим несколько методов отыскания важных факторов, т. е. таких факторов, которые приводят к потере работоспособности ММР. Показано, что первый метод, который использует таблицы сопряженности признаков, неприемлем. Второй метод заключается в применении биномиального критерия вероятности того, что в отброшенных комбинациях фактор, имеющий один и тот же уровень, тем не менее не важен. Показано, что эти критерии, однако, имеют малую мощность. Третий метод—это регрессионный анализ. Будут исследованы обычные предпосылки регрессионного и дисперсионного анализа и будет показано, почему простой метод наименьших квадратов предпочтительнее обобщенного метода. Мы оценим коэффициенты регрессии или эффекты , проверим адекватность уравнения регрессии (если Р 0,90, будет провозглашена адекватность), значимость отличия коэффициентов регрессии от нуля (фактор 1 даст нулевой эффект, фактор 5, может быть, тоже имеет нулевой эффект).  [c.270]

Верхняя строка корректированный / -квадрат = 0,872390 вторая строка / -квадрат = 0,897912 третья строка множественный R = 0,947582. Затем приводится таблица дисперсионного анализа, в которой указываются источники вариации объясненная сумма квадратов отклонений значений, рассчитанных по уравнению регрессии, от среднего значения DlfnM il = Z(p/ - у)2 = 662 772,98 при числе степеней свободы, равном числу объясняющих переменных dfk = 3 остаточная - отклонения фактических значений от расчетных Dwm Z(y/ - у)2 = 75353,96 при числе степеней свободы, равном df=n-k-, df= 2 общая - ZO/ - У = 738 126,94, при числе степеней свободы df = п - 1, df = 15. Затем приводится средний квадрат отклонений s = Д , с//)6ы, , = 662772,98 3 = 220924,3 s г = D,Km dfwm, = 75353,96 12 = 6279,5. Далее указано их отношение, т. е. 5, /г2 = F-критерию. Наконец, указывается вероятность ошибочного решения, т. е. нулевого / 2, равная 0,000003171.  [c.277]

Припишем численные значения оценкам vl — хорошо, v2 — удовлетворительно, v3 — неудовлетворительно. Тогда набранные лабораториями оценки можно представить в виде односторонней таблицы дисперсионного анализа (см. гл. 13), в которой СКП — полная сумма квадратов отклонений, СКМ — сумма квадратов отклонений между лабораториями и СКВИ — сумма квадратов отклонений внутри лабораторий (табл. 3.3)  [c.133]

Вопрос 4. При проведении эксперимента, используя сырье, поставленное тремя фирмами A , AZ, А8, измерили предел прочности при растяжении в условиях Bj, когда предварительная обработка не проводилась, в условиях Ва, когда предварительная обработка проводилась, и с применением соответствующих способов работы GI, Са. При этом 12 раз рандомизированно осуществлялись испытания. В результате были получены значения, приведенные в таблице. Проведите дисперсионный анализ.  [c.189]