Все три кривые имеют асимптотами оси координат, хотя и приближаются к ним. с разной скоростью. Это [c.62]
Эта кривая имеет две асимптоты. При L - + °° основные фонды К постоянно убывают, но стремятся не к нулю, как в случае функции Кобба — Дугласа, а к некоторому положительному числу [c.64]
Эта кривая имеет асимптоту, т. е. при бесконечном росте фондовооруженности производство не растет неограниченно, как в случае функции Кобба — [c.65]
Дугласа. Сам факт существования асимптоты легко доказать. Действительно, [c.65]
Это свойство отражает тот же факт, что и наличие асимптот у изоквант в случае ограниченности одного из ресурсов нельзя достигнуть любого наперед заданного националь- [c.65]
Поскольку функция с постоянной эластичностью замены, как показано в предыдущем параграфе, имеет горизонтальную асимптоту у — уп (1 — у.) р при k -ч оо, то при достаточно больших k имеем [c.76]
Для функции Кобба — Дугласа также можно показать, что ф (k) < 0 при достаточно больших значениях k. Хотя функция Кобба — Дугласа и не имеет асимптоты при k - оо, при достаточно больших справедливо соотношение [c.76]
Эти функции имеют много общего они равны нулю при х = О, монотонно возрастают, вогнуты. Есть, однако, два важных различия предельная эффективность г/ (30 функции (3.10) при ж- -0 не стремится к бесконечности, а при х-++°° не стремится бесконечности сама функция у (50 она ограничена асимптотой У = Рз Поскольку х = х,/х2, то сильное отличие функции (3.10) от степенной функции при больших и малых значениях х означает, что функция (3.9) отличается от степенной свойствами замещения одного ресурса другим. [c.88]
Эта изокванта изображена на рис. 2.8. При xt -> °° она имеет асимптоту жг = (г/0/6)р2 Р. Это означает, что даже при неограниченном росте количества первого ресурса для выпуска продукции в количестве z/0 необходим второй ресурс в количестве, большем (г/0/6)р2 Аналогичная ситуация складывается при увеличении [c.88]
Каждому конкретному уровню доходов и цен, по мнению Парето, соответствуют несколько наборов благ с одинаковой полезностью U., которые графически представлены на рис. 11.3—11.4 различными гиперболами, образованными в сечениях конической поверхности. Проекции их асимптот на плоскость qt(n, 0, <72(/) — суть оси координат плоскости первого квадранта. [c.236]
В свою очередь пределом накопленного роста ресурсов и запасов категорий С3 и С2 является оценка НСР на соответствующий момент времени. В разрезе пятилетнего планирования такая последовательность движения ресурсов приводит к тому, что на момент планирования объем возможной добычи предопределен на три пятилетки вперед (рис. 6). Если планирование начинается с задания плана добычи на момент t0, то оценка асимптоты аппроксимирующей кривой определит необходимый уровень состояния запасов категорий А + В + Q на момент предшествующей пятилетки и т. д. [c.23]
Во многих случаях для аппроксимации нелинейной зависимости очень удобно использовать гиперболу, однако зачастую об этом трудно догадаться. Дело в том, что мы легко узнаем только простую гиперболу, асимптотами которой являются оси координат, то есть у = a I x. Если эта гипербола сдвинута вдоль одной из осей или вдоль обеих осей, то ее как правило не узнают. [c.130]
Большинство методов, рассматриваемых в этой книге, эффективны при долгосрочных стратегиях. На протяжении всей книги вы будете встречать термин асимптотический смысл , что означает возможный результат чего-либо, осуществленного бесконечное число раз, когда вероятность приближается к определенности при увеличении количества попыток. Другими словами, что-то, в чем мы можем быть почти уверены с течением времени. Смысл этого выражения содержится в математическом термине асимптота , которая является прямой и ограничивает кривую линию в том понимании, что расстояние между двигающейся точкой кривой и прямой линией приближается к нулю, когда точка удаляется на бесконечное расстояние от начала координат. [c.5]
Другое расхожее заблуждение состоит в том, что будто бы увеличение числа компонентов портфеля снижает его эффективность, или что в пределе выгода от увеличения числа компонентов убывает, то есть достигает некоторой асимптоты. Это не так кривая зависимости между этими факторами отличается от логарифмической и, скорее всего, представляет собой прямую линию, поднимающуюся снизу вверх и слева направо, ибо с помощью диверсификации мы достигаем только увеличения Т. Всякий прирост Т соответствующим образом увеличивает прирост счета, который не имеет асимптот. [c.69]
С помощью элементарной экстраполяции легко убедиться, что этим данным удовлетворяет гиперболическая функция роста с сингулярностью. Асимптота, по которой наша популяция взлетит в бесконечность, располагается где-то в середине следующего столетия [c.98]
Имейте в виду, что этот график и эти показатели роста популяции получены после таких катастроф, как эпидемия черной смерти четырнадцатого века, которая истребила почти две трети населения Европы, после двух мировых войн (последняя уничтожила около пятидесяти миллионов человек, из которых двадцать семь миллионов приходится только на одну Россию ) и всего остального, чем природа наказывала нас между делом. То есть даже нечто столь катастрофическое, что стерло бы с лица Земли две трети Европы, сегодня привело бы лишь к небольшому временному сдвигу этой асимптоты вперед. [c.98]
| Рис. 2.З. Оптимальное f в качестве горизонтальной асимптоты. | 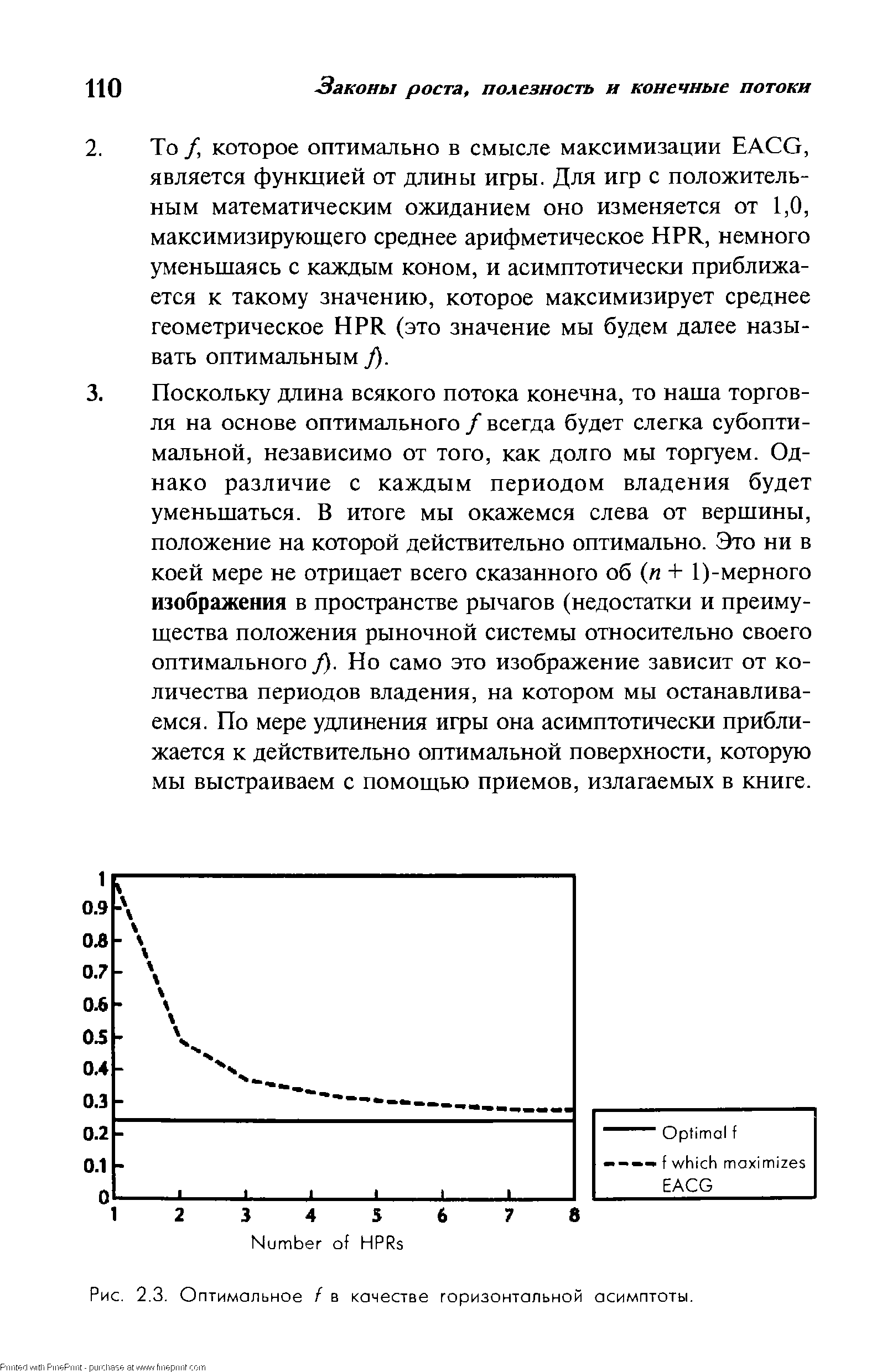 |
При b < 0 имеем медленно повышающуюся функцию с верхней асимптотой при х - оо, т. е. с максимальным предельным [c.67]
Вертикальная асимптота в левой части графика ДО на рис. [c.116]
С — нижняя асимптота, т. е. предел, с которого начинается [c.47]
Если найти из этих уравнений параметры- а и Ь, то можно составить ряд величин (а + Ьх), равных теоретическим значениям lg (Л/(ух- Q - 1). Определяя величины А/(ух - С) - 1), легко составить ряд теоретических значений функции ух. Если С = О, а верхняя асимптота = 100%, или 1, то уравнение логистической функции упрощается до формы [c.48]
В теории вероятностей выборочная Д. с увеличением числа наблюдений асимптотически приближается (см. Асимптота) к теоретической. Это свойство называется состоятельностью оценки Д. [c.89]
Соответствие у=/[х) между переменными величинами, в силу которого каждому рассматриваемому значению некоторой величины х аргумента или независимой переменной) соответствует определенное значение другой величины, у (зависимой переменной или Ф. в значении 1). Ф. задана, если известен закон, определяющий такое соответствие. На практике она задается формулой, таблицей или графиком (есть и другие способы, напр. алгоритмический — см. Алгоритм). При построении графика функции анализируются такие ее свойства, как четность или нечетность, нулевые значения, периодичность (см. Периодическая функция), монотонность (см. Монотонная функция), наличие асимптоты и др. [c.379]
Причем это изменение (уменьшение) не ограничено, как в случаях (4.71) и (4.72), асимптотой. Темп замедления, все более уменьшаясь с ростом х, минует нулевое значение. При дальнейшем росте х это уменьшение будет идти по области отрицательных чисел. Иными словами, при определенном значении х уменьшение превращается в свою противоположность, став отрицательным уменьшением, т. е. увеличением. Таким образом, параболическая зависимость удельных производственных затрат от размеров производства соответствует случаю, когда при увеличении мощности сверх некоторых пределов наблюдается увеличение удельных производственных затрат. [c.171]
Асимптоты графика функции [c.164]
В предыдущих параграфах мы изучали характерные точки. Теперь рассмотрим характерные линии, именуемыми асимптотами. [c.164]
Графики, приведенные на рис. 10.3, — это семейство гипербол, ка дая из которых, если не принимать во внимание ненормальные случаи, стре мится к своей асимптоте КР1/КА, находящейся в пределах 0 < КР1/КА < . что вполне естественно, так как случаи КР1<КД являются преобладаю щими при достаточной статистике. Ситуаций, когда КР1ЖЛ эпизодичн] и кратковременны. [c.212]
Изображенное на рис. 10.3 семейство гипербол было получено nyrei искусственной линеаризации зависимостей A /A Q и Р/ /А. тоб) проследить принципиальную взаимосвязь между At и PL. Для каждого кон кретного случая это функция, близкая к гиперболической, с асимптотой являющейся отношением приростов PI. ( ) к Aff). [c.212]
При выборе кривой следует определять, может ли данное явление (процесс) насыщаться, т. е. приближаться к пределу. Например, гиперболическая функция, модифицированная экспоненциальная функция, кривая Гомперца, логическая кривая имеют асимптоту и могут применяться лишь для аналитическое го выравнивания процессов, имеющих тенденцию к насыщению,. т. е. ограниченных в своем росте. [c.29]
Более наглядное представление о динамике разведанной части ресурсов и добычи дают так называемые кривые освоения ресурсов. В работах [48, 6, 27, 18, 24] оценка НСР принималась в качестве асимптоты, ограничивающей рост накопленных запасов и добычи. К. С. Баймухаметов и М. М. Саттаров предложили при построении кривой накопленных запасов учитывать лишь достоверную часть НСР, а также анализировать кривые освоения запасов различных категорий. М. Д. Белонин и др. [4] более детально исследовали временной аспект в освоении ресурсов нефти и газа различных категорий ло пятилеткам. [c.22]
Исследование динамики социальных и экономических процессов выявило довольно сильную распространенность эффекта насыщения выхода на асимптоту при достижении определенных значений показателей. В силу этого в эконометрике большое распт ространение получили так называемые кривые с насыщением. К этому типу кривых относится кривая Гомперца — s-образная кривая, предложенная Б. Гомперцем (1799—1865), которая имеет вид [c.20]
АСИМПТОТА [asymptote] — прямая, к которой стремится (никогда не достигая ее) имеющая бесконечную ветвь кривая некоторой функции, когда ее аргумент приближается к некоторому заданному значению, неограниченно возрастает или уменьшается. Напр., в функции у = с + + Их значение у приближается с возрастанием х к величине с сколь угодно близко ("асимптотически стремится к ней"). [c.24]
