Поскольку зависимость оказалась параболической, уравнение применяемости АНН в динамике выглядит так [c.90]
Из рассмотрения зависимостей 7VT (H) следует, что во всех случаях они носят параболический характер и могут быть представлены уравнением [c.67]
Для этого отыскивались уравнения регрессии для линейной, гиперболической и параболической второго порядка форм связи(подробнее вопрос о форме связи изложен ниже). При этом использовались расчеты парных корреляционно-регрессионных зависимостей между суточной загрузкой оборудования и расходом в отдельности топлива, воды, электроэнергии и пара, приходящиеся на единицу целевой продукции. [c.99]
Таким образом, связь между изменением себестоимости единицы продукции в зависимости от загрузки оборудования по сырью более полно описывается параболической второго порядка формой связи (рис. 3.6). [c.105]
Из рис. 2 видно, что между суммарной закачкой воды и суммарным приростом добычи нефти наблюдается параболическая зависимость,-свидетельствующая о существующей тенденции роста удельного расхода воды на [c.87]
По такому же принципу рассчитываются и параметры криволинейного уравнения. Так, в случае параболической зависимости параметры а0, аь а2 находятся по следующей системе нормальных уравнений [c.322]
В качестве примера параболической корреляционной связи рассмотрим зависимость себестоимости молока от продуктивности коров по данным аналитической группировки сельхозпредприятий области (табл. 8.5). В этой же таблице приведены расчетные величины, входящие в уравнения МНК для параболы. [c.264]
У детали или целой конструкции может быть несколько предельных состояний напряжения, деформации, колебания. В зависимости от того, какое предельное состояние лимитирует, будет меняться форма детали. Например, балка, лимитированная напряжением, будет иметь параболический пояс, прогибом — параллельные пояса. 16 [c.16]
При b > 0 и с < 0 кривая симметрична относительно высшей точки, т. е. точки перелома кривой, изменяющей направление связи, а именно рост на падение. Такого рода функцию можно наблюдать в экономике труда при изучении зависимости заработной платы работников физического труда от возраста — с увеличением возраста повышается заработная плата ввиду одновременного увеличения опыта и повышения квалификации работника. Однако с определенного возраста ввиду старения организма и снижения производительности труда дальнейшее повышение возраста может приводить к снижению заработной платы работника. Если параболическая форма связи демонстрирует сначала рост, а затем снижение уровня значений результативного признака, то определяется значение фактора, при котором достигается максимум. Так, предполагая, что потребление товара А (единиц) в зависимости от уровня дохода семьи (тыс. руб.) характеризуется уравнением вида ух = 5 + 6 х - х2. Приравнивая к нулю первую производную у х = 6 — 2 х = 0, найдем величину дохода, при которой потребление максимально, т. е. при х = 3 тыс. руб. [c.64]
Модель параболической зависимости применяется в случае ускоренного убывания результативного признака (показатель у) при равномерном увеличении факторного признака (фактор х). [c.134]
Расчет комплексного показателя конкурентоспособности приводится на основе групповых показателей по экономическим и качественным показателям. В силу того, что зависимость между уровнем качества образца и его ценой носит параболический характер, данный показатель может быть определен по следующей формуле [c.434]
Таковы наиболее обобщенные формы зависимости между доходами и спросом. В аналитических моделях используются для разных статей расходов различные функции (напр., степенная, параболическая и др.). Большую роль [c.381]
Причем это изменение (уменьшение) не ограничено, как в случаях (4.71) и (4.72), асимптотой. Темп замедления, все более уменьшаясь с ростом х, минует нулевое значение. При дальнейшем росте х это уменьшение будет идти по области отрицательных чисел. Иными словами, при определенном значении х уменьшение превращается в свою противоположность, став отрицательным уменьшением, т. е. увеличением. Таким образом, параболическая зависимость удельных производственных затрат от размеров производства соответствует случаю, когда при увеличении мощности сверх некоторых пределов наблюдается увеличение удельных производственных затрат. [c.171]
Параболическая зависимость. В некоторых случаях теоретический и логический анализ показывает, что неравномерное изменение результативного признака должно иметь иной характер. Так, при недостаточном количестве осадков урожайность будет, естественно, очень низкой, а по мере увеличения их количества урожайность будет повышаться. Однако это повышение не будет беспредельным, так как для каждой культуры в данных конкретных условиях есть какое-то оптимальное количество осадков, при котором достигается наиболее высокая урожайность. По мере того как количество осадков будет приближаться к оптимальной величине, рост урожайности будет постепенно замедляться и прекратится совсем при достижении этого оптимума. Дальнейшее увеличение количества осадков может привести к тому, что они окажутся излишними и вредными, в результате чего урожайность будет снижаться. Такого рода зависимость приближенно можно выразить уравнением параболы. Аналогичный характер связи можно ожидать и в ряде других случаев, например для зависимости уровня производительности труда рабочего от его возраста. [c.329]
V Пример 6. Найти методом наименьших квадратов формулу параболической зависимости у от х [c.334]
Из рисунка 4.5.1 видно, что зависимость продаж от цены страховой продукции на интервале изменения 0,8-1,2 от ее среднего значения в первом приближении имеет параболический характер. Повышение или понижение цены на несколько процентов (до 4%) не приводит к существенному изменению количества продаж. В связи с этим интервал изменения цен в пределах 0,96-1,04 можно назвать зоной нечувствительности потребителей к изменению стоимости страховой продукции — неэластичности спроса по цене. В данной зоне страховщик может маневрировать ценами, не опасаясь потерять клиентуру, так как значительная часть потребителей не считает для себя существенным превышение цен на 1-4%. Потребительская оценка премии при ее изменении в этих пределах практически постоянная. Здесь можно применить аналогию из повседневной жизни в кармане у каждого человека есть мелочь, которой легко пожертвовать — пренебрежимо малая сумма. Прирост или уменьшение средств на эту сумму не является заметным и большая доля населения не будет прикладывать усилий, чтобы заработать ее. Точно так же и в страховании незначительное изменение стоимости полиса не является значимым для потребителя и не может компенсировать материальных и моральных затрат, связанных с переходом в другую компанию. [c.129]
Параболическая зависимость у = а0 + а +а21. Система нормальных уравнений для параболы имеет следующий вид [c.54]
При игре на повышение ставьте стоп-приказ ниже недавнего краткосрочного уровня поддержки, а при игре на понижение - выше недавнего краткосрочного уровня сопротивления (см. раздел 20). Параболическая система (см. раздел 44) перемещает стоп-приказы в направлении сделки в зависимости от [c.287]
Пр и мер 6.1. На рис. 6.1 представлены 63 результата специального эксперимента [50, с. 57]. Расположение точек на рис. 6.1 не дает ответа на вопрос, описывать ли зависимость между скоростью автомобиля (х миль/ч) и расстоянием (у футов), пройденным им после поданного сигнала об остановке, линейной или параболической зависимостью. [c.177]
| Рис. 10.1. Зависимость погрешности локальной параболической аппроксимации от величины b для выборки объема а) п = 75 б) л = | 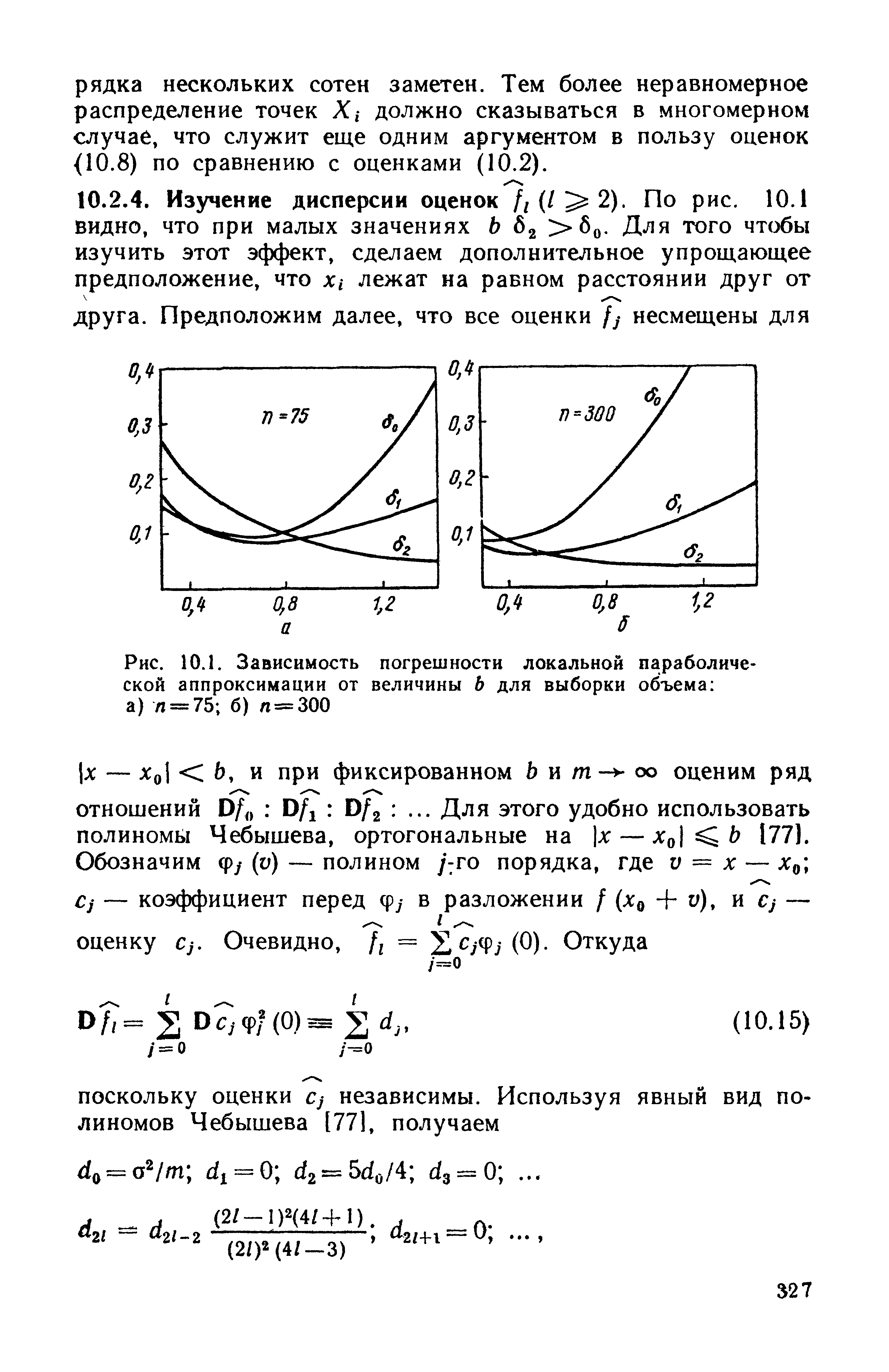 |
Оптимизация структуры капитала основывается на том, что цены собственного (С) и заемного капитала (3) не постоянны и увеличиваются при увеличении доли в общем капитале предприятия нелинейным образом. По данным [11], зависимость цены собственного и заемного капитала от их доли в общем капитале можно аппроксимировать параболической зависимостью с коэффициентами, определяемыми для конкретного предприятия методами корреляционного и регрессионного анализа. [c.318]
Таким образом, на данном отрезке графика зависимость У =/(3) имеет параболический характер. [c.189]
Данной задаче уделено много внимания в работах зарубежных и отечественных специалистов. Так, в ряде изданий приводятся графики для отдельных составляющих и обобщенных логистических издержек от количества складов (рис. 11.3). Считается, что транспортные затраты и упущенная выгода от продаж уменьшаются с увеличением количества складов, тогда как расходы на содержание запасов, эксплуатацию складского хозяйства и управление складской системой возрастают. Наличие указанных противоречивых тенденций приводит к тому, что зависимость общих затрат на функционирование системы распределения от количества складов имеет параболический характер с явно выраженным оптимумом. К сожалению, отсутствие соответствующих формул и количественных характеристик не позволяет проводить необходимые расчеты, т. е. вышеуказанные зависимости имеют качественный характер, основанный на логике и здравом смысле. [c.397]
Оценки коэффициентов параболической зависимости для тренда [c.173]
Прогноз с использованием экспоненциального сглаживания. Прогноз осуществляется по линейным и параболическим зависимостям. Параметры моделей рассчитываются по формулам, предложенным Брауном. Выбор параметра сглаживания ос производится в пределах от 0,1 до 0,9 с шагом 0,1. При комбинированном прогнозе выбор параметра производится по формуле а = 2/(N +1), где N - число точек временного ряда. [c.186]
Многие модели управляемых систем основаны на аппарате дифференциальных уравнений как в обыкновенных, так и в частных производных. При исследовании систем с распределенными параметрами, в зависимости от вида используемых дифференциальных уравнений в частных производных, выделяют такие типы задач оптимального управления, как параболические, эллиптические или гиперболические. [c.199]
Если полученные величины подставить в общую формулу целой рациональной функции, то мы получим интерполяционную формулу в виде параболической зависимости второго порядка, имеющую следующие коэффициенты при х [c.39]
На первый взгляд кажется странным, что с увеличением парка машин увеличивается численность рабочих, или внедрение 1 тыс. т сборных бетонных и железобетонных конструкций требует увеличения численности рабочих, При более внимательном рассмотрении этого вопроса можно сказать, что при увеличении парка машин, объема сборных конструкций увеличивается программа выполняемых работ, причем это увеличение идет более высокими темпами, чем возрастает численность рабочих, и, таким образом, трудоемкость работ на единицу продукции снижается. В то же время, определяя форму связи между переменными (линейная, обратная, параболическая) и используя при этом абсолютные цифры (объем работ, численность рабочих), мы в большинстве случаев получаем линейную зависимость, при которой упрощаются все вычисления. [c.147]
На практике чаще всего используются линейная, степенная и параболические зависимости экономических показателей от параметров изделий. [c.130]
В частности, параболическая зависимость между показателями имеет вид [c.131]
Исследование взаимосвязи между уровнем относительной приростной фондоотдачи и изменением соотношения темпов прироста труда и основных фондов показало существование между ними зависимости параболического характера (см. рис. 1). Зависимость была рассчитана в двух вариантах применительно к показателю относительной приростной фондоотдачи и к его модификации, образующейся после вычитания из величин погодо-вых темпов прироста конечного общественного продукта фиксированной средней величины ежегодного относительного прироста конечного общественного продукта за счет интенсивных факторов (X). В расчетах использовалась оценка параметра К, полученная из анализа производственной [c.42]
Нельзя согласиться с первым мнением Ф. Миллса, так как плавный уровень изучаемых динамических рядов может быть различен в зависимости от характера данного явления. Он может быть линейным, параболическим, гиперболическим и т. д. Мы предпочитаем точку зрения Н. К. Дружинина [40]. Исключая уровни динамических рядов, коррелируем отклонения от них. При этом не имеет значения, выражается ли этот уровень прямой или параболой. Отклонения от уровней временных рядов, независимо от их формы, являются беспорядочными числами, к которым можно применять корреляционно-регрессионный анализ. [c.73]
С помощью пакета можно находить не только линейные, параболические и гиперболические, но и любые другие аналитические зависимости (экспоненциальные, логарифмические, степенные и т. п.). Нужно лишь после команды least square поставить соответствующую формулу. [c.335]
Особый интерес для управления качествами страховой продукции представляет поведение зависимости продаж от цены в области изменения стоимости более 1,2 от среднерыночного значения. Здесь характер зависимости отклоняется от параболического, что объясняется различной чувствительностью к цене. Порядка 4% страхователей высоко чувствительны к стоимости услуг и легко меняют компанию в поисках более дешевых предложений того же качества. В соотношении цена-качество они делают акцент на стоимость услуги. 65-70% от общего числа потребителей относятся к средней категории чувствительности, которая соответствует более или менее равновесной оценке значимости цены и качества продукта. Оставшиеся 30-35% страхователей можно отнести к категории мало чувствительных к цене и более чувствительных к прочим (неценовым) качествам страховой услуги. Примером последней категории страхователей является традиционная клиентура Госстраха, приверженная данной марке, иногда вопреки здравому смыслу. Вообще чувствительность к цене определяется психологической ориентацией страхователей. Клиенты, настроенные на активное личное потребление (получение выгод), гиперчувствительны к цене. Они не только ищут наиболее дешевые предложения, иногда в ущерб качеству услуги, но и пытаются использовать все возможности для получения от компании максимального страхового возмещения и тогда, когда для этого нет никаких оснований. Те, кто склонен к поиску компромисса между своими интересами и интересами страховщика, менее чувствителен к стоимости полиса. [c.130]
Следует, однако, предупредить, что в этом случае, при сколь угодно гладкой зависимости /(х), операция проектирования Р% может привести к тому, что суперпозиция / (Pj) окажется уже негладкой. Такая ситуация показана на рис. 71, где изменение точки z (s)=Px (х—s/J, а следовательно, и / [z (s)], содержит изломы . В этом случае естественнее решать задачу определения s алгоритмом 46. Параболическая интерполяция может оказаться несходящейся. [c.398]
Названа по имени американского экономиста французского происхождения профессора Артура Лаффера — сторонника теории предложения, который доказывал, что более низкие ставки налогов вполне совместимы с прежними и даже возросшими налоговыми поступлениями. Лаффэр построил количественную зависимость между прогрессивностью налогообложения и доходами бюджета в виде параболической кривой и пытался доказать, что по мере роста ставки налога от О до 100% налоговые поступления будут расти до некоторого максимального уровня, затем этот рост немного замедляется и далее идет либо такое же плавное снижение налоговых поступлений, а соответственно и доходов бюджета, либо наблюдается их резкое падение. Налоговые поступления падают после некоторой точки потому, что более высокие налоговые ставки, по предположению Лаффэра, сдерживают экономическую активность и, следовательно, налоговая база сокращается. Например, 100%-ная налоговая ставка имеет характер конфискации и останавливает производство налоговая база становится равной 0 и приносит нулевой налоговый доход. Если успешное функционирование рынка будет сталкиваться с усиливающейся дискриминацией в виде более высоких и прогрессивных налогов... то экономическая активность будет падать , — отмечал Лаффэр. Предельной ставкой для налогового изъятия в бюджет является, по оценкам Лаффэра, 30% суммы доходов 40—50-процентное изъятие доходов сокращает сбережения населения, влечет за собой незаинтересованность в инвестировании в те или иные отрасли экономики и, следовательно, означает сокращение налоговых поступлений. [c.40]
Помимо представления тенденции в виде прямой линии, в М. с. используются и различные кривые. Среди них надо отметить, наряду с параболами второго, третьего, реже высших порядков (причём и в этом случае параметры соответствующих целых рациональных функций находятся обычно способом наименьших квадратов) показательные функции, к-рые получают, применяя параболическое выравнивание к логарифму рассматриваемой величины. В надлежащих случаях используются тригонометрич. функции и их ряды. Установление величины периода или сочетающихся периодов производится при этом с помощью пориодограмманализа — путём отбора периодов, дающих наибольшую амплитуду колебаний. В исследовании динамики М. с. всё чаще опирается на теорию случайных процессов в целом. В частности, получили развитие применение автокорреляционных функций (выражающих корреляционную зависимость данного значения от неск. предшествующих ему), спектральный анализ и др. приёмы. [c.400]
Профессор А. Лэффер выявил количественную зависимость между прогрессивностью налогообложения и доходами бюджета, представил ее в виде параболической кривой (рис. 1.1) и сделал вывод о том, что снижение налогов благоприятно воздействует на инвестиционную активность частного сектора. Во второй половине XX века кривая Лэффера получила всеобщее признание. Анализ кривой показывает, что чем выше налоговые ставки, тем более сильный побудительный мотив будет у индивидуумов для уклонения от налогов. Если предприниматель не видит перспективы получения прибыли или если успешное функционирование рынка сопровождается прогрессивным налогообложением, то экономическая активность падает. Заинтересованность хозяйствующих субъектов является движущей силой процветающей экономики. [c.14]
