| Рис. 2.З. Оптимальное f в качестве горизонтальной асимптоты. | 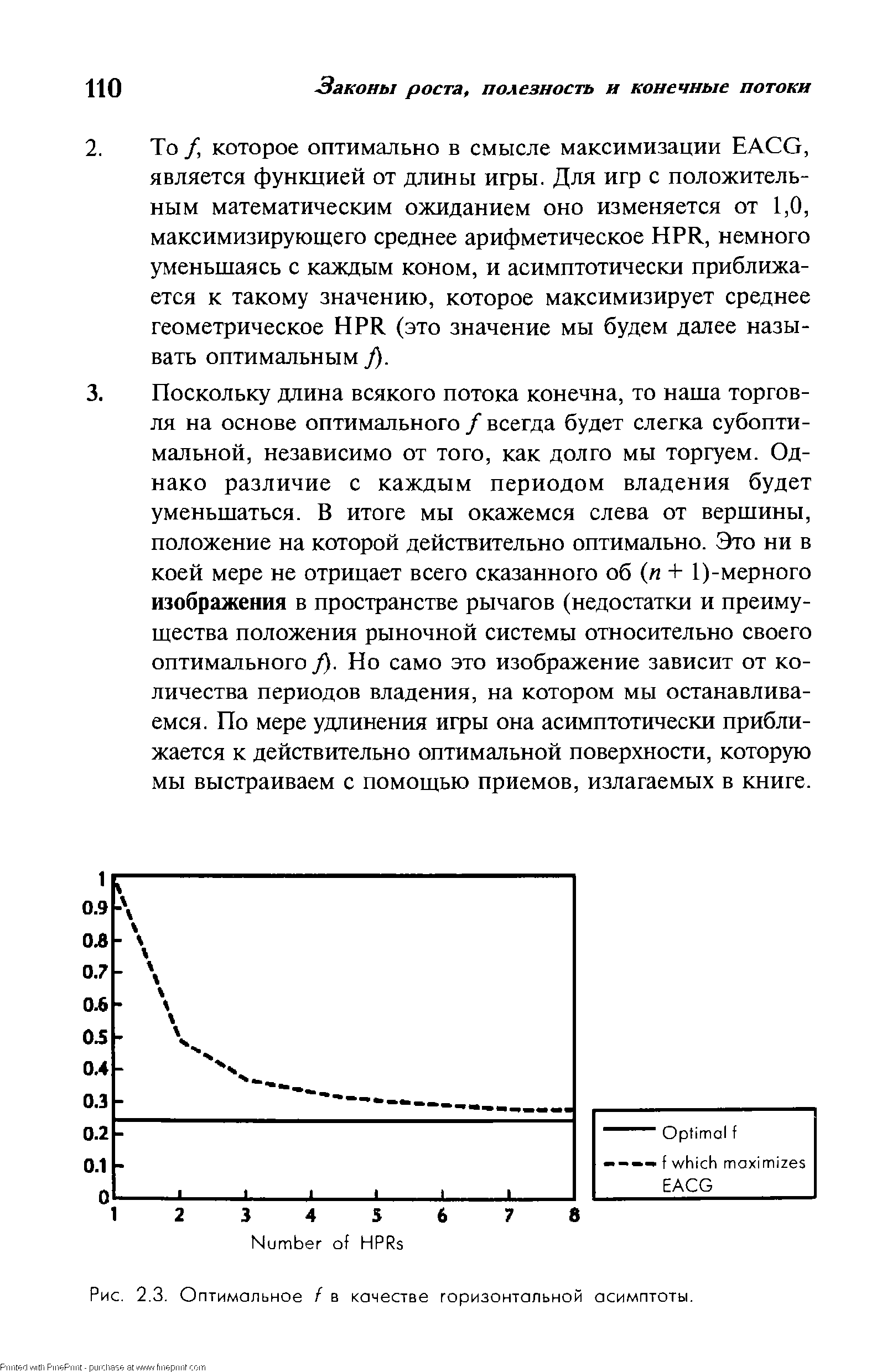 |
Горизонтальные асимптоты. График функции у = f(x) при х —ь +оо или х —> — оо имеет горизонтальную асимптоту, если существует и конечен хотя бы один из пределов [c.167]
Если конечен предел 6Л, то говорят, что существует левосторонняя горизонтальная асимптота у — 6Л. [c.167]
В случае, когда конечные пределы 6Л и 6П совпадают 6Л = 6П, говорят, что график функции у = /(ж) имеет двустороннюю горизонтальную асимптоту у = Ь. Примеры двусторонних горизонтальных асимптот приведены на рис. 9.21. [c.167]
| Рис. 9.21. Двусторонние горизонтальные асимптоты | 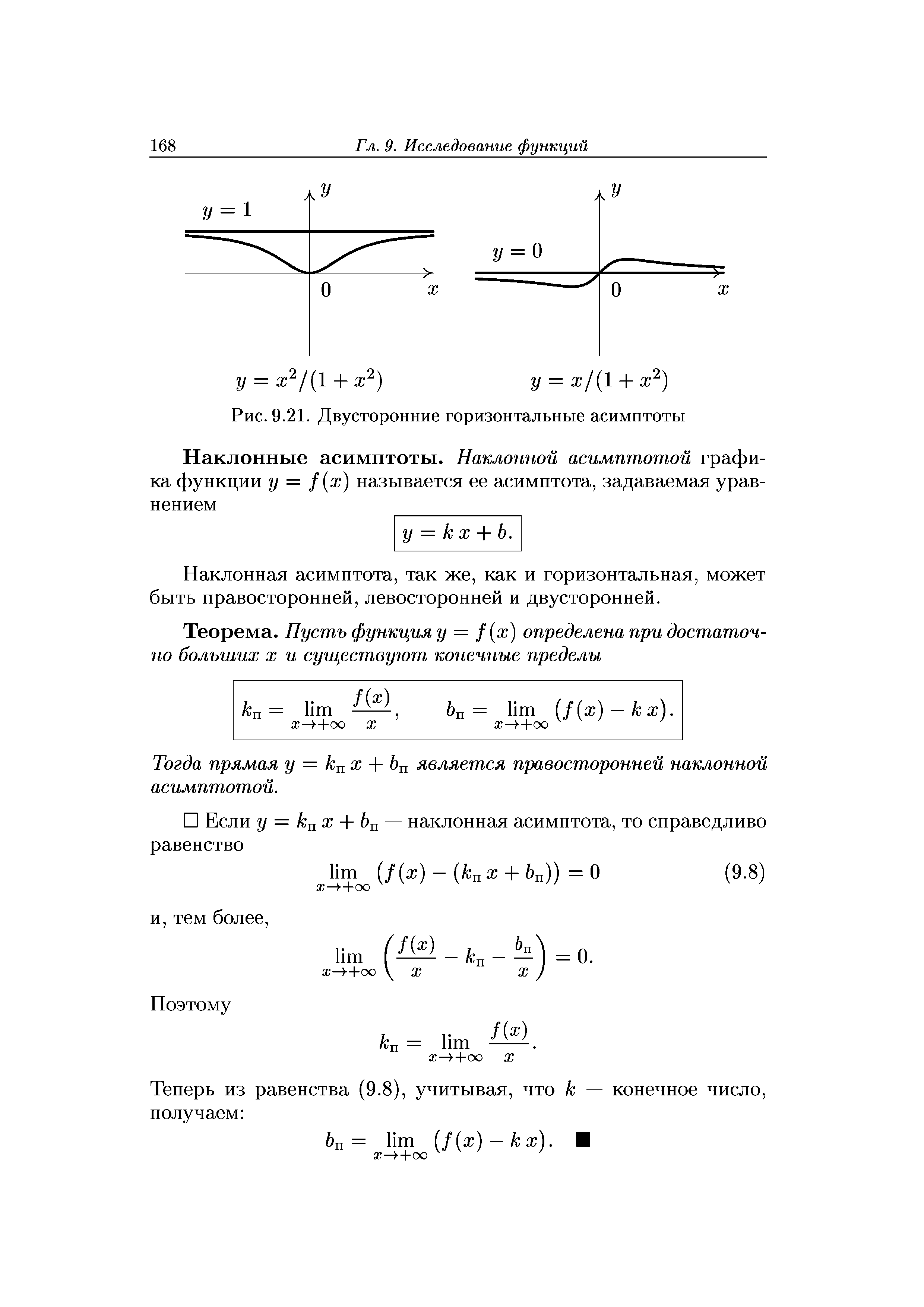 |
Горизонтальную асимптоту можно рассматривать как частный случай наклонной асимптоты при k = 0. Поэтому при отыскании асимптот рассматривают лишь два случая 1) вертикальные асимптоты 2) наклонные асимптоты. [c.170]
Если оба предела существуют и конечны, то прямая у = ku х + 6П является правосторонней наклонной асимптотой (правосторонней горизонтальной асимптотой, если k = 0). В противном случае правосторонних наклонных и горизонтальных асимптот не существует. [c.170]
Левосторонние наклонные (горизонтальные) асимптоты находятся аналогично. [c.170]
Следовательно, кривая имеет вертикальную асимптоту х = 1. 2) Найдем наклонные и горизонтальные асимптоты (если они есть). Для этого вычислим соответствующие пределы [c.171]
Найдем наклонные и горизонтальные асимптоты (если они есть). Для этого вычислим соответствующие пределы [c.171]
Таким образом, л = п = оо. Следовательно, график функции не имеет также наклонных асимптот и горизонтальных асимптот (если бы горизонтальная асимптота существовала имели бы k = 0). [c.173]
Итак, график функции не имеет асимптот ни вертикальных, ни наклонных, ни горизонтальных. А [c.173]
Ответ График функции у = ж2 не имеет асимптот. Графики функций у = ж2/(1 + ж2) и у = ж/(1 + ж2) имеют двусторонние горизонтальные асимптоты, которые изображены на рис. 9.21. (Асимптотой графика функции у = ж /(1 + ж ) является прямая у = 1, а асимптотой графика функции у = ж/(1 + ж2) является ось абсцисс.) [c.173]
Так как функция является непрерывной, то ее график не имеет вертикальных асимптот. Наклонных и горизонтальных [c.175]
Этот тип кривых (рис. 6.3) характеризуется двумя асимптотами (прямыми, к которым график функции неограниченно приближается, не достигая их) горизонтальной у = а и вертикальной х = 0, а также параметром искривления Ь. С помощью преобразования независимой переменной х = l/х (т. е. перехода к новому аргументу) эта зависимость приводится к линейному виду у = а + Ьх [c.185]
Рассматриваемые кривые (рис. 6.5) имеют горизонтальную асимптоту у = На, вертикальную асимптоту х — — Ыа и характеристику искривления, равную — b/а 2. С помощью [c.186]
Кривые (рис. 6.6) проходят через точку (0,Л), причем ось х является их горизонтальной асимптотой. Если вместо т] (соответственно y j) в качестве зависимой переменной рассмотреть величину т] = In ц (соответственно / = In то данная зависимость преобразуется к линейному виду — а + Ьх, в котором а == In A [c.187]
При b > 0 кривая (рис. 6.7, а) имеет горизонтальную асимптоту у = А и вертикальную асимптоту х = 0. При Ь < О [c.187]
Частный случай так называемой логистической кривой показан на рис. 6.8. Кривая имеет две горизонтальные асимптоты у = 0 и у = На и точку перегиба (In ( /a ), 1/2я). Линеаризация этой зависимости производится с помощью перехода к новым переменным т] = 1/т (соответственно yt = и А = ег . [c.188]
Функции потерь, имеющие горизонтальную асимптоту. Предложены три семейства функций, специально рассчитанных на асимметричные отклонения функции распределения ошибок от нормального закона. В унифицированных обозначениях в условиях, когда дисперсия основной (незасоренной) части распределения регрессионных остатков известна и равна единице, они могут быть приведены к виду (ниже параметр К > 0) [c.216]
Все три функции при Я- > О стремятся к и2/2, т. е. переходят в обычную квадратичную функцию потерь, используемую в мнк. При Я Ф О они имеют горизонтальную асимптоту, равную К . Взаимное расположение этих функций для двух значений параметров показано на рис. 7.1. [c.216]
В классических предположениях мнк-оценки совпадают с оценками максимального правдоподобия и являются наилучшими среди всех несмещенных оценок в. Однако при отклонении распределения г от нормального в сторону увеличения вероятности больших отклонений мнк-оценки быстро теряют свои оптимальные свойства. В связи с этим в практической работе широко используются функции потерь р(и) Ф и2. Среди них выделяется функция ря, (и) = А,-1 (1 — ехр — А,м2/2 ), при К -> 0 стремящаяся к и2/2, а при и - оо (X > 0) имеющая горизонтальную асимптоту. Она приводит к так называемым эв-оценкам параметров регрессионной зависимости (эв-регрессия или Х-регрессия). Эти оценки устойчивы к нарушению предположения нормаль- [c.249]
Асимптоты. Асимптотой графика функции называется прямая, к которой сколь угодно близко приближается график данной функции при стремлении аргумента к бесконечности или к некоторому числу а или случай вертикальной асимптоты. Асимптоты могут быть вертикальными, горизонтальными и наклонными. [c.25]
Горизонтальная асимптота - это прямая у = Ь, если х Наклонная асимптота - это прямая у = kx + b, если 1ш1(Дх) - kx) = Ъ. Коэффициент наклона k находится путем вычис- [c.25]
Областью определения функций является объединение интервалов (-оо, 0) и (О, +QO), а областью значений - множество (0,+оо). Функции четные. Ветви функций расположены в первой и четвертой четвертях (см. рис.8а) Оси координат являются вертикальной и горизонтальной асимптотами. [c.30]
Дайте определение асимптоты. Приведите пример функции, имеющей горизонтальную асимптоту. Приведите пример функции, имеющей вертикальную асимптоту. [c.41]
Определение. Асимптота, определяемая уравнением у = Ь, называется горизонтальной асимптотой. [c.68]
Исследовав стандартным методом функцию fl3)(f), найдем, что она определена на (0, +°°), не является ни четной, ни нечетной и ни периодической, возрастает на промежутке (0, 2/3) и убывает на промежутке (2/3, -н ) точка 2=2/3 является точкой максимума, а сам максимум равен тах/(3)(0 =0,784 точки ,=(2-V2)/3 и t, = (2+V2)/3 являются точками перегиба графика этой функции, ] /(3)(0=1 Хз)(0=0, т.е. ось Ot является для графика функции 7<з>(0 горизонтальной асимптотой. На основании полученных данных построим график функции fl3)(f), который имеет следующий вид (см. рис. 7.5). [c.118]
Таким образом, при ж — > +оо асимптотой слулсит прямая у = 1 (правосторонняя горизонтальные асимптота), а при ж — > — оо — [c.172]
Переход к производственным функциям с семейством монотонных линий уровня f (k, I) — onst, имеющих горизонтальные и вертикальные асимптоты и конечные пределы вида lim / (k, 10) = F (/0) и lim f (k0t. [c.46]
Это опрсдетенпе относ 1гя как к наклонной, т к и к шризопталыюй асимптотам- в случае горизонтальной асимптоты угловой коэффициент ft и (6 11) равен нулю, [c.119]
I ертикальн я асимптота, у = 3 горизонтальная асимптота. 6.22. у 0 горизонтальная асимптота. 6.23. у х 1 л клонная асимптота, я I — вертикальная асимптота [c.437]
