После того, как задача сформулирована в терминах линейного программирования, решение ее состоит в применении того или иного расчетного алгоритма. Наиболее распространенными методами решения задач линейного программирования являются симплексный (или метод последовательного улучшения плана), распределительный и индексный. Существует также ряд приближенных методов решения, разработанных для отдельных видов задач (пример решения задачи методом линейного программирования дан ниже). [c.153]
В современных условиях наиболее приемлемой формой для повышения загрузки персонала является совмещение профессий. Например, на газопроводах и ПХГ можно совмещать профессии слесарей и машинистов. В соответствии с постановлением ЦК КПСС и Совета Министров СССР Об улучшении плани- [c.120]
Можно сформулировать и другие показатели. Интересно отметить, что хотя для большинства показателей направление их улучшения очевидно (так, производство естественно стараться увеличить, а потребление воды и удобрений — уменьшить), для некоторых показателей направление изменения, приводящее к улучшению плана, зависит от конкретной ситуации. Например, показатель занятости трудящихся в производстве /4 стремятся либо уменьшать, либо увеличивать в зависимости от того, есть ли воз- [c.174]
Таким образом, ясно, что для уменьшения значения критерия необходимо уменьшить потенциалы в пунктах-потребителях. На этом соображении и основывается алгоритм улучшения плана. Заметим, что введение новой ненулевой поставки между соседними пунктами, соединенными неиспользуемой дорогой, позволяет изменить потенциалы. Конечно, нужно ввести в план такую поставку, которая приведет к уменьшению потенциалов. Для того чтобы оценить, к каким последствиям приведет введение новых поставок, сравним удельные затраты для всех неиспользуемых дорог с разностью потенциалов в связываемых ими пунктах. Точнее говоря, подсчитаем характеристики неиспользуемых дорог, [c.190]
Для улучшения плана имеет смысл перемещать перевозки только по тем циклам, цена которых отрицательна. Поскольку по условию (74) перевозки не могут быть отрицательными, то для улучшения плана используют только такие циклы, вершины которых, отмеченные знаком минус (—), находятся в базисных клетках транспортной таблицы. [c.74]
В начале первой итерации улучшения плана все ритмы равны своим минимальным значениям, поэтому множитель" выбирается из условия (60). Для его определения рассчитываем для всех j [c.76]
Как уже было показано, ув = 5Ч . Итак, получено существенное сокращение целевой функции, однако критерий 56 продолжает оставаться положительным, что говорит о необходимости дальнейшего улучшения плана [c.71]
Таким образом, мы получили следующие значения переменных для второго, улучшенного плана [c.77]
После улучшения плана стоимость брака Ду уменьшилась на следующую величину [c.82]
Дальнейшее улучшение плана выполняется аналогичным путем. Улучшенные планы сведены в таблицы. Четвертый - в табл. 3.12 пятый-в табл. 3.13 шестой-в табл. 3.14. [c.86]
| Таблица 4.5 Второй вариант улучшения плана | 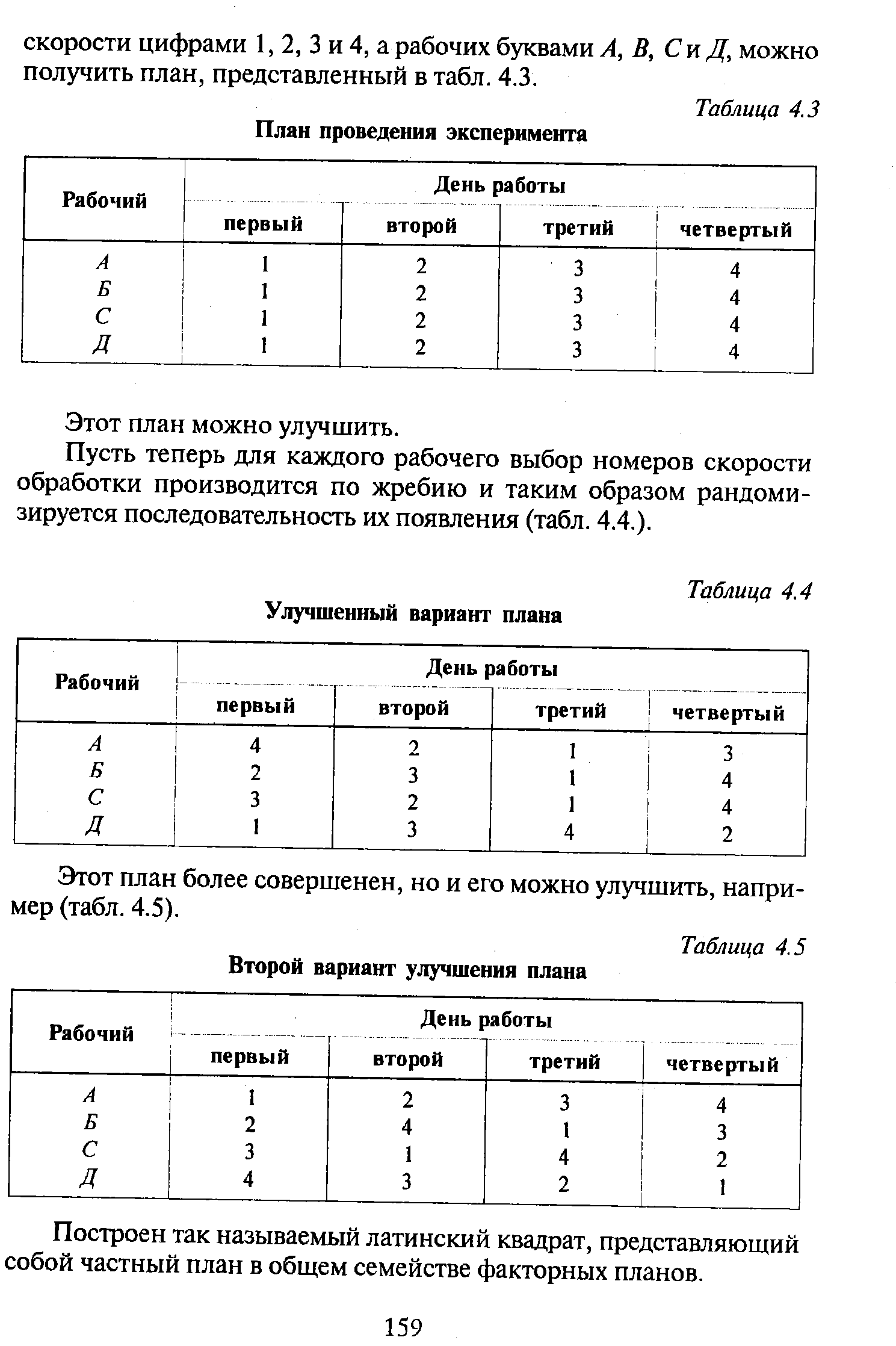 |
Алгоритмы, применяемые при этом (итеративные алгоритмы методов последовательного улучшения плана), можно разделить на три класса [c.137]
Итеративные алгоритмы методов последовательного улучшения плана 137 [c.468]
Этап 6. Анализ разработанного варианта плана. Решает ли разработанный план поставленные на этапе 1 задачи Являются ли затраты ресурсов приемлемыми Есть ли соображения по улучшению плана, возникшие в ходе его разработки при движении от этапа 2 к этапу 5 Возможно, целесообразно вернуться к этапу 2 или 3, или даже к этапу 1. [c.140]
В результате проведения конечного числа шагов улучшения плана выявляются следующие вопросы [c.145]
Решение транспортных задач включает разработку отправного варианта распределения имеющихся у поставщиков запасов (мощностей) между потребителями с учетом их потребностей (спроса) и выполнение нескольких итераций исходного плана. Каждая из итераций состоит из проверки полученного плана на оптимальность и улучшения плана, если последний оказался не оптимальным. Получение исходного плана. Для первоначального распределения используются способы северо-западного угла, наименьшего (наибольшего) элемента по строке, наименьшего (наибольшего) элемента по столбцу, наименьшего (наибольшего) элемента матрицы. [c.139]
Таким образом, в плане (табл. 22.19) все свободные клетки имеют положительные характеристики. Это свидетельствует о том, что дальнейшее улучшение плана невозможно, и полученный вариант является оптимальным. Затраты на доставку сырья по оптимальному плану составляют 430 тыс. руб. [c.147]
Совокупность методов, интенсифицирующих процесс разработки и качественного улучшения плана, образует методологическую основу интегрированной системы планирования. В нее вошли программированный расчетно-анали-тический метод, методы инициативного и напряженного планирования. [c.20]
Ко второй ступени преобразования плановой информации после завершения разработки базового варианта годового плана подключаются процедуры улучшения плана (рис. 5, блок 5). [c.28]
Следует отметить социальный анализ весьма сложен — прежде всего, по причине затруднительности применения формальных методов и отсутствия стандартных методик и процедур. Вместе с тем, успешное его проведение способствует улучшению плана проекта, а также эффективности проекта в целом. [c.84]
Составление начального варианта прикрепления. При решении транспортной задачи на матрице путем последовательного улучшения плана начальный вариант прикрепления может быть составлен несколькими способами, два из них следующие. [c.141]
В 1940 г. эксплоатационные тонно-километры превышали тарифные на 4,6%, а в 1945 г. на 8,0%. За последние годы в результате увеличения провозной способности кратчайших направлений, улучшения плана формирования поездов, усиления контроля за правильностью заполнения маршрутов машинистов и улучшения действующей отчётности этот разрыв уменьшился и составил в 1953 г. менее 2%. [c.46]
За прошедшие годы существенно развилась вычислительная техника. Внедрение электронно-вычислительных машин выдвинуло теперь на первый план вопросы автоматизации решения задач о рациональном раскрое. В первом издании эти вопросы освещались с учетом вычислительных возможностей тех лет, хотя необходимые алгоритмы для разработки машинных вычислительных программ уже содержались в книге. Отметим, в частности, метод последовательного улучшения плана раскроя, центральный для решения задач линейного программирования на ЭВМ, и метод построения шкалы индексов, по существу предвосхитивший метод рекуррентных соотношений динамического программирования. [c.3]
Отметим, что план № 8 явно неэкономный. Первый раскрой позволяет из отхода получить еще заготовку в 650 мм. Третий раскрой позволяет одну из заготовок увеличить до 950 мм. Поэтому мы сразу перейдем к улучшенному плану № 9. [c.39]
Индексы преобладающих заготовок. Пусть из общего списка заготовок несколько заготовок — преобладающие — нужны в значительно большем количестве, чем все остальные. Допустим мысленно, что мы отдельно раскроим только преобладающие заготовки и определим их индексы и отдельно раскроим остальные заготовки и тоже определим их индексы, а затем разрешим применение смешанных раскроев и будем изменять план по общему методу последовательных улучшений плана раскроя ( 4 гл. I). [c.104]
Так как задача раскроя рулонного материала, по существу, сводится к основным задачам 1 и 2 ( 3 гл. I), то к этой задаче могут быть применены общие методы, изложенные в гл. I . Например, общий метод последовательных улучшений плана раскроя принимает в случае рулонного материала следующий вид [c.138]
Если внутри некоторых крупных полос отходы велики, следует перейти к улучшению плана раскроя путем усложнения состава полос (методом, изложенным в начале этого параграфа). [c.148]
В распоряжении вычислительных центров, как правило, имеются стандартные программы для решения на ЭВМ задач линейного программирования. По существу большинство из них реализует методы, эквивалентные описанному в этой книге методу последовательного улучшения плана. В зарубежной литературе он известен под названием модифицированного симплекс-метода. Упомянем публикации программ [c.222]
О поиске на ЭВМ оптимальных планов раскроя мерных линейных материалов и оптимальных планов раскроя прямоугольных листов на прямоугольные заготовки. Совершенствованием алгоритмов для решения задач раскроя без составления перечня раскроев — путем чередования шагов улучшения плана с поиском улучшающего раскроя методом динамического программирования — в последние годы занимались многие специалисты. [c.224]
Поскольку среди разностей ( j/ — с -) есть положительные, план (x j) также не является оптимальным и процесс улучшения плана должен быть продолжен. [c.263]
Решение транспортных задач методом потенциалов. Продемонстрируем метод решения транспортных задач в сетевой постановке, так называемый метод потенциалов. Он был предложен Л. В. Канторовичем в начале сороковых годов п является первым методом решения транспортных задач. Интересно отметить, что метод с самого начала предназначался для решения транспортных задач в сетевой постановке и только впоследствии был преобразован к матричной форме. Метод потенциалов является одним из способов реализации общего принципа решения задач линейного программирования — принципа последовательного улучшения плана, о котором мы уже говорили в 4 гл. 1. [c.189]
В базис z-задачи вводится вектор р , для которого соответствующий коэффициент линейной формы (9) равен <ть= (С, xv . ) Дальнейшее решение z-задачи проводится по правилам второго алгоритма метода последовательного улучшения плана. Таким образом, из приведенной схемы видно, что решение рассматриваемой задачи сводится к многократному решению однопродук-товых задач. [c.67]
ОПТИМИЗАЦИЯ НА СЕТЯХ [network optimization] в системах сетевого планирования и управления (СПУ) — улучшение плана, сформулированного сетевым графиком или заменяющим его алгоритмом анализа комплекса работ. Критериями оптимизации могут быть время завершения комплекса работ (выполнение плана в срок), минимум затрат на их выполнение и др. Как правило, временные и затратные критерии противоречат друг другу (форсирование работ требует дополнительных затрат), и потому одной из типичных задач исследования операций является выяснение того, какие дополнительные средства и в какие работы следует вложить, чтобы общее время выполнения комплекса работ было не больше заданной величины. Возможна и обратная постановка задачи до каких пределов можно увеличить время выполнения комплекса в целом (и отдельных работ), чтобы полученная экономия средств была максимальной. [c.247]
Как известно, на каждом шаге процесса решения в любом из методов линейного программирования выполняют следующие операции а) получают решение б) проверяют полученный план на оптимальность в) в случае неоптимальности выявляют тот вектор, который нужно ввести в базис (опорный план) улучшенного плана. В методе Данцига—Вулфа этот процесс распределяется между главной задачей, с одной стороны, и локальными задачами — с другой. [c.179]
На рис. 5 представлена структура ИСПТ информационно-преобразующий комплекс + блоки качественного улучшения плана. Классическая модель интегрированной системы обработки данных (в нашем случае данных планирования) дополняется процедурами анализа, корректировки, инициативного планирования, определения напряженности плана, оптимизации, текущего контроля и учета, оценки соответствия выполненного плана пятилетнему заданию на год (блоки 3, 5, 7, 9). Возможно, представленный набор процедур и приемов ИСПТ не является исчерпывающим. Но достижение режима функционирования ИСПТ, близкого к оптимальному, означает разработку плана активными методами, организацию текущего контроля выполнения и оценки конечных запланированных результатов. [c.25]
Работа в программированном режиме и в дисплейном варианте ускоряет разработку и формирование окончательного плана. Вторая ступень процесса планирования завершает сборку отдельных разделов годового плана в единое целое. В результате улучшения плана система достигает нового качественного состояния, близкого к финальному. На выходе второй ступени имеем последовательность А , А<>, . .., А которая означает, что первый, второй и все остальные разделы годового плана, включая сводный, достигли субфинального состояния (рис. 5, блок 6). Этому состоянию отвечают наилучшие экономические показатели плана. [c.28]
Последовательное развитие ИСПТ заключается прежде всего в дальнейшем совершенствовании активных методов обработки информации и качественном улучшении плана. Можно увеличить число активных приемов разработки плана, полнее использовать автоматизированное рабочее место, оборудованное в ПЭО, что скажется на увеличении уровня автоматизации и росте плодотворности плановой работы. Хорошо налаженные два остальных элемента ИСПТ — организационная структура и форма оплаты труда — служить будут долго, дополняя и стимулируя развитие активных методов планирования. [c.34]
Улучшение плана целесообразнее начинать с клетки с максимальной величиной нарушения (в примере с клетки RtPn)- [c.144]
Порядок действий для улучшения плана. Из выбранной клетки Я4Р8 с нарушением условия оптимальности проводим замкнутую ломаную линию, заканчивающуюся в той же клетке. Направление движения ломаной линии меняется под прямым углом и только в занятых клетках. J44 [c.144]
Приведенные примеры показывают, однако, лишь возможность перемещения значений переменных по клеткам таблицы без нарушения требований допустимости . Но такое перемещение имеет смысл только в том случае, если оно дает улучшение плана, в данном случае — снижение общего пробега грузов. Поэтому процедура Р. м. л. п. заключается прежде всего в проверке всех свободных клеток по кольцам возможных перемещений с точки зрения результативности этих перемещений, возможности за счет них улучшить результат. Проверка основывается на оценке этих колец по алгебраич. сумме пробегов по клеткам, через к-рые проходит это кольцо , учитывая показанные в схеме рис. 1 и 2 знаки + и — . Так, в приведенном на рис. 1 кольце оценки располагаются след, образом (см. данные о пробегах для каж-. — — дои клетки в табл. 2). В итоге получаем +3 + 3 — 1—2 = 3 следовательно, перемещение загрузки по кольцу рис. 1 в свободную клетку 13 за счет клеток 12 и 23 нецелесообразно общий пробег грузов при таком изменении плана перевозок увеличится по сравнению с исходным вариантом на 3 км по каждой единице груза, переносимой в клетку 13. [c.406]
При анализе плана по кольцам возможных перемещений проверяются все свободные клетки, для каждой из к-рых вычисляется сравнительная эффективность ее использования для улучшения плана. После этого производят перераспределение значений переменных по клеткам таблицы, новый план подвергают такому же анализу по вновь образовавшимся кольцам , и эту про-ЦОДУРУ повторяют до тех пор, пока все кольца будут давать отрицательный результат, чем будет доказана невозможность дальнейшего улучшения плана. Таким путем и будет достигнут оптимальный вариант плана. [c.406]
С. Каримбердиева. Метод последовательного улучшения плана.— Тр. по вычисл. матем. и технике. Работы молодых ученых. Ташкент, 1962. [c.222]
