Сколько же будет производить каждая фирма Кривая реакции каждой фирмы говорит о том, сколько она будет производить при том или ином предполагаемом объеме производства своего конкурента. При равновесии каждая фирма устанавливает объем производства в соответствии со своей собственной кривой реакции, и поэтому равновесный уровень объема производства находится на пересечении двух кривых реакции. Мы называем итоговое равновесие объемов производства равновесием Курно. При таком равновесии каждая фирма правильно предполагает, сколько будет производить ее конкурент, и в зависимости от этого может максимизировать прибыль. [c.349]
Тогда мы можем определить кривую реакции для фирмы 1 следующим образом. Чтобы максимизировать прибыль, фирма устанавливает предельный доход, равный предельным издержкам. Общий доход RI фирмы 1 дается как [c.351]
Кривая реакции фирмы 1 Q = 15 — /2Q2. (12.1) Такие же расчеты вы можете сделать для фирмы 2 [c.351]
Кривая реакции фирмы 2 Q2 = 15 — AQi- (12.2) 351 [c.351]
Равновесные уровни объема производства являются координатами Qi и Q2 точки пересечения двух кривых реакции, т. е. решениями уравнений (12.1) и (12.2). Заменяя Q2 в уравнении (12.1) выражением из правой части уравнения (12.2), мы можем утверждать, что равновесными объемами производства являются [c.352]
Рис. 12.5 показывает кривые реакции Курно и данное равновесие Курно. Отметим, что кривая реакции фирмы 1 показывает ее объем производства Qi в терминах объема производства фирмы 2 Q2. Аналогично кривая реакции фирмы 2 показывает Q2 в терминах Qi. Так как фирмы идентичны, две кривые реакции имеют одинаковую форму. Они выглядят по-разному, потому что одна дает Qi в терминах Qa, а другая дает Q2 в терминах Qi. Равновесие Курно находится на пересечении этих двух кривых. [c.352]
Кривая реакции фирмы 2 [c.352]
Объединив оба графика, получим кривые реакции обеих фирм на поведение друг друга. На рис. 12.9 кривая А1 отражает реакцию одноименной фирмы на изменения в производстве фирмы Y, а кривая Y — соответственно наоборот. Равновесие наступает в точке пересечения кривых реакций обеих фирм. В этой точке предположения фирм совпадают с их реальными действиями. [c.258]
| Рис. 12.9. Кривые реакции фирм Х и Уна поведение друг друга |  |
Задача определения реакции рынка на уровень сервиса не менее сложна, чем задача определения экономического эффекта от рекламных мероприятий. Кривая реакции рынка, как правило, имеет S-образную форму (рис. 64), что объясняется двумя основными причинами. [c.245]
После определенного уровня сервиса рынок становится нечувствителен к его дальнейшему увеличению. На кривой реакции рынка точка максимального порога сервиса указывает на уровень обслуживания, после которого увеличение сервиса не сопровождается увеличением продаж. [c.246]
Кривая реакции фирмы Л [c.51]
| Рис. 3. Кривые реакции обеих фирм и равновесие Курно. | 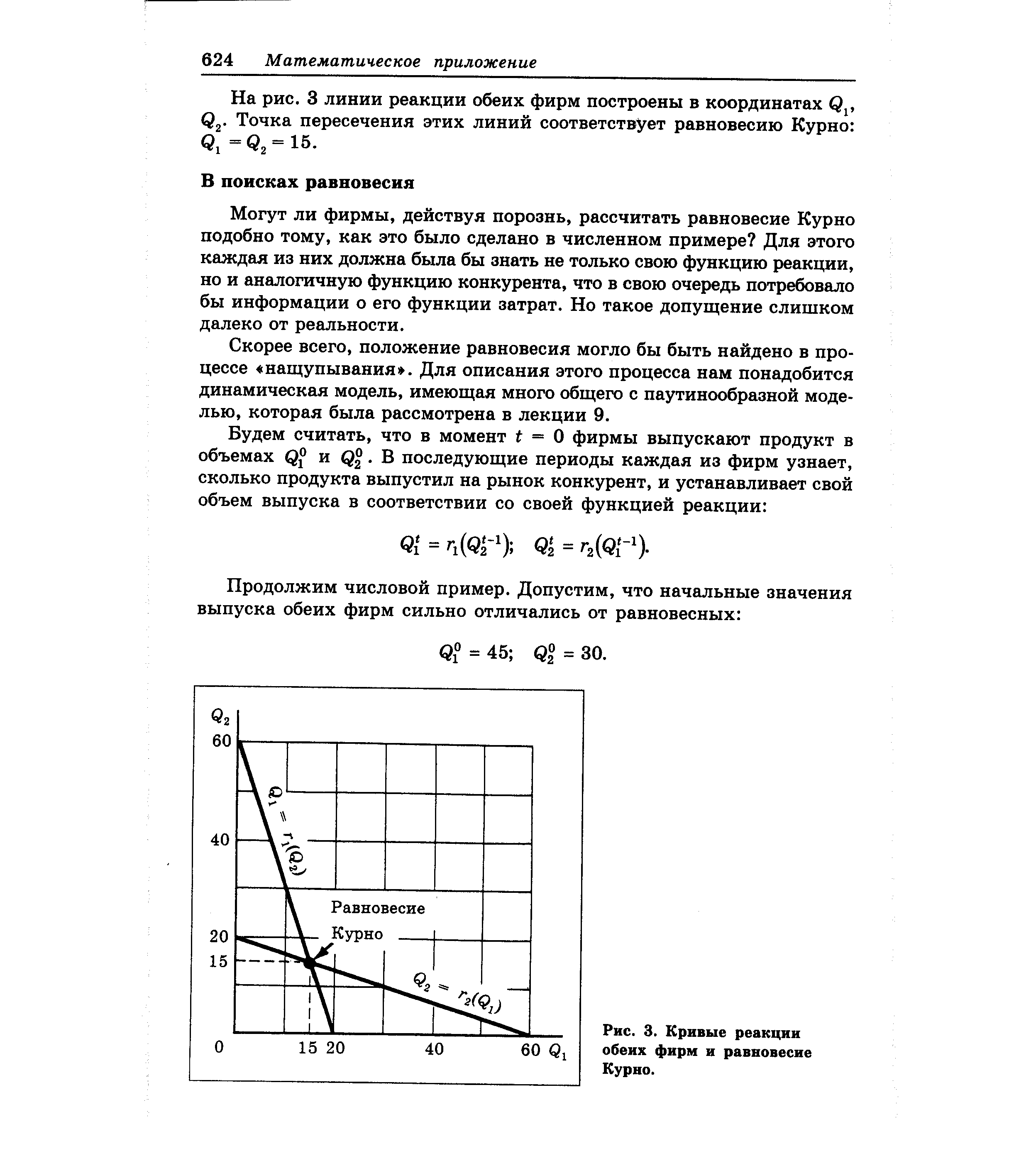 |
| Рис. 7.1. Модель Бертрана кривая реакции Фирмы 1 | 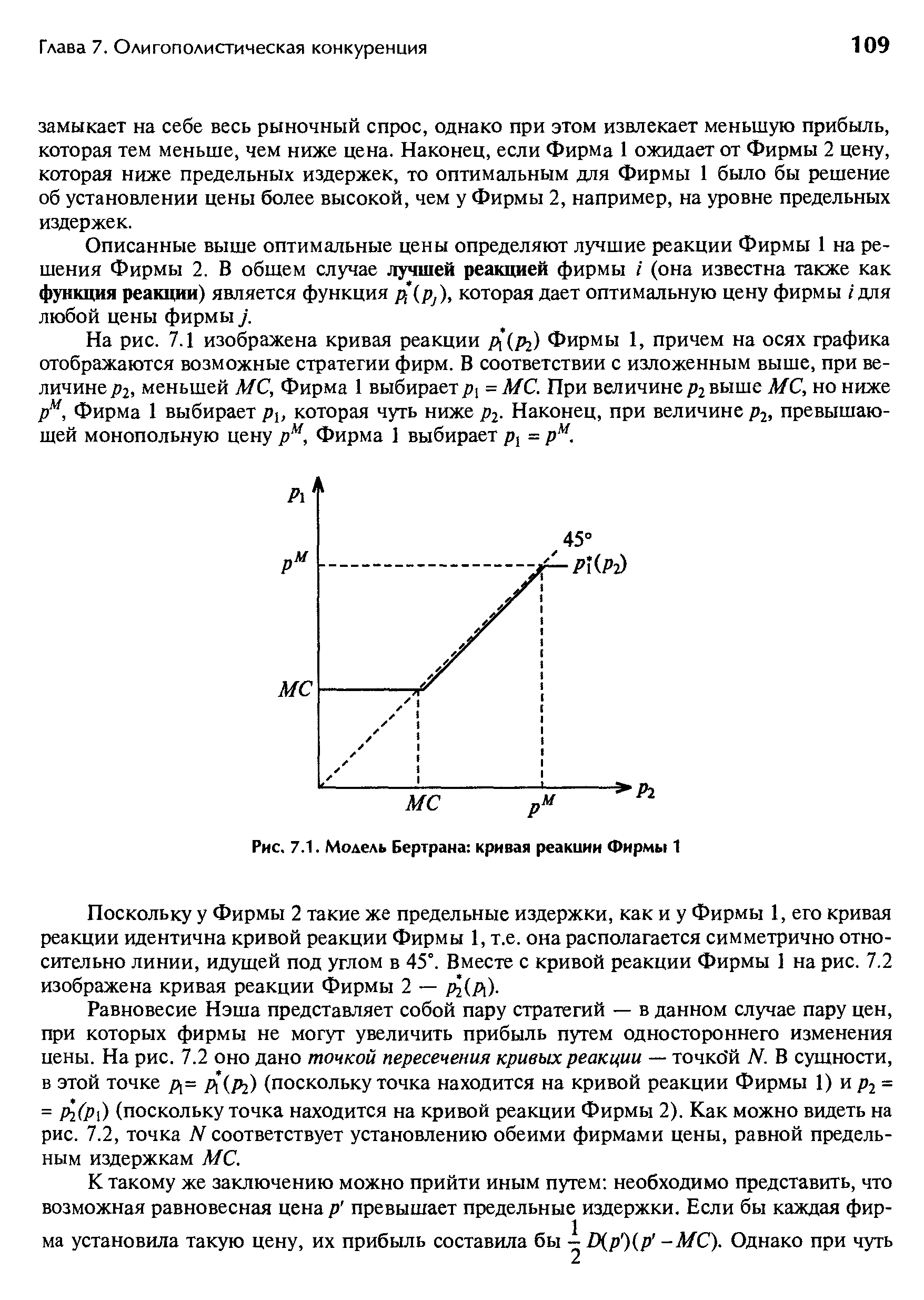 |
Как и в параграфе 7.1, нашей целью является вывод равновесия в модели, т.е. равновесия в игре, где участвуют две фирмы. Как и раньше, мы делаем это в два этапа. Во-первых, мы определяем оптимальный выбор каждой фирмы с учетом прогнозируемых им действий конкурента, т.е. кривую реакции фирмы. Во-вторых, совмещаем кривые реакции и находим комбинацию взаимно согласующихся действий и прогнозов. [c.114]
Точка равновесия в модели Курно задана пересечением кривых реакции, т.е. это точка N. В этой точке gl = д (д2) (поскольку точка лежит на кривой реакции Фирмы 1) и д2 = = q (q ) (поскольку точка лежит на кривой реакции Фирмы 2). [c.117]
Это можно проверить при помощи рис. 7.8, в основе которого лежит рис. 7.7 с добавлением нескольких дополнительных линий. Помните, что кривая реакции каждой фирмы пересекает оси в точках дм и q . Таким образом, линия с наклоном -1, пересекающая оси в наиболее удаленных крайних точках кривых реакции, соединяет все точки, при которых qf + д = q (см. рис. 7.8). Аналогично, линия с наклоном -1, пересекающая оси в ближайших крайних точках кривых реакции, соединяет все точки, при которых qf + q% = qM (см. рис. 7.8.). Очевидно, что точка равновесия Курно N лежит между этими двумя линиями. Значит, совокупный выпуск в модели Курно больше, чем при монополии, и меньше, чем при совершенной конкуренции. [c.118]
При рассмотрении графического вывода равновесия Курно мы видим, что функция реакции каждой фирмы зависит от ее предельных издержек . Таким образом, нам необходимо рассчитать новую кривую реакции, учитывая возросшие предельные издержки. На рис. 7.9 мы определили две крайние точки на кривой реакции новое значение (0) (т.е. qM) и новую величину q , причем q (q ) = 0. Опираясь на эти точки, мы можем прочертить новую кривую реакции, что и сделано на рис. 7.10. [c.121]
Рнс. 7.10. Смешение кривой реакции Фирмы 1 [c.121]
Увеличение предельных издержек смещает кривую реакции вниз. [c.121]
Это весьма важное обстоятельство, и мы его еще не раз встретим в самых разных видах. Благодаря симметрии, нам известно, что у обеих фирм произойдет смещение кривой реакции на одно и то же расстояние. Таким образом, у нас есть все необходимое, чтобы определить новое состояние равновесия. Оно отражено на рис. 7.11 и обозначено точкой N". Для сравнения на рисунке есть точка N, обозначающая предыдущее состояние равновесия. Как и ожидалось, объем производства каждой фирмы, так же как и совокупный объем производства, меньше в условиях нового состояния равновесия отсюда вывод, что цена выше. [c.121]
В рассмотренном выше примере мы видели, что увеличение предельных издержек означает смещение кривой реакции вниз. По аналогии резонно предположить, что в результате снижения предельных издержек (в долларах США) кривая реакции японской фирмы смещается вверх. На рис. 7.12 обозначена как новая кривая реакции (жирная линия), так и исходная (пунктирная линия). [c.123]
Поскольку изменилось положение только кривой реакции японской фирмы, нам предстоит определить изменения, произошедшие с состоянием равновесия. Их можно отследить на рис. 7.13, где объем производства японской фирмы измеряется на вертикальной оси, а объем производства американской — на горизонтальной. Как видим, точка N" нового равновесия располагается выше линии, проведенной под углом 45°, т.е. объем производства японской фирмы превышает объем производства американской. Ничего удивительного в этом нет, поскольку японская фирма снизила свои издержки (в долларах США), тогда как издержки американской фирмы остались неизменными. [c.123]
Рис. 7.14 дает представление о том, как этот динамический процесс может выглядеть. Мы начинаем с точки на горизонтальной оси (объем производства Фирмы 2 в нулевом периоде). В первом периоде мы смещаемся по вертикали в направлении кривой реакции Фирмы 1 (Фирма 1 приближается к оптимуму). Во втором периоде мы смещаемся по горизонтали в направлении кривой реакции Фирмы 2 (Фирма 2 приближается к оптимуму). В третьем периоде мы вновь смещаемся по вертикали в направлении кривой реакции Фирмы. 1. И так далее. Как видно из рисунка, в динамике ситуация стремится к равновесию Курно. По сути, вне зависимости от первоначальной ситуации мы постоянно стремимся к равновесию Нэша. [c.128]
Во-первых, вспомним, что прибыль Фирмы 1 составляет щ = P(Q)q - (q ), где Q — совокупный объем производства. С точки зрения Фирмы 1 это значит, что самое важное — это совокупный объем производства других фирм независимо от их общего количества и объема производства каждой. Другими словами, прибыль Фирмы 1 — это функция от Q, а не от и или каждого отдельного < , (/ 1). Это в свою очередь означает, что наш вывод кривой реакции справедлив для случая с и фирм при условии, что мы заменяем q2 на 0 = 2 =29/> т.е. на совокупный объем производства всех фирм за исключением Фирмы 1. (Обратите внимание, что в случае, когда и = 2, Q- = 2-) [c.155]
Поскольку мы по-прежнему имеем дело с симметричной олигополией, все фирмы в равновесных условиях производят один и тот же объем продукции, т.е. qtN= qN. Мы можем определить следующим образом. На рис. 9.1 чертим кривую реакции Фирмы 1 < i(Q-i)- Затем из точки начала координат проводим линию с наклоном 1/(и - 1), т.е. линию q = ( 1/(и - 1). Состояние равновесия образуется тогда, когда (1) Фирма 1 выбирает [c.155]
Если издержки входа очень высоки, зрелая фирма должна вести себя как монополист и игнорировать угрозу входа. Если издержки входа очень низки, то зрелая фирма должна принимать решения, учитывая кривую реакции потенциального новичка. Наконец, при промежуточных издержках входа зрелая фирма должна производить столько, чтобы побудить потенциального новичка воздержаться от входа. [c.265]
Решение зрелой фирмы относительно мощностей может повлиять на решение о входе на рынок фирм-новичков. Если издержки входа высоки, зрелая фирма должна вести себя как монополист и игнорировать угрозу входа. Если издержки входа очень низки, то зрелая фирма должна принимать решения, учитывая кривую реакции потенциального новичка. Наконец, при промежуточных издержках входа зрелая фирма должна производить столько, чтобы побудить потенциального новичка воздержаться от входа. [c.287]
Если кривые реакции изобразить графически (рис. 8.3. ), равновесие Курно достигается в точке их пересечения. Именно здесь ожидаемые объемы двух фирм совпадают с их реальными величинами. Механизм достижения равновесия можно показать следующим образом. Что произойдет, например, в точке А В этой точке фирма 1 произведет большее количество товара, чем от нее ожидает фирма 2. В результате фирма 2 будет вынуждена сократить свой объем выпуска в следующем периоде. В то же время фирма 1 в расчете на большое количество товара фирмы 2 тоже сократит свой выпуск. Когда и эти ожидания не оправдываются, фирмы будут корректировать объемы производства до тех пор, пока не будет достигнута точка равновесия, пока их ожидания не будут оправдываться. [c.151]
Уравнение предельной выручки и предельных затрат определяет, таким образом, объем производства первого дуополиста, если даны объем производства второго дуополиста и предположение первого об изменении этого объема. Таким образом, для любого отдельного типа предположений мы можем построить подобную используемой Курно кривую реакции и установить соответствие между объемом производства первого дуополиста и возможным производством второго. Аналогичная кривая реакции может быть построена для второго дуополиста, и пересечение обеих кривых даст точку равновесия. [c.345]
КРИВАЯ РЕАКЦИИ [rea tion urve] — кривая, отражающая функциональную зависимость между любыми двумя переменными, одна из которых принимается за аргумент, а другая — за его функцию. (К.р. может также описывать функцию многих переменных.) Напр., в модели Курно — кривая, характеризующая оптимальные объемы производства фирмы в зависимости от предполагаемых объемов производства [c.161]
Равновесие Курно [ ournot equilibrium] — некооперативное равновесие каждая фирма принимает решения, которые дают ей наибольшие прибыли при данных действиях своих конкурентов. График, отражающий объемы производства фирмы в зависимости от предполагаемых объемов производства ее конкурентов, называется кривой реакции. Равновесный уровень объема производства находится на пересечении кривых реакции обеих фирм. В теории игр такая ситуация называется равновесием Нэша (см. Нэшаравновесие). В конечном счете прибыли, получаемые каждой фирмой, выше, чем если бы они были при идеальной конкуренции, но они [c.165]
Равновесие Нэша представляет собой пару стратегий — в данном случае пару цен, при которых фирмы не могут увеличить прибыль путем одностороннего изменения цены. На рис. 7.2 оно дано точкой пересечения кривых реакции — точко й N. В сущности, в этой точке pl= p (pi) (поскольку точка находится на кривой реакции Фирмы 1) и р2 -= р (р ) (поскольку точка находится на кривой реакции Фирмы 2). Как можно видеть на рис. 7.2, точка N соответствует установлению обеими фирмами цены, равной предельным издержкам МС. [c.109]
Теперь рассмотрим альтернативную интерпретацию этой модели. Прежде чем Фирма 2 примет решение, входить или нет, Фирма 1 должна выбрать производственные мощности. Затраты на создание мощностей весьма высоки и эти инвестиции безвозвратны. Это значит, что даже если Фирма 1 позже решит снизить объем производства ниже достигнутого уровня производственных мощностей, ей не удастся вернуть затраты на расширение мощностей. Допустим также, что издержки производства, отличные от затрат на созданные мощности, равны нулю. При таких обстоятельствах у Фирмы 1 более сильная мотивация увеличить свой объем производства, чем прежде. Действительно, если все затраты на созданние мощностей оплачены, то, установив любой объем производства в рамках имеющихся производственных мощностей, Фирма 1 не понесет дополнительных издержек. Несмотря на то что нам по-прежнему необходимо более подробно разобраться с кривыми реакции Фирмы 1 и Фирмы 2, равновесное состояние, подобное представленному на рис. 15.1, теперь весьма возможно, более того, вероятно. Отметьте в дополнение к предпосылке, что издержки создания мощностей высоки, мы должны допустить, что эти издержки безвозвратны. Если бы затраты на создание мощностей не были безвозвратными, Фирма 2 могла все-таки войти на рынок и установить объем производства на уровне Курно. В этом случае для Фирмы 1 было бы лучше всего продать свои мощности, возместить издержки на инвестиции и также установить объем производства на уровне Курно. Таким образом, мы приходим к выводу [c.266]
Условие для отрицательного наклона таково, что выражение 1+ +hxi/x(l + 9a 2/9zi) должно быть положительным h — отрегулированная вогнутость рыночной кривой спроса. (Иными словами, h -= (zi + xt)f"(xi + z2)// (zi + z2). Ср. Robinson J. E onomi s... P. 40). Поскольку мы можем предположить, что во всех обычных случаях 1 + 3z2/9zi имеет положительное значение, отсюда следует — кривая реакции будет иметь отрицательный наклон всегда, когда h положительно (когда кривая спроса направлена выпуклостью кверху), а также в значительном числе случаев, когда h отрицательно. Позднее Аллен показал, что при отрицательном наклоне наклон кривой реакции будет также (из [c.345]
Если оба гипотетических изменения равны нулю, то мы имеем случай Курно. 2. Если одно из гипотетических изменений равно нулю, а другой дуополист принимает в качестве предположения действительный наклон кривой реакции своего конкурента, то мы имеем случай активной политики одного из дуо-полистов.30 В нормальных условиях это сделает отрицательным предположение активного дуополиста о реакции конкурента таким образом, по сравнению со случаем Курно это повысит его кривую предельной выручки, увеличит выпуск его продукции и (опять-таки в нормальных условиях) приведет к росту общего выпуска продукции, а также к снижению цены. 3. Если оба дуополиста действуют таким образом, исчисляя каждый предположительную реакцию конкурента по кривой реакции, то мы получим любопытный случай, исследованный д-ром фон Штакельбергом и Харродом.31 В нормальных условиях это еще раз приведет к дальнейшему увеличению общего выпуска и снижению цены. 4. Нет никакой причины, почему мы должны остановиться на этом. Один дуополист может стать вдвойне активным и подсчитать возможное изменение с помощью кривой реакции своего конкурента, исходя из предположения, что конкурент активен. В большинстве, хотя совсем не во всех нормальных случаях, это приведет к дальнейшему снижению цен. Похоже, что возникает процесс конкурентного снижения цен. [c.346]
