Это числитель коэффициента корреляции рангов. Подставив в (8.24) найденные выражения для числителя и для знаменателя, имеем [c.260]
Преимущество коэффициента корреляции рангов состоит в том, что ранжировать можно и по таким признакам, которые нельзя выразить численно можно проранжировать кандидатов на занятие определенной должности по профессиональному уровню, по умению руководить коллективом, по личному обаянию и т. п. При экспертных оценках можно ранжировать оценки разных экспертов и найти их корреляции друг с другом, чтобы затем исключить из рассмотрения оценки эксперта, слабо коррелированные с оценками других экспертов. Коэффициент корреляции рангов, как будет показано в гл. 9, применяется для оценки устойчивости тенденции динамики. [c.260]
В качестве примера рассчитаем коэффициент корреляции рангов по данным табл. 8.1 (табл. 8.4). [c.260]
| Таблица 8.4 Расчет коэффициента корреляции рангов по данным табл. 8.1 |  |
Вычислим коэффициент корреляции рангов Кендалла по данным табл. 8.4 [c.262]
При полном совпадении рангов уровней, начиная с наименьшего, и номеров периодов (моментов) времени по их хронологическому порядку коэффициент корреляции рангов равен +1. Это значение [c.345]
Если показатель факторного признака не может быть выражен в количественной форме, то вычисляют коэффициент корреляции рангов [c.74]
Как уже говорилось выше, коэффициент корреляции рангов рассчитывается в тех случаях, когда факторный признак не может быть выражен в количественной форме. Например, зависимость потребления обуви от места жительства потребителей характеризуется следующими данными. [c.76]
Коэффициенты корреляции рангов. [c.168]
Оба ранговых коэффициента корреляции применяются для решения одних и тех же задач. Преимуществом коэффициента Т является возможность его использования в многофакторном анализе. Например, при двухфакторном анализе (X,, Х2) частный коэффициент корреляции рангов У и X, равен [c.147]
Количественная степень рациональности структуры ассортимента может быть оценена коэффициентом корреляции рангов выпуска и ранга рентабельности. [c.34]
Из примера видно, что ранее рассчитанный коэффициент корреляции (0,4716) и коэффициент корреляции ранжирования (0,4643), исчисленный на основе тех же исходных данных, очень близки по своему значению. Однако возможны случаи, когда корреляция между рангами двух наборов данных не будет сопровождаться корреляцией между фактическими значениями этих наборов. В таком случае целесообразно увеличить выборку, получить дополнительную информацию и более убедительные результаты расчетов. [c.73]
В этой формуле п — количество значений и d — разница между парами рангов. Она дает такое же значение, что и коэффициент корреляции производного момента, рассчитанный на основе рангов. Как мы видим, эта формула гораздо проще и одновременно дает объективный показатель корреляции между двумя наборами данных. На последующих примерах мы рассмотрим вычисление коэффициента ранговой корреляции. [c.110]
Это значение г показывает, что между двумя наборами значений существует крайне незначительная корреляция. То есть кандидат с высоким местом по результатам одного из тестов может оказаться на любом месте по результатам другого. Следует отметить, что ранее рассчитанный коэффициент корреляции производного момента для данного набора значений составил 0.145. Таким образом, мы видим, что два коэффициента корреляции могут дать сходные результаты. Однако это происходит не всегда. Возможна ситуация, когда при наличии корреляции между рангами двух наборов данных между фактическими значениями корреляция окажется незначительной. В таком случае результаты трудно анализировать, и поэтому часто необходим сбор дополнительной информации, с тем чтобы получить более убедительные доказательства. [c.112]
Эта корреляция отражает корреляцию рангов, другими словами, показывает, соответствует ли ранг предприятия согласно одному коэффициенту рангу этого же предприятия по другому коэффициенту. [c.755]
Коэффициент корреляции между рядами рангов (фактическим и эталонным), рассчитанный по формуле, приведенной в разделе 2.8.1, равен 0,93. Такая величина коэффициента корреляции свидетельствует о том, что связь между изучаемыми рядами рангов весьма тесная Поэтому фактическую динамику показателей можно считать близкой к эталонной, s саму деятельность предприятия " льф" в 1999 г. можно признать в целом соответствующей плану. [c.415]
Часто необходимо исследовать связь качественных признаков социально-экономического явления, имеющих лишь неявную количественную меру. Эта мера может ощущаться интуитивно и проявляться в сравнительной интенсивности признака. Например, измерить способности людей мы не умеем, но часто с уверенностью утверждаем, что один человек способнее другого. То же относится и ко многим экономическим характеристикам — вредности производства, степени специализации, уровню прогрессивности технологии и т. п. В таких случаях множество анализируемых объектов исследователь может расположить в определенном порядке по интересующему его показателю, т. е. построить ранжированный ряд в соответствии с избранным критерием. При анализе связей таких признаков применить обычную корреляцию нельзя, поскольку она имеет дело лишь с количественными признаками. Различные коэффициенты связи, описанные выше, также вряд ли нас удовлетворят. Для этих целей математическая статистика располагает специальным аппаратом — корреляцией рангов. Мерой признака будем считать его относительную интенсивность у одного объекта наблюдения по сравнению с интенсивностью у другого объекта наблюдения. Тогда количественной характеристикой интенсивности может служить номер данного объекта наблюдения, который получил название ранга, а сам процесс расположения объектов наблюдения по относительной степени интенсивности — ранжирования. [c.91]
К мерам тесноты парной связи относится и предложенный английским психологом Ч. Спирменом (1863 - 1945) коэффициент корреляции рангов. Ранги - это порядковые номера единиц совокупности в ранжированном ряду. Если проранжировать совокупность по двум признакам, связь между которыми изучается, то полное совпадение рангов означает максимально тесную прямую связь, а полная противоположность рангов - максимально тесную обратную связь. Ранжировать оба признака необходимо в одном и том же порядке либо от меньших значений признака к большим, либо наоборот. Если ранги единиц совокупности по признакам х и у обозначить какр , р /( то коэффициент корреляции рангов согласно (8.11) имеет вид [c.259]
Недостатком коэффициента корреляции рангов является то, что одинаковым разностям рангов могут соответствовать совершенно отличные разности значений признаков (в случае количественных признаков). Поэтому для последних следует считать корреляцию рангов, как и коэффициент знаков Фехнера, приближенными мерами тесноты связи, обладающими меньшей информативностью, чем коэффициент корреляции числовых значений признаков. [c.260]
Коэффициент корреляции рангов по формуле Спирмена [c.260]
Рассмотрим пример расчета и анализа отклонений по ранее построенной модели уровня валового дохода в 16 хозяйствах. Знаки тех и других отклонений 8 раз совпадают и 8 раз не совпадают. Коэффициент корреляции рангов отклонений двух видов составил 0,156. Это означает, что связь вариации факторообеспеченности с вариацией фактороотдачи слабая, несущественная (табл. 8.13). [c.288]
Учеными разных стран за последние сто лет разработано несколько методов измерения связей таких признаков. Отметим прежде всего уже рассмотренный ранее коэффициент корреляции рангов Спирмена, применимый и к количественным, и неколичественным, но поддающимся ранжированию признакам. Так, например, можно при помощи одной группы экспертов проранжировать кандидатов на занятие какой-либо должности по степени профессиональной подготовленности, а другую группу экспертов просить проранжировать тех же кандидатов по личностным и этическим качествам, а затем измерить связь между рангами. [c.291]
Из определения понятия устойчивости тенденции вытекает и метод построения ее показателя. В качестве показателя устойчивости можно использовать коэффициент корреляции рангов Ч. Спирмэна (Spearman) - гх [c.345]
| Таблица 9.8 Расчет коэффициентов корреляции рангов Спирмена | 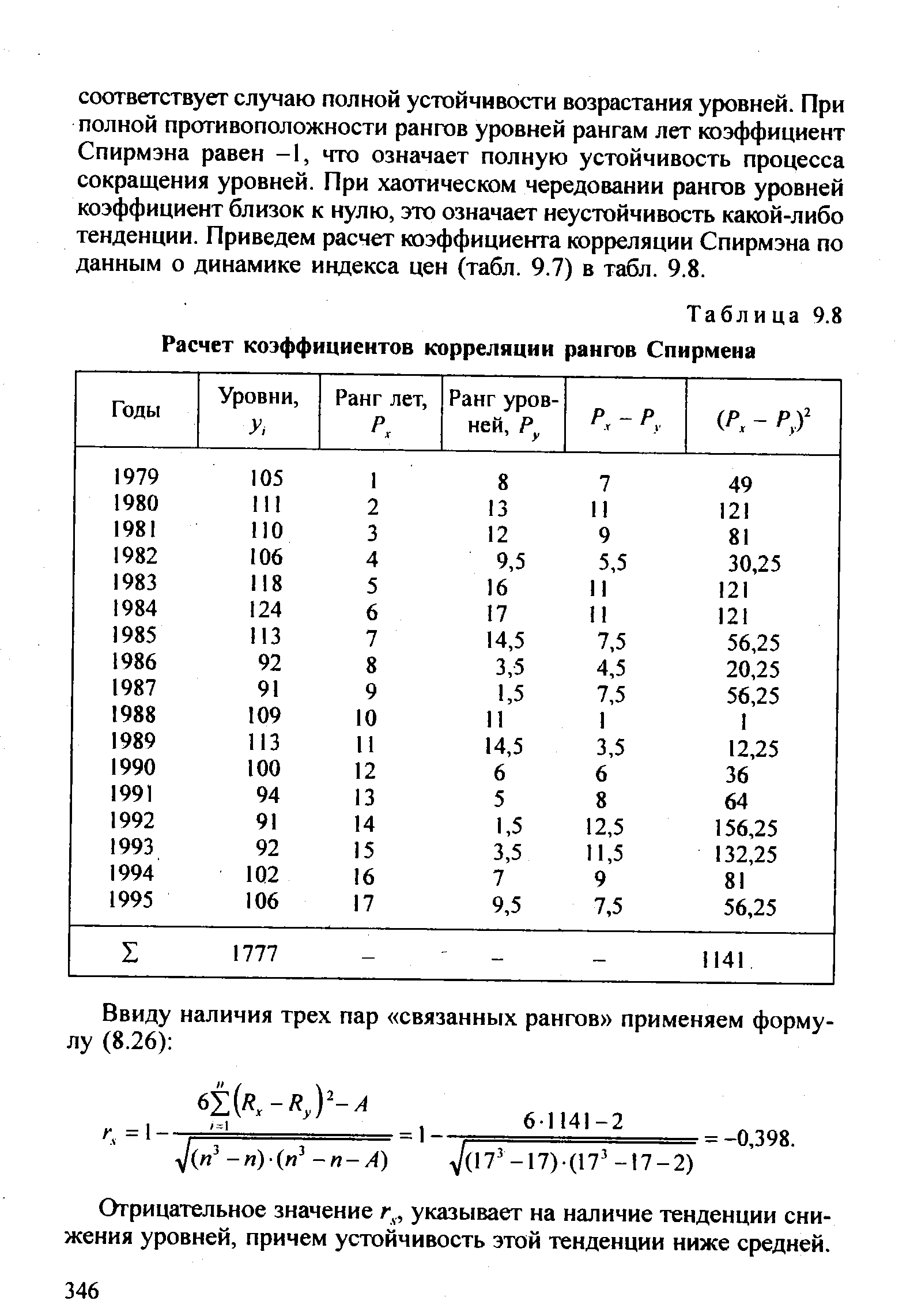 |
Коэффициент корреляции рангов (коэффициент Спирмена) рассчитывается по формуле (для случая, когда нет связных рангов) [c.127]
Для оценки связи между наиболее динамично растущими и наиболее емкими мировыми рынками лесных товаров используется коэффициент корреляции рангов Спирмена. Рассчитанное значение коэффициента незначительно (0,15). Таким образом, установлено, что связи между емкостью и темпом прироста данных рынков не существует. Затем проводится пространственный анализ показателей емкости рынка и темпа прироста рынка. В этом случае для оценки емкости рынка используется показатель средней за исследуемый период доли товара в обшей стоимости мирового экспорта (рис. II). В данном случае анализ осложняется сильной дифференциацией, например по средним темпам прироста, между целлюлозой (21%), необработанной древесиной (2%) и оставшимися 9 наименованиями лесных товаров (8—13%). Так что более естественным представляется выделение трех групп товаров и переход к матрице три на три , с включением дополнительно среднего уровня (рис. III). [c.201]
Таким образом, мы пришли к формуле коэффициента корреляции рангов Спирмена. Положив в формуле (14) Тх = Гу = 0, получим формулу (12). [c.94]
Существует способ исследования зависимости между признаками с помощью расчета так называемого коэффициента корреляции рангов Кендэла. Пусть заданы последовательности if и /, (/ = 1,п). Определим, что [c.94]
Тогда коэффициент корреляции рангов Кендэла равен [c.94]
Оценим те же связи с помощью коэффициентов корреляции рангов Кендэла. [c.99]
В табл. 29—31 приведены расчеты коэффициента корреляции рангов Кендэла. Эти коэффициенты также очень низки. Таким,образом, первоначальные выводы остаются в силе. [c.99]
Расчет коэффициента корреляции рангов Кендэла [c.100]
Расчет коэффициентов корреляции рангов,Кендэла [c.101]
В статистике известны коэффициенты корреляции, основанные на использовании рангов. Одним из таковых является коэффициент корреляции рангов Спирмена. Он основан на рассмотрении разности рангов значений факторного и результативного признаков и ее обозначают как dj. [c.27]
Тогда формула коэффициента корреляции рангов Спирмена (этот коэффициент именуют/)) имеет следующий вид [c.27]
Как и линейный коэффициент корреляции, коэффициент корреляции рангов может также меняться от -1 до +1. Используя шкалу Чеддока, по результатам расчетов коэффициента Спирмена можно предположить наличие заметной прямой зависимости между итогами работы студентов на данных фирмах. Однако следует учесть, что ранговый показатель был рассчитан по небольшому объему исходной информации (п = 12). Не является ли отличие [c.28]
Расчетная таблица для определения коэффициента корреляции рангов Спирмена [c.30]
Значения коэффициента корреляции рангов Спирмена для уровня значимости а и числа измерений п [c.97]
Сохранение и углубление межрегионального разрыва в уровне конкурентоспособности экономики регионов будет подтверждаться по -ложительным значением коэффициента корреляции рангов Спирмэна, а уменьшение этого снижения (или замедление его роста) — отрицатель - [c.27]
Для определения тесноты связи переменных, измеренных в шкале рангов используются коэффициенты корреляции рангов, в частности, коэффициент ранговой корреляции Кендала. [c.49]
Коэффициент ранговой корреляции Спирмена является непараметрическим аналогом коэффициента корреляции Пирсона и определяется не по величинам переменных признаков, а по рангам — номерам в порядке возрастания величин признаков. Он более детально оценивает связь по сравнения с коэффициентом Кендалла, но менее детально, чем коэффициент Пирсона. Коэффициент Кендалла определяется числом пар признаков, для которых характерны положительные и отрицательные связи. [c.87]
Ранговый коэффициент корреляции р может быть использован и для оценки тесноты связи между обычными количественными переменными. Достоинство р здесь заключается в том, что нахождение этого коэффициента не требует нормального распределения переменных, линейной связи между ними. Однако необходимо учитывать, что при переходе от первоначальных значений переменных к их рангам происходит определенная потеря информации. Чем теснее связь, чем меньше корреляционная зависимость между переменными отличается от линейной, тем ближе коэффициент корреляции Спирмена р к коэффициенту парной корреляции г. [c.80]
Для характеристики степени связи между элементами двух ранжировок нельзя использовать обычный коэффициент корреляции, поскольку ранги не являются непрерывными величинами (они дискретны). Вместо этого используют коэффициент ранговой корреляции Спирмена [c.147]
