| Рис. 8.2. Выбор оптимального портфеля | 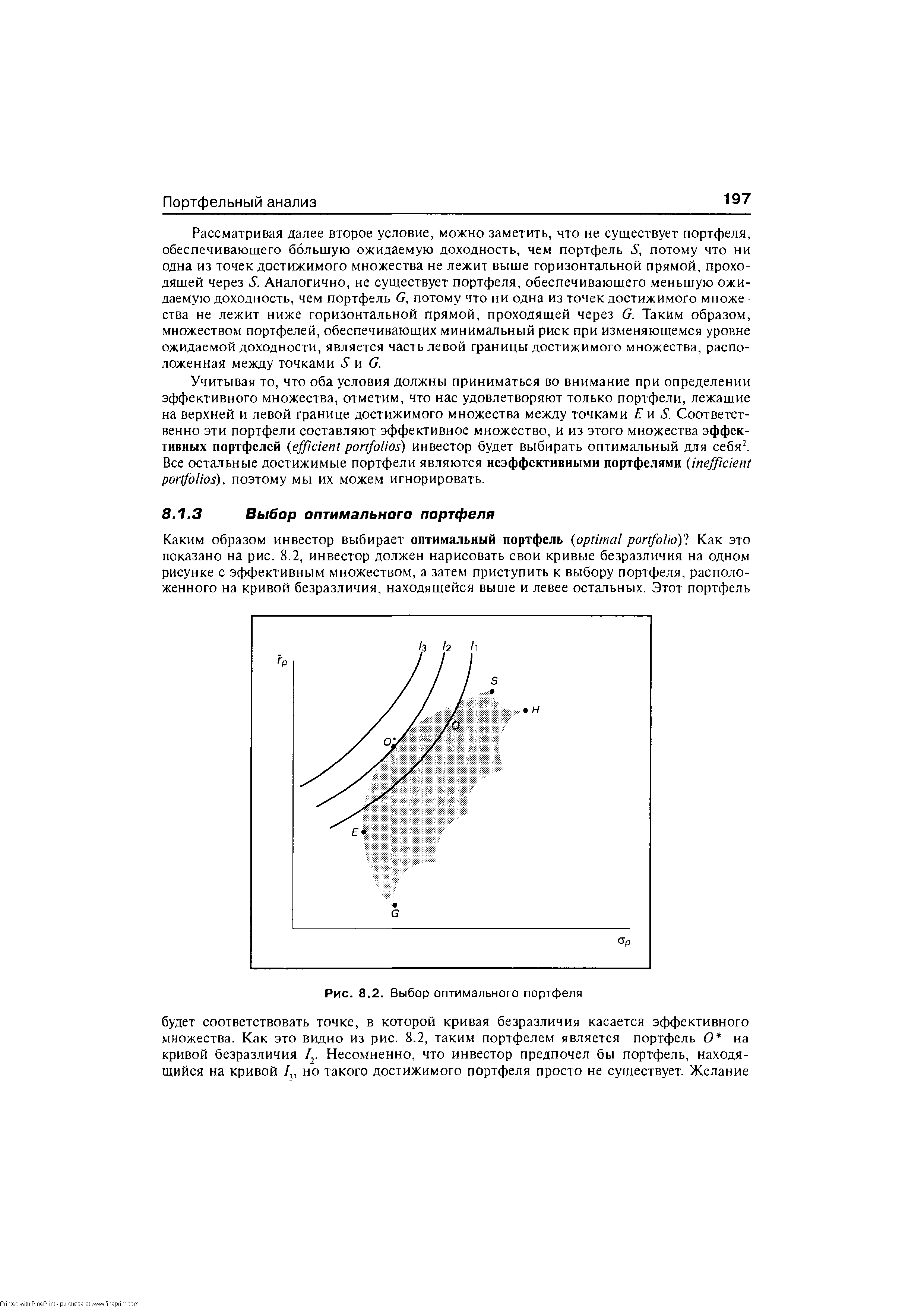 |
Оптимизация Выбор оптимального портфеля проектов [c.26]
Доходность ценных бумаг прямо связана с рискованностью вложений — это достаточно легко объяснить на основе концепции премии за риск. Для того, чтобы привлечь инвесторов, более рискованные ценные бумаги должны обеспечивать большую доходность по сравнению с надежными. Так как доходность есть отношение поступлений к цене данного актива, курсы рискованных ценных бумаг будут понижаться до тех пор, пока прибыльность вложений в них не окажется достаточной, чтобы компенсировать риск. Чем выше степень неприятия риска для данного экономического субъекта, тем больше доля надежных, но низко доходных ценных бумаг в его портфеле. Теория выбора оптимального портфеля в настоящее время широко используется в практике финансового планирования и прогнозирования колебаний биржевых курсов. [c.229]
ЭФФЕКТИВНЫЕ ПОРТФЕЛИ И ВЫБОР ОПТИМАЛЬНОГО ПОРТФЕЛЯ [c.66]
Оптимальный портфель — это единственный из эффективных портфелей, который является наилучшим для конкретного инвестора. При выборе оптимального портфеля решаются две независимые задачи [c.69]
Точка N на рис. 3.2, в которой кривая безразличия I, касается границы эффективного множества, отражает выбор оптимального портфеля рисковых активов, который обеспечивает инвестору самую высокую доходность при данной величине риска aN. Но инвестор может сделать лучший выбор он может достичь более высокой кривой безразличия, если в дополнение к возможному множеству рисковых портфелей воспользуется безрисковым активом, который обеспечивает гарантированную доходность aRF, — на оси доходности это точка, из которой исходит линия рынка капитала RMZ. Включение безрискового актива в портфель инвестора позволяет достичь комбинации риска и доходности на прямой линии рынка капитала инвестор перейдет из точки N в точку R, которая находится на более высокой кривой безразличия риск—доходность . [c.71]
Проблемы в выборе оптимального портфеля. [c.168]
Рис 2 10 Выбор оптимального портфеля на рис новых активов [c.63]
| Рис. 6.5. Выбор оптимального портфеля при других кривых безразличия | 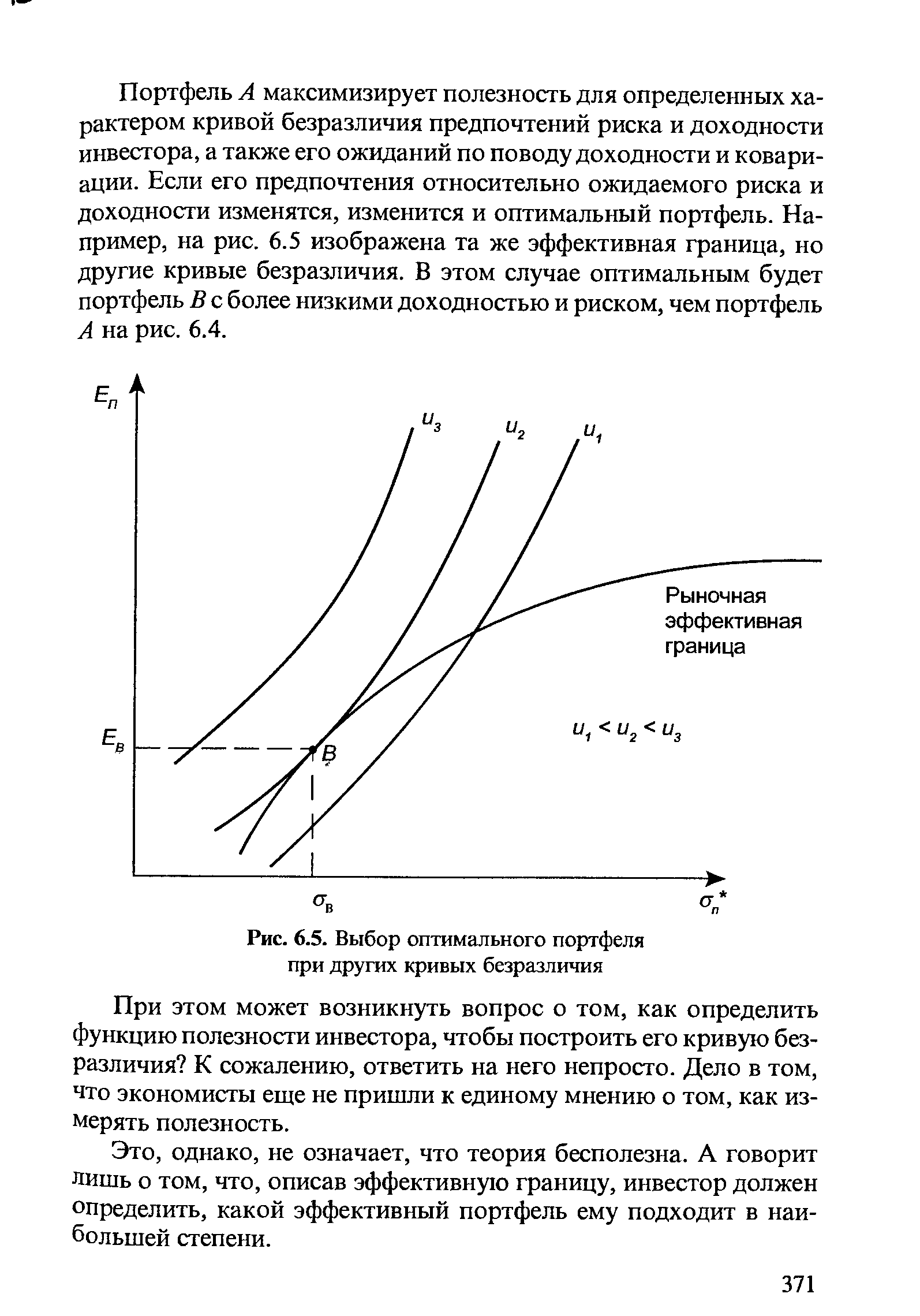 |
МОДЕЛИ ВЫБОРА ОПТИМАЛЬНОГО ПОРТФЕЛЯ ЦЕННЫХ БУМАГ [c.339]
Нынешнее состояние финансового рынка заставляет быстро и адекватно реагировать на его изменения, поэтому роль управления инвестиционным портфелем резко возрастает и заключается в нахождении той грани между ликвидностью, доходностью и рискованностью, которая позволила бы выбрать оптимальную структуру портфеля. Этой цели служат различные модели выбора оптимального портфеля. [c.340]
Рассмотрим некоторые из известных моделей выбора оптимального портфеля ценных бумаг. [c.340]
Выбор оптимального портфеля. Для выбора из множества альтернативных вариантов оптимального инвестиционного портфеля необходимо на одном графике совместить как само допустимое множество анализируемых портфелей, так и множество, или семейство, кривых безразличия, формализующих предпочтения инвестора. [c.206]
Рассмотрим простейшую модель выбора оптимального портфеля ценных бумаг. Условно разделим все финансовые активы на две группы. К первой группе отнесем безрисковые активы. Такие активы обладают очень низкой ожидаемой доходностью, и мы будем считать, что их ожидаемая доходность равна нулю. Эту группу активов мы и будем называть деньгами. Обозначив ожидаемую доходность через ге, а риск (который измеряется как корень из дисперсии, то есть, среднеквадратическое отклонение) через а мы можем дать характеристику первого актива (денег) г = 0, <зм = 0. Второй актив, который будем условно называть облигациями, характеризуется большей доходностью и большим риском г >0,<зв > 0. Обозначим через а (0<а<1) долю вложений в безрисковый актив (деньги), тогда доля вложений в рисковый актив (облигации) будет равна (1-а). Если W- богатство индивид, то вложения в безрисковый актив будут равны a W. [c.130]
Наложив на этот же график кривые безразличия, мы можем проиллюстрировать выбор оптимального портфеля (смотри рисунок 5). Итак, оптимум достигается в точке касания кривой безразличия с границей множества допустимых портфелей. Как мы видим, в оптимальной точке а строго больше нуля, но меньше единицы. Это означает, что потребитель выбирает стратегию диверсификации, то есть старается сократить риск путем вложений в разные активы, в том числе в безрисковый актив (то есть, деньги). [c.132]
Модель инвестора (выбор оптимального портфеля) [c.255]
Теория выбора оптимального портфеля в настоящее время начинает использоваться в практике полиграфических предприятий. Доходность ценных бумаг прямо связана с рискованностью вложений, [c.271]
Выбор оптимального портфели 255 [c.8]
В 1952 г. Гарри Марковиц опубликовал фундаментальную работу, которая является основой подхода к инвестициям с точки зрения современной теории формирования портфеля. Подход Марковица начинается с предположения, что инвестор в настоящий момент времени имеет конкретную сумму денег для инвестирования. Эти деньги будут инвестированы на определенный промежуток времени, который называется периодом владения (holdingperiod). В конце периода владения инвестор продает ценные бумаги, которые были куплены в начале периода, после чего либо использует полученный доход на потребление, либо реинвестирует доход в различные ценные бумаги (либо делает то и другое одновременно). Таким образом, подход Марковица может быть рассмотрен как дискретный подход, при котором начало периода обозначается / = 0, а конец периода обозначается / = 1. В момент = 0 инвестор должен принять решение о покупке конкретных ценных бумаг, которые будут находиться в его портфеле до момента / = 1. Поскольку портфель представляет собой набор различных ценных бумаг, это решение эквивалентно выбору оптимального портфеля из набора возможных портфелей. Поэтому подобную проблему часто называют проблемой выбора инвестиционного портфеля. [c.169]
На рис 2.10 изображена совокупность возможных портфелей в случае двух активов Он демонстрирует, как могут быть использованы кривые безразли чия для выбора оптимального портфеля из возможного множества. На рис 3 1 построен подобный график для случая большего числа активов, а кроме того, добавлен безрисковый актив с доходностью A.-RF Безрисковый актив, по опреде лению, имеет нулевой риск, и, следовательно, о — 0%, поэтому он может быть изображен точкой на вертикальной оси. [c.76]
Третий подход к анализу противоречий ЦМРК состоял в том, чтобы, сохраняя ее методологические основы, придать больший реализм предположениям, используемым в модели. Это означает сохранение базового предположения ЦМРК о том, что инвесторы (или их представители) следуют принципам выбора оптимального портфеля ценных бумаг. Однако в модель вводятся дополнительные факторы, которые усложняют ситуацию, делая ее реалистичнее. Одна из полученных таким образом моделей носит название межвременной ценовой модели рынка капитала. В этой динамической модели равновесные премии за риск, который несут инвесторы, приобретая ценные бумаги, формируются с учетом нескольких возможных вариантов измерения рискованности вложений. При этом на риске сказывается не только чувствительность к доходности рыночного портфеля или величина его коэффициента бета , но и чувствительность акций [c.408]
