Допустимое множество портфелей включает в себя все портфели, которые можно составить исходя из данного набора активов [c.64]
Набор всевозможных портфелей, которые можно сформировать сочетанием активов 1 и 2, имеет замысловатое название — допустимое множество портфелей. Оно объединяет все комбинации риска и доходности, которые могут быть получены выбором различных портфелей. Конечно, на практике инвесторы стремятся сосредоточить свое внимание на некотором важном подмножестве множества допустимых портфелей, а именно на множестве эффективных портфелей. В каждом из двух случаев, показанных на рис. 20-2, жирной линией выделена верхняя часть кривой портфеля. Она показывает допустимые портфели, являющиеся одновременно эффективными в том смысле, что они дают максимальную доходность при данном риске или минимальный риск при фиксированной доходности. Инвесторы всегда стремятся формировать эффективные портфели, с тем чтобы максимизировать ожидаемую доходность. Например, как следует из рис. 20-2в, инвестор никогда не остановит свой выбор на портфеле В (включающем 25% актива 1 и 75% актива 2), так как портфель С (включающий 75% актива 1 и 25% актива 2) также является доступным. Портфель С имеет тот же риск, но более высокую доходность по сравнению с портфелем В. В отличие от портфеля В портфель С является эффективным портфелем (так как нет способа получить более высокую доходность, не увеличивая при этом риск). На [c.695]
Предпочтения инвесторов показаны графически кривыми безразличия между ожидаемым доходом и стандартным отклонением. Их возможности представлены допустимым множеством портфелей из всех портфелей, которые могут быть подобраны путем различных комбинаций из имеющихся активов. Эффективным портфелем является та часть портфельного [c.710]
В данной статье предложена адекватная математическая модель распределения временно свободных денежных средств предприятия, найдена декомпозиция исходной задачи, сводящая ее решение к решению двух подзадач. Первую предложено решать на основе метода ветвей и границ (это позволит рассмотреть все допустимые множества исходов, удовлетворяющие ожиданиям инвестора), а вторую подзадачу (получение оптимального портфеля инвестиций в активы на заданном множестве исходов) - методом линейного программирования. [c.120]
Расположение эффективного множества на графике определяется требованиями, сформулированными в теореме о нем. Из приведенного графика видно, что портфель с минимальным уровнем риска расположен в точке Г (ни одна из точек допустимого множества не лежит вне точки Г) портфель с максимальным уровнем риска расположен в точке Б (ни одна из точек допустимого множества не лежит правее точки Б). Следовательно, множество портфелей, обеспечивающих максимальное значение уровня ожидаемой доходности в диапазон изменяющихся уровней их рисков, должно быть расположено на кривой между точками Г и Б (т.е. на верхней границе допустимого мно- [c.354]
В аА =20%, ав = 20%. Определить множество допустимых портфелей и выделить из допустимого множества эффективное подмножество при следующих значениях коэффициента корреляции гАВ = +1, гАВ = 0 и гАВ = — 1. Рассчитаем доходность и среднее квадратическое отклонение доходности портфеля при разных долях активов в его составе, используя формулы (3.7) и (3.12). Так, если доля актива А составляет 75% — хА = 0,75 и коэффициент корреляции гав = 1 То [c.66]
Добавим теперь портфель а с нулевым риском и гарантированной ожидаемой эффективностью а. Для нового множества допустимых Портфелей граница эффективности теперь изменится и будет описываться кривой ст—4. Для этого множества портфелей портфель 1 перестал б ыть эффективным, так как портфель а имеет меньший риск, чем портфель 1 при одинаковой норме доходности. [c.166]
Эффективный портфель по Марковицу — это допустимый портфель с наибольшей ожидаемой доходностью для заданного Уровня риска. Набор всех эффективных портфелей называется эффективным множеством портфелей, или эффективной границей. [c.373]
Плоскость (о2, ) называют критериальной. Меняя портфель, то есть меняя вектор х, получают различные оценки, а для них разные точки на критериальной плоскости. Множество всех оценок (то есть множество пар (а2, Е), а не множество портфелей) допустимых портфелей называют критериальным множеством. Если критериальное множество не сводится к одной точке, то возникает проблема выбора. Пусть По — некоторый портфель, а Со = (о2, ЕО) — оценка для П0. [c.468]
Выбор оптимального портфеля. Для выбора из множества альтернативных вариантов оптимального инвестиционного портфеля необходимо на одном графике совместить как само допустимое множество анализируемых портфелей, так и множество, или семейство, кривых безразличия, формализующих предпочтения инвестора. [c.206]
В общем случае коррелированное , графически различные комбинации доходности и риска достижимые комбинированием любых двух точек (активов) окажутся выпуклым множеством лежащим ниже- правее некоторой кривой соединяющей эти точки и выступающей, при не полной коррелированности, влево. Допустимое множество Р всех возможных комбинаций (портфелей), состоящих из рисковых активов для участника будет некоторой выпуклой фигурой. Комбинируя наилучшую по наклону 6 точку из Р с безрисковым активом как и ранее, получаем наилучший по соотношению риска и доходности (лучший для любого участника ) так называемый "рыночный" портфель. Этими рассуждениями доказывается следующее [c.63]
В общем случае допустимое множество 72.всех доступных инвестору портфелей, состоящих из рискованных активов, на диаграмме риск-доходность будет изображаться некоторой связной фигурой, граница которой оказывается кривой, выпуклой влево (см. напр. [c.279]
Утверждается, что САРМ практически невозможно проверить, так как а) единственно проверяемой гипотезой является та, что действительный рыночный портфель принадлежит эффективному множеству (в этом случае ожидаемые доходности ценных бумаг и их коэффициенты бета связаны положительной линейной зависимостью) б) действительный рыночный портфель не может быть измерен допустимым способом. См. [c.287]
Пусть инвестор осуществляет выбор из множества допустимых портфелей Р на основе [c.49]
Эффективная граница Г (Qn) совпадает с множеством точек вида (ffm[n (г), г) при г г т где г - ожидаемая доходность допустимого портфеля с наименьшим риском. [c.86]
Отметим, что, во-первых, множество эффективных портфелей составляет подмножество множества допустимых портфелей и, во-вторых, что на эффективной траектории допустимые портфели являются одновременно и эффективными в том смысле, что они дают минимальный риск при фиксированной ожидаемой доходности или максимальную ожидаемую доходность при данном риске. [c.369]
Для модели Блэка, когда допустимы любые значения xi и Х2 лишь бы xi + х2 = 1, имеем в двухмерном случае прямую на плоскости х, х2, которая составлена из множества допустимых пар. Удобно представить эту прямую в параметрическом виде xi = t, Х2 1 - t, тогда каждый портфель описывается так х = (t, 1 - /), t — принимает любые вещественные значения (в том числе и отрицательные). [c.467]
Выбор ценных бумаг может осуществляться несколькими способами. Перед активным менеджером стоит задача прогнозирования ожидаемой доходности, стандартного отклонения и ковариации всех доступных ценных бумаг. На основе этих прогнозов определяется эффективное множество, для которого будут построены кривые безразличия. Понятие эффективного множества связано со множеством всех оценок допустимых портфелей (речь идет о множестве оценок, а не портфелей), которое геометрически изображается множеством точек на критериальной плоскости. Поскольку инвестор при выборе ценных бумаг исходит лишь из оценок их доходности и риска, то множество показывает пределы эффективности его выбора. [c.358]
Далее из множества допустимых вариантов необходимо определить инвестиционный портфель, расположенный на кривой безразличия, проходящей выше и левее остальных (см. приведенный ниже рисунок). [c.206]
| Рис. 4. Множество допустимых портфелей, состоящих из комбинации безрискового актива с нулевой ожидаемой доходностью и рискового актива. | 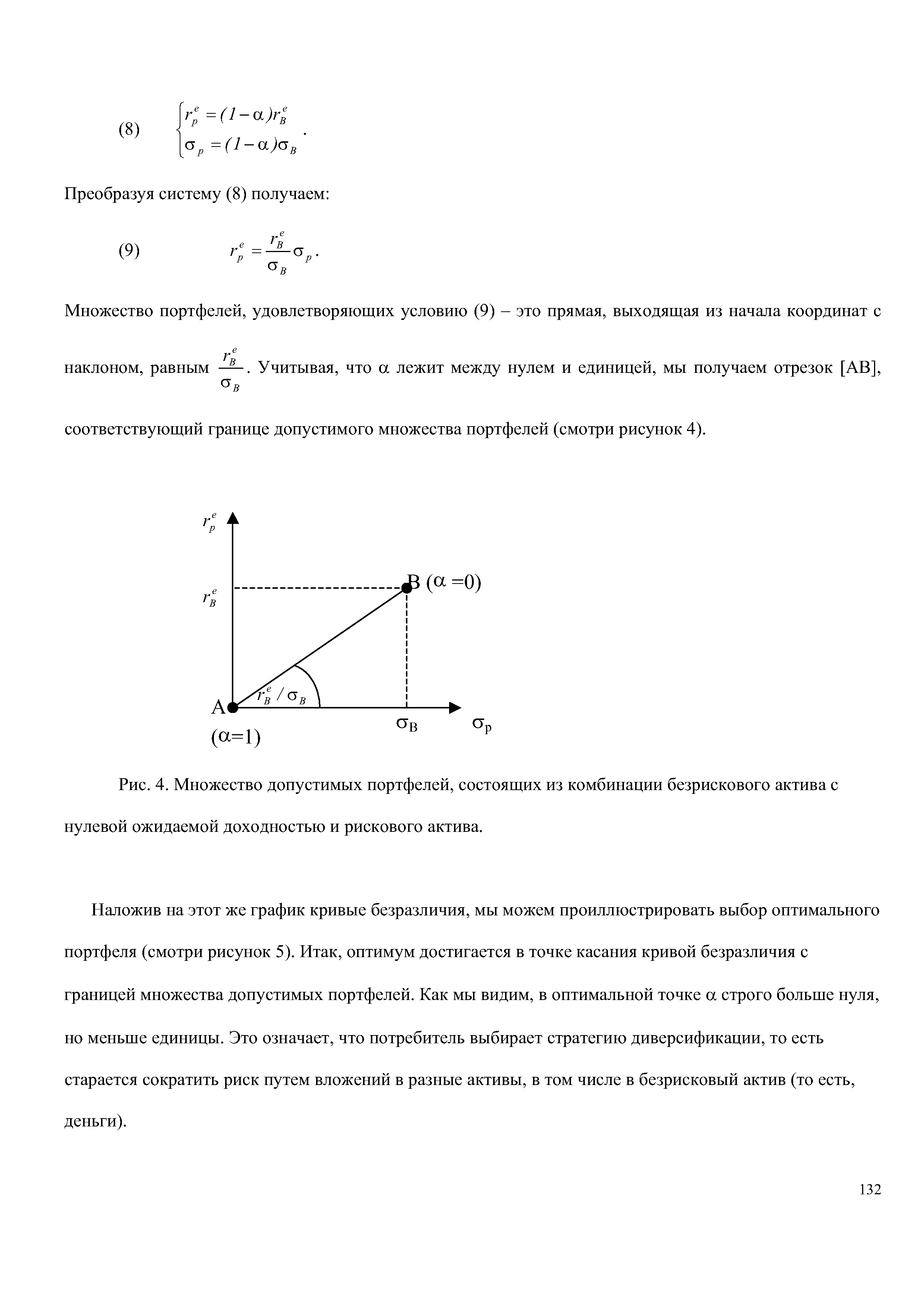 |
Какие же факторы влияют на наше решение об оптимальном распределении богатства между различными активами и, в частности, о вложениях в безрисковый актив, то есть, в деньги. Во-первых, это ожидаемая доходность и риск альтернативных активов (в нашем примере это облигации). Действительно, увеличение ожидаемой доходности и/или снижение риска по облигациям ведут к изменению наклона границы множества допустимых портфелей (наклон растет) и, соответственно, влияет на оптимальную долю безрискового актива. Считая активы валовыми заменителями, мы приходим к выводу, что спрос на деньги (то есть доля безрискового актива а) будет падать при повышении доходности и/или снижении риска по другим активам. [c.133]
Мы рассматривали ситуацию, когда безрисковый актив имеет нулевую доходность, однако это не обязательно так. Проведенный выше анализ несложно обобщить на случай, когда безрисковый актив имеет доходность, отличную от нуля. Тогда наклон границы множества допустимых портфелей зависит от ожидаемой доходности рискового актива относительно ожидаемой доходности безрискового актива. Таким образом, спрос на безрисковый актив будет тем больше, чем выше собственная ожидаемая доходность денег и чем ниже ожидаемая доходность альтернативного актива. [c.133]
Как показано на рис 2 6, в, допустимое множество портфелей, состоящих только из двух активов, представляет собой прямую или кривую. При увеличении числа активов линия трансформируется в некоторую область, например показанную на рис. 2.8. Точки А, Н, G и Е соответствуют отдельным цен ным бумагам (или портфелям, состоящим только из одной ценной бумаги). Все остальные точки заштрихованной области, включая ее границы, соответствуют портфелям, состоящим из двух или более акций Эта область называется допу стимым, или возможным, множеством Каждая точка области соответ [c.60]
Граница B DE на рис. 2 8 определяет эффективное множество портфелей и называется также границей эффективности (effi ient frontier) 13 Портфели, ле жащие слева от эффективного множества, использовать невозможно, поскольку они не принадлежат допустимому множеству Портфели, лежащие справа от границы (внутренние портфели), являются неэффективными, поскольку суще ствуют другие портфели, которые при данном уровне риска обеспечивают более высокую доходность либо более низкий риск для данного значения доходности Например, портфели С и D более предпочтительны, чем портфель X [c.61]
Постройте приемлемый гипотетический график доходности как функции риска, измеренного средним квадратическим отклонением портфеля Теперь постройте для ил люстрации допустимое множество портфелей и покажите, какая часть допустимого мно жества является эффективной. Что делает отдельный портфель эффективным Не за ботьтесь о конкретных величинах при построении графика, просто проиллюстрируйте идею эффективных портфелей. [c.69]
Рисунок 9.7 изображает, как изменяется допустимое множество, если введена возможность как предоставления, так и получения займа по одной и той же безрисковой процентной ставке. Рассматриваются не только акции РАС и Able, но и все остальные рискованные активы и портфели. Множество достижимости представлено областью, расположенной между двумя лучами, выходящими из точки, соответствующей безрисковой ставке, и проходящими через точки, соответствующие акциям Baker и портфелю, обозначенному через Т. Эти два луча уходят в бесконечность при условии, что нет ограничений на величину получаемого займа. [c.244]
Возможное множество портфелей. По результатам расчетов построим графики (рис. 3.1), характеризующие допустимое, или возможное, множество портфелей, имеющих разную структуру. Но не все портфели, принадлежащие допустимому множеству, являются эффективными. Нижняя ветвь кривой на графике б и нижняя часть ломаной линии на графике в соответствуют неэффективным портфелям, тогда как верхние ветви линий этих графиков соответствуют эффективным портфелям, т.е. портфелям с более высокой доходностью при одном и том же уровне риска по сравнению с другими. Только эти портфели, образующие эффективное множество, следует рассматривать при формировании оптимального портфеля, Наи олее типичная картина связи доходности и риска портфеля активов показана на рис. 3.16, так как активы, для которых коэффициент корреляции принимает значение 1,0, на практике не встречаются. [c.66]
Являются ли все портфели, принадлежащие допустимому множеству, в равной степени хорошими Ответ однозначен нет Только часть допустимого множества, лежащую в вариантах II и III между точками У и В, можно счи тать эффективной. Участок между точками Л и У не является эффективным, поскольку при любом уровне риска на отрезке AY можно получить более высо кую доходность, принадлежащую отрезку У В Таким образом, ни у одного рационального инвестора не будет портфеля, принадлежащего отрезку AY Однако в варианте I все допустимое множество является эффективным — ни одно из сочетаний ценных бумаг не может быть исключено из рассмотре ния [c.57]
ДОПУСТИМОЕ МНОЖЕСТВО [feasible set] — термин, используемый в современной портфельной теории для характеристики общего поля вариантов портфелей, из которого может быть выделено эффективное множество. [c.377]
Общее поле поиска вариантов портфелей, из которых может быть выделено эффективное множество, определяемое термином допустимое (или достижимое) множество" [feasible set]. Оно характеризует всю совокупность вариантов портфелей, которые могут быть сформированы из конкретного числа рассматриваемых финансовых инструментов инвестирования. [c.354]
Как уже обсуждалось в данной главе, концепции эффективного множества н оптимального портфеля инвестора являются основополагающими в современной инвестиционной теории. Но как инвестор может реально оценить эффективное множество и выбрать оптимальный портфель. 3 8 начале 50-х гадов Гарри Марковшд описал решение данных проблем. Используя математический метод, известный как квадратичное программирование, инвестор может обработать ожидаемые доходности, стандартные отклонения и ковариации для определения эффективного множества. (См. приложение А к данной главе.) Имея оценку своих кривых безразличия, отражающую их индивидуальный допустимый риск (см. гл. 24), он может затем выбрать портфель из эффективного множества. [c.199]
Optimal Portfolio — оптимальный портфель. Допустимый портфель, являющийся наиболее предпочтительным для инвестора. Этот портфель определяется точкой касания эффективного множества и кривой безразличия инвестора. [c.985]
