Точка N на рис. 3.2, в которой кривая безразличия I, касается границы эффективного множества, отражает выбор оптимального портфеля рисковых активов, который обеспечивает инвестору самую высокую доходность при данной величине риска aN. Но инвестор может сделать лучший выбор он может достичь более высокой кривой безразличия, если в дополнение к возможному множеству рисковых портфелей воспользуется безрисковым активом, который обеспечивает гарантированную доходность aRF, — на оси доходности это точка, из которой исходит линия рынка капитала RMZ. Включение безрискового актива в портфель инвестора позволяет достичь комбинации риска и доходности на прямой линии рынка капитала инвестор перейдет из точки N в точку R, которая находится на более высокой кривой безразличия риск—доходность . [c.71]
Доминирование линий рынка капитала [c.191]
Все участники рынка будут занимать позицию на новой прямой эффективности. Она называется линией рынка капитала. Рисковый портфель М держится всеми инвесторами и называется рыночным портфелем. [c.193]
В данном случае эталоном для сравнения является наклон апостериорной линии рынка капитала. Эта линия проходит через точки (О, D ) и ( m, D ), ее наклон может быть вычислен как следующее отношение (D —D, )/О, где О — [c.274]
Линия рынка капитала [c.76]
Линия рынка капитала ( ML) отражает зависимость риск—доходность для эффективных портфелей, т е для портфелей, сочетающих рисковые и безрисковые активы [c.97]
Сравнение линии рынка ценных бумаг с линией рынка капитала /3 коэффи циент какого-либо актива может быть выражен как функция коэффициента корреляции этого актива с рынком следующим образом [c.100]
Известны и другие способы применения линии рынка капитала. В частности, отбирая финансовые активы в портфель, инвестор может находить, какой должна быть доходность при заданном уровне риска. [c.255]
Инвестор, менее склонный к риску, мог бы предоставлять займы по нерискованной ставке, используя деньги, полученные с помощью бумаг его портфеля. Это сместило бы его в точку D. Отметим, что и в этом случае комбинация безрискового займа и портфеля дает более высокий доход при меньшем риске, чем сам по себе исходный портфель. Можно предположить, что каждый будет делать капиталовложения в точке М и затем перемещать их выше или ниже линии рынка капитала. Таким образом, точка М будет представлять собой суммарный рыночный портфель. [c.120]
Эта формула известна как рыночная модель, или характеристическое уравнение. Она соответствует линии рынка капитала, показанной на рис. 6.3. [c.121]
Понятно, что доля риска в доходности соответствует наклону линии рынка капитала на рис. 10.8. Кроме 100% холдинга в М, инвестор имеет возможность займов для финансирования дополнительного холдинга в неограниченном объеме. Предел в табл. 10.6 составляет 300% холдинга в М с ожидаемым значением доходности 24% и ожидаемым средним квадратическим отклонением 15%. [c.166]
ЕСЛИ бы инвестор мог оценивать средние значения доходности и формировать дисперсионно-ковариационную матрицу для этих доходов по всем видам ценных бумаг на рынке, он мог бы создавать эффективный набор из этих видов ценных бумаг. При допущении возможности свободного от риска получения кредитов или предоставления займов на рынке инвестор смог бы определять единственный портфель на кривой эффективного множества портфелей, который имеет такие же характеристики риска-доходности, как и линия рынка капитала (это портфель, находящийся в точке касания линии рынка капитала с кривой эффективного множества). [c.168]
Модель САРМ устанавливает зависимость между риском актива (портфеля) и его ожидаемой доходностью. Линия рынка капитала ( ML) показывает зависимость между риском широко диверсифицированного портфеля, измеряемым дисперсией, и его ожидаемой доходностью. Линия рынка актива (SML) говорит о зависимости между риском актива (портфеля), измеряемым величиной бета, и его ожидаемой доходностью. [c.299]
Уравнение линии рынка капитала с учетом принятых обозначений, получается путем преобразования формулы ( ) с использованием соотношений ( ) и ( ) [c.68]
Линия рынка капитала ( ML) [c.72]
Линия рынка капитала в модели оценки капитальных активов [c.103]
| Рис. 4.5. Линия рынка капитала и эффективное множество портфелей | 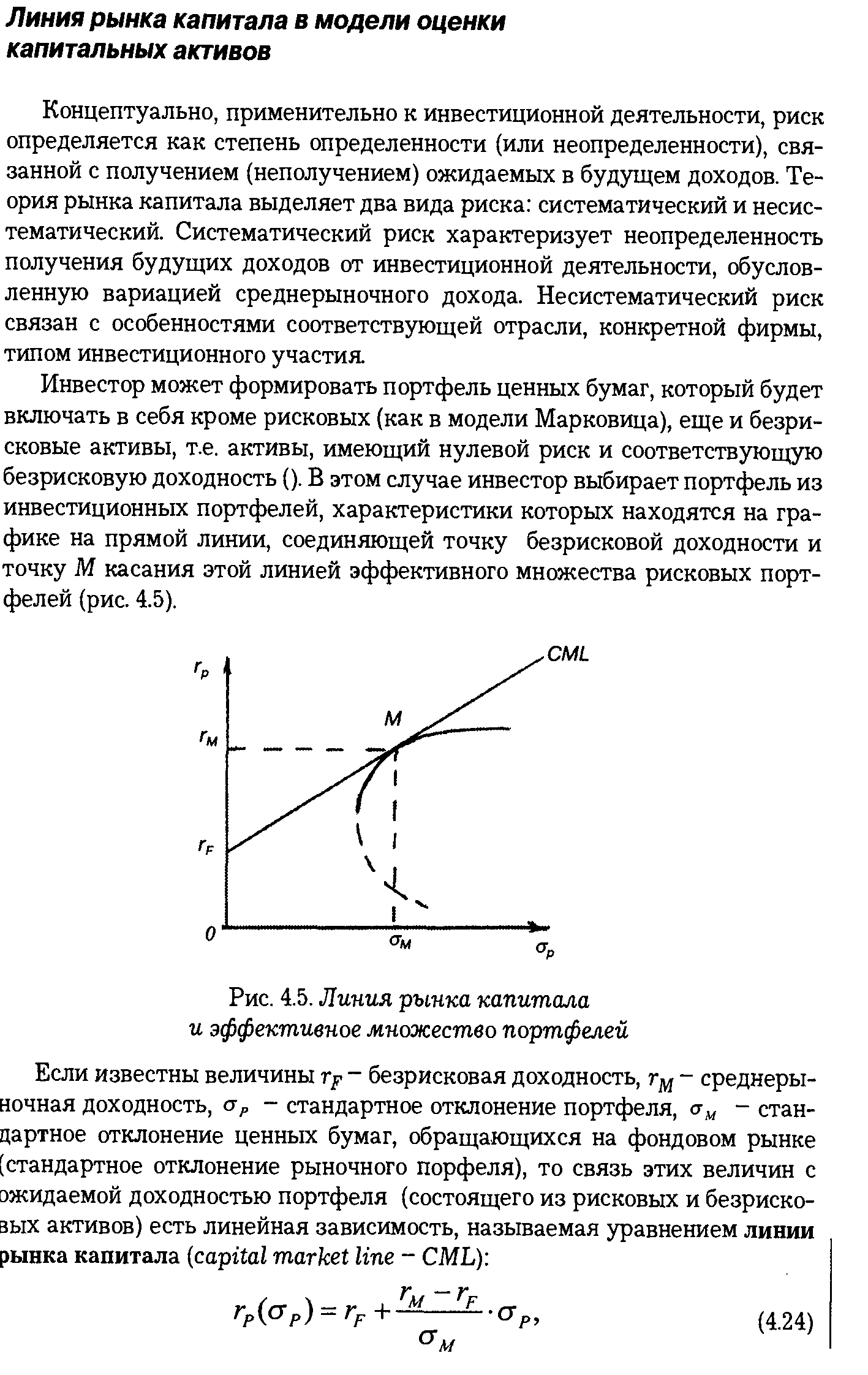 |
Рынок капитала представляет собой обыкновенный рынок, где люди заключают сделки с "сегодняшними" долларами и "будущими" долларами. Направленная вниз наклонная линия на рисунке 2-1 показывает существующий на рынке капиталов курс обмена между сегодняшними долларами и долларами следующего года ее наклон составляет 1 + г, где через г обозначена ставка процента первого года. Ссужая весь ваш сегодняшний приток денежных средств, вы можете увеличить ваше потребление в будущем на (1 + г )В, или на величину FH. Или же, беря заем под ваш будущий поток денежных средств, вы можете увеличить ваше потребление сегодня на F/(l +r), или BD. [c.16]
Сравнение метода затрат компании на капитал и метода требуемой доходности согласно модели оценки долгосрочных актинов. Для DE затраты на капитал составляют примерно 19%. Этот показатель можно использовать в качестве ставки дисконтирования только в том случае, если бета проекта равна 1,30. В целом правильная ставка дисконта растете ростом значения бета проекта. DE следует соглашаться на проекты со значениями нормы доходности, расположенными выше линии рынка ценных бумаг, которая связывает между собой требуемую доходность с величиной бета. [c.196]
Точка В соответствует касательному портфелю. Это единственный портфель, лежащий на эффективной границе, которого коснется линия, проведенная из точки с координатой безрисковая ставка прибыли на вертикальной оси и ноль на горизонтальной оси. Любая точка на отрезке АВ соответствует портфелю из точки В в комбинации с безрисковыми активами. В точке В все средства вложены только в портфель, а в точке А только в безрисковые активы. Любая точка между А и В соответствует определенной комбинации, когда часть активов находится в портфеле, а часть в безрисковых активах. Отметьте, что портфель на отрезке АВ более выгоден, чем любой портфель на эффективной границе при том же уровне риска, так как, находясь на отрезке АВ, он имеет более высокую прибыль при том же уровне риска. Таким образом, инвестору, который хочет получить менее рискованный портфель, чем портфель В, следует инвестировать средства в портфель В и в безрисковьте активы, а не смещаться по эффективной границе в точку с меньшим риском. Линия, выходящая из точки А безрискового уровня на вертикальной оси и нуля на горизонтальной оси и касающаяся в одной точке эффективной границы, называется линией рынка капитала ( ML). Справа от точки В линия ML представляет портфели, где инвестор занимает средства для инвестирования в портфель В. Отметьте, что инвестору, который хочет получить большую прибыль, чем дает портфель В, следует поступить именно таким образом, поскольку портфели на линии ML справа от точки В дают более высокую прибыль, чем портфели на эффективной границе при том же уровне риска. Как правило, В — очень хорошо диверсифицированный портфель. Большинство портфелей, расположенных справа сверху и слева снизу на эффективной границе, имеют очень мало компонентов, портфели в середине эффективной границы, где проходит касательная, достаточно хорошо диверсифицированы. Традиционно считается, что все разумные инвесторы хотят получить максимальную прибыль при данном риске и принять наименьший риск при заданной прибыли. Таким образом, все инвесторы хотят быть где-то на линии ML. Другими словами, все инвесторы хотят держать один и тот же портфель, но с различной долей заемных средств. Данное различие между инвестиционным решением и инвестированием с использованием заемных средств известно как теорема разделения. Мы будем исходить из того, что вертикальная шкала (Е в теории Е — V) выражает арифметическое среднее HPR (AHPR) для портфелей, а горизонтальная шкала (V) отражает стандартное отклонение HPR. Для заданной безрисковой ставки мы можем определить, где находится [c.202]
Линия рынка капитала ( apital Market Line — ML) — это линия RMZ на рис. 3.2, построенная в координатах риск—доходность . Она пересекается с вертикальной осью в точке, соответствующей доходности aRF. [c.71]
Эта линия называется линия рынка капитала ( ML apitel Market Line). Она включает в себя все возможные эффективные портфели, как безрисковые, так и рисковые активы. [c.247]
Основываясь на этих предположениях, САРМ продолжает делать заключения о поведении инвесторов. Во-первых, оптимальным портфелем для всех инвесторов должна быть некоторая комбинация рыночного портфеля (все рисковые активы калитализационно взвешены) и безрисковых активов. Этот тип портфеля показан на рис. 2.2. Линия рынка капитала касается эффективной границы рыночного портфеля (М), и точка ее пересечения с осью Y есть безрисковая ставка процента (г). Уровень риска можно менять путем добавления бе- [c.38]
Обобщением понятия линия рынка ценных бумаг является линия рынка капитала ( apital Market Line— M L), отражающая зависимость доходность/риск для эффективных портфелей, которые, как правило, сочетают безрисковые и рисковые активы. [c.255]
Линию рынка капитала можно использовать для сравнительного анализа портфельных инвестиций. Как следует из модели САРМ каждому портфелю соответствует точка в квадранте на рис. 5.12. Возможны три варианта расположения этой точки на линии рынка капитала, ниже или выше этой линии. В первом случае портфель называется эффективным, во втором — неэффективным, в третьем — сверхэффективным. [c.255]
Прямая, выходящая из точки rf на вертикальной оси, называется линией рынка капитала ( apital market line, ML). Эта линия прямая, потому что коэффициент корреляции доходности ценной бумаги, свободной от риска, и доходности любой рискованной бумаги всегда равен нулю. Выражение свободная от риска в данном случае подразумевает только отсутствие риска неуплаты, но не относится к другим типам риска. Точка М — это точка касания ML с границей эффективности, определенной без учета безопасных активов. Хотя существуют и другие портфели, состоящие из комбинации эффективных портфелей и безрисковых активов (другие точки на кривой АЕ), ни один из них не является столь же желательным, как портфели, расположенные на линии г,М. [c.229]
В САРМ зависимость между риском и ожидаемой доходностью графически можно описать с помощью линии ринка капитала ( apital Market Line — ML), которая представлена на рис. 55. М — это рыночный портфель, rf — актив без риска rf L — линия рынка капитала ат — риск рыночного портфеля Е(гт) — ожидаемая доходность рыночного портфеля. Все возможные оптимальные (эффективные) портфели, т. е. портфели, которые включают в себя рыночный портфель М, расположены на линии rfL. Она проходит через две точки — rf и М. Таким образом, линия рынка капитала является касательной к эффективной границе. Все другие портфели, в которые не входит рыночный портфель, располагаются ниже линии rf L. ML поднимается вверх слева направо и говорит о том, что если портфель имеет более высокий риск, то он должен предлагать инвестору и более высокую ожидаемую доходность, и если вкладчик желает получить более высокую ожидаемую доходность, он должен согласиться на более высокий риск. Наклон ML следует рассматривать [c.276]
Линия рынка капитала apital Market Line — это прямая на плоскости (а, //), связывающая уровень риска а с доходностью л для эффективных портфелей в смысле задачи Тобина. В нашем случае — это рыночный портфель и, как отмечалось выше, те портфели, у которых струк- [c.67]
В финансовом менеджменте нет и не может быть ничего застывшего, окончательного. Даже результаты, получившие в свое время нобелевскую премию в области экономики, попадают под удар сокрушительной критики. Так было, например, с портфельной теорией Марковица [134 - 135], с теорией линии рынка капитала Шарпа-Литнера [131, 144], с теорией справедливой оценки стоимости европейского опциона Блэка-Шоулза-Мертона [111]. Оказывалось, что предпосылки, положенные в основу этих теорий (нормальность законов распределения доходности активов, монотонность инвестиционных предпочтений, винеровский случайный процесс ценовых колебаний) существенно расходятся с реальностью фондового рынка [117, 118, 156]. Инвесторы, следовавшие классическим теориям фондового менеджмента, потерпели колоссальные убытки в 2001 - 2002 годах (только в США за эти годы инвесторы потеряли 7-10 трлн. долларов), когда изменившаяся картина рынка вступила в противоречие с научной его картиной, бытующей по сию пору. Основополагающее значение перечисленных нобелевских теорий для финансового менеджмента никем не оспаривается. Однако из этого не следует, что невозможно развитие и появление новых теорий финансового менеджемента, оппонирующих уже существующим теориям. Такая ломка научных стереотипов, кризис экономической парадигмы, о которой писал Т.Кун в [45], воспринимается сложившимися экспертами весьма болезненно, потому что вынуждает их обновлять свое научное мировоззрение, доучиваться. Новые теории обесценивают роль предшествующих теорий в научном процессе, равно как и вклад в науку целых поколений ученых, работавших в русле, очерченном их предшественниками. Все это рождает латентный протест, который может в конечном счете выразиться в ошибочном экспертном заключении. [c.15]
Линия доходности рынка ценных бумаг (se urity market line) — в ценовой модели рынка капитала это линейная зависимость, показывающая, что премия за риск для любой ценной бумаги равна произведению ее коэффициента "бета" на премию за риск всего рыночного портфеля. [c.326]
Смотреть страницы где упоминается термин Линия рынка капитала
: [c.201] [c.78] [c.98] [c.39] [c.120] [c.170] [c.103] [c.104] [c.238] [c.239] [c.324]Смотреть главы в:
Рынок ценных бумаг производных финансовых инструментов -> Линия рынка капитала
