Теоретическое обоснование того, что случайные переменные подчиняются закону нормального распределения, основывается на центральной предельной теореме. Теорема утверждает, что математическое ожидание большого числа независимых выборок [c.192]
ЭТИ ДВА РОССИЙСКИХ МАТЕМАТИКА ВНЕСЛИ БОЛЬШОЙ ВКЛАД В ТЕОРИЮ СТАТИСТИКИ, В ТОМ ЧИСЛЕ В ОБОСНОВАНИЕ ВЫБОРОЧНОГО МЕТОДА ЗАКОН БОЛЬШИХ ЧИСЕЛ (ЧЕБЫШЕВ) И ЦЕНТРАЛЬНАЯ ПРЕДЕЛЬНАЯ ТЕОРЕМА (ЛЯПУНОВ) [c.3]
Построение логнормального распределения исходит из того, что случайные величины подчиняются закону нормального распределения. Этот факт доказывается центральной предельной теоремой. Согласно этой теореме математическое ожидание большого числа независимых выборок будет нормально распределено вне зависимости от действительного распределения данных, при условии конечной дисперсии. Это утверждение имеет самое непосредственное отношение к финансовым рынкам. [c.195]
| Рис. 61. Равномерная плотность распределения вероятности результата измерения (7) и плотность распределения вероятности композиции двух (2) и трех (3) таких законов распределения вероятности (а - при Q = 0 б - при Q = 0,5) размахом является трапецеидальный закон. Это обстоятельство часто используется при учете дефицита информации. Рассматривая произведение большого числа характеристических функций, можно убедиться в том, что независимо от пида сомножителей оно стремится к характеристической функции, соответствующей нормальному закону распределения вероятности. Это фундаментальное положение носит название центральной предельной теоремы. На рис. 61 видно, как быстро нормализуется композиция одинаковых равномерных законов распределения вероятности. При числе слагаемых больше 4-х уже можно считать, что она практически подчиняется нормальному закону. | 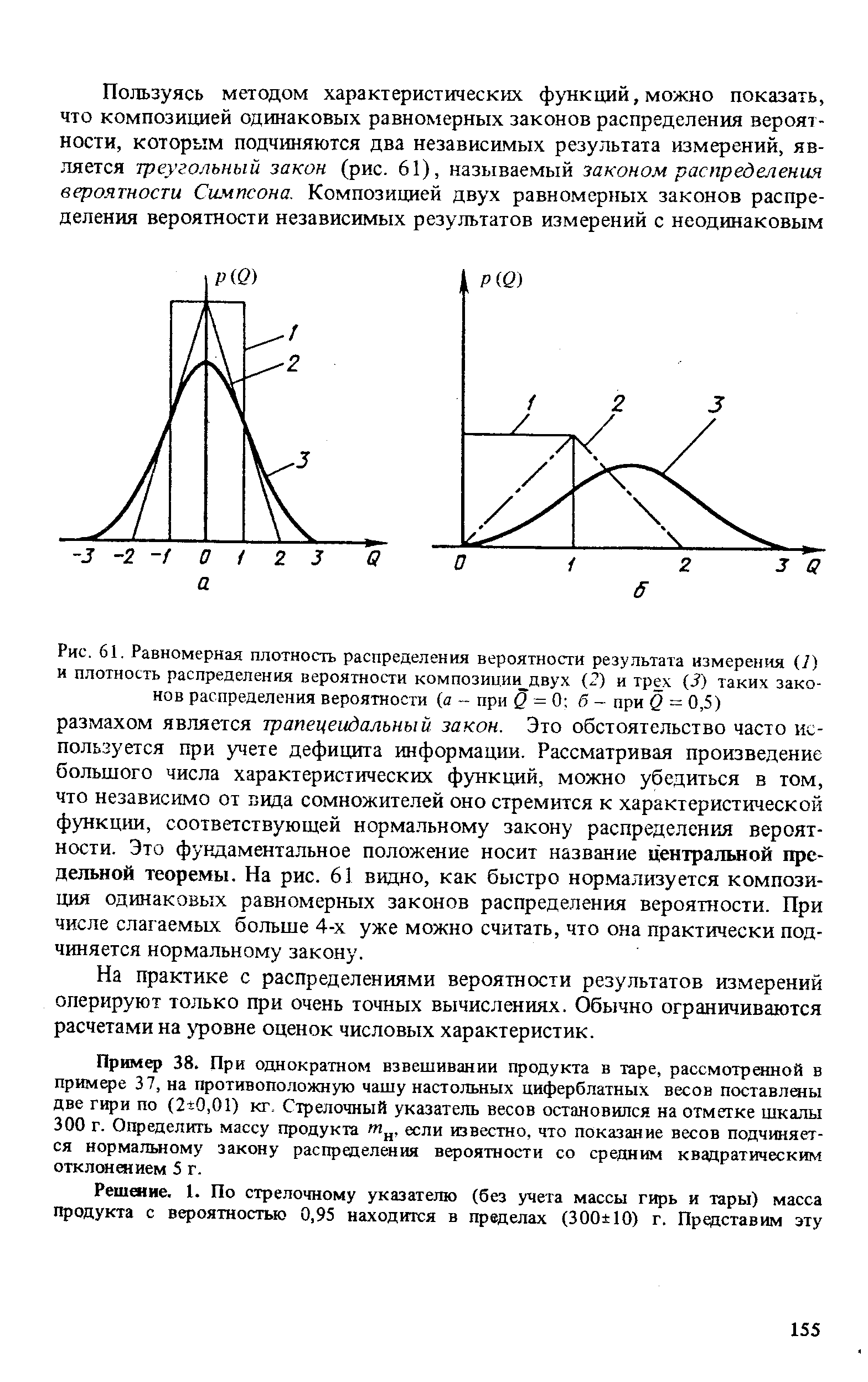 |
Смотреть страницы где упоминается термин Закон больших чисел. Центральная предельная теорема
: [c.429]Смотреть главы в:
Эконометрика начальный курс -> Закон больших чисел. Центральная предельная теорема
