В некоторых случаях нормальное распределение ошибок регрессии может следовать из некоторых теоретических соображений, — например, может использоваться центральная предельная теорема. Однако чаще всего нормальное распределение ошибок является модельным допущением, которое принимается в силу того лишь, что ему нет явных противоречий. В этом случае использование метода максимального правдоподобия требует определенной осторожности, и лучше использовать его в сочетании с другими методами. [c.205]
В табл. 3.2 приведены сводные результаты предварительной обработки статистической информации по группе технологических установок НПП. Распределения рассматриваемых случайных величин подчиняются нормальному закону (по отдельным продуктам это иллюстрируется данными, приведенными в приложении). Объективно это связано с тем, что рассматриваемые параметры отражают множество независимых случайных факторов — в этом случае в соответствии с центральной предельной теоремой закон распределения сколь угодно близок к нормальному. Необходимо отметить, что с учетом фактической точности исходной статистической информации, на основе которой определяются законы распределения в технико-экономических расчетах, и ограничений, налагаемых на условия функционирования производственно-экономических объектов, может осуществляться и приближенная замена одних законов распределения другими. [c.96]
Центральная предельная теорема (теорема Ляпунова) [c.29]
Это означает, что хотя существует только один главный фактор X, определяющий поведение отклика 7, но присутствует также большое количество малосущественных факторов, совокупное воздействие которых на отклик 7 согласно центральной предельной теореме имеет нормальное распределение. [c.106]
Если величины Ayk = ft(Pk I Pk ) независимы и имеют конечную дисперсию, то согласно центральной предельной теореме величина yt = n(Pt ) будет нормально распределена при любом [c.140]
Центральная предельная теорема [c.90]
Центральная предельная теорема, этот поразительно простой и красивый факт, подтверждает важность нормального распределения. [c.91]
Отсюда, согласно закону больших чисел в слабой форме или Центральной предельной теоремы теории вероятностей применительно к сумме независимых переменных (т. е. к числителю правой части выражения [1.15]), если максимизировать среднее геометрическое по всем периодам владения на достаточно большой выборке данных, то почти наверняка получим больший конечный капитал, чем с помощью любого другого решающего правила. [c.61]
Во многих проведенных нами имитационных тестах мы пользовались случайными выборками из нормального распределения. Такие выборки были получены на основе центральной предельной теоремы математической статистики. Эта теорема утверждает, что сумма независимых равномерно распределенных случайных величин является случайной величиной, распределенной нормально. Сгенерировав k равномерно распределенных случайных величин, мы получаем первую нормально распределенную величину из формулы , , , ,,,.,, > ) [c.95]
Идея контрольных карт базируется на центральной предельной теореме, из которой наиболее важны третьего аспекта [c.162]
Центральная предельная теорема 105 [c.495]
Из формулы (2.4) и центральной предельной теоремы теории вероятностей вытекает, что при увеличении объема выборки п распределение д сближается с нормальным распределением. Известно, что [c.344]
В теории вероятностей доказано функция распределения суммы большого числа независимых случайных величин близка к нормальному распределению при условии, что совокупность случайных величин обладает конечными моментами первого и второго порядков. Это утверждение носит название центральной предельной теоремы. Большинство рисков возникает именно как результат действия большого числа независимых случайных факторов и поэтому может быть описано нормальным распределением. Данному условию удовлетворяют отказы и аварии технических систем, потери на финансовом рынке, риски ущерба жизни и здоровью и др. [c.94]
Поскольку в алгоритмах используются только действия сложения и вычитания и применяются они к математическим ожиданиям длительности работ, то и результат любого расчета также будет представлять собой математическое ожидание случайной величины. Ее дисперсия будет равна сумме дисперсий работ, которые участвовали в расчете. Определенные таким образом параметры проекта в силу центральной предельной теоремы теории вероятности распределены по нормальному закону. Все сказанное справедливо лишь для достаточно больших проектов, где при расчетах параметров суммируются более десятка случайных величин — длительностей работ. Стохастическая постановка управления проектами позволяет решить две специфические задачи 1) определить, с какой вероятностью проект будет завершен к плановому сроку 2) рассчитать, к какому сроку проект может быть завершен с заданной вероятностью. Для решения обеих задач используется - нормированное отклонение случайной величины, распределенной нормально, или квантиль. Если задан плановый срок Тш, то выполняется расчет [c.131]
Таким образом, (Л, 6, с) может быть представлено в виде суммы большого числа случайных величин с малым рассеиванием. Согласно центральной предельной теореме имеются основания полагать, что L (A, b, с) — нормально распределенная случайная величина. Если случайные элементы набора (А, Ь, с) независимы, то дисперсия L (A, b, с) может быть вычислена по формуле [c.299]
В литературе по стохастической аппроксимации наметились два подхода к анализу скорости сходимости итеративных методов. Первый подход (см., например, [322]) основан на непосредственном изучении асимптотического поведения моментов т( . При втором подходе (см. [244]) асимптотические свойства оценок изучаются при помощи аппарата типа центральной предельной теоремы теории вероятностей. [c.362]
После того, как все влияющие факторы учтены и все поправки в показания внесены, рассеяние результата измерения одной и той же физической величины постоянного размера нередко бывает следствием множества причин, вклад каждой из которых незначителен по сравнению с суммарным действием всех остальных. Центральная предельная теорема теории вероятности утверждает, что результат измерения при этом подчиняется так называемому нормальному закону [c.75]
Стандартная гауссова статистика лучше всего работает на основе весьма ограничивающих предположений. Центральная предельная теорема (или Закон больших чисел) утверждает, что по мере проведения все большего числа испытаний, предельное распределение случайной системы будет нормальным распределением, или колоколообразной кривой. Измеряемые события должны быть "независимы и идентично распределены" (IID). То есть события не должны влиять друг на друга, и они все должны иметь одинаковую вероятность наступления. Долгое время предполагалось, что большинство крупных, комплексных систем должны моделироваться таким образом. Предположение о нормальности, или почти нормальности, обычно делалось при исследовании крупной, комплексной системы, так чтобы мог быть применен стандартный статистический анализ. [c.61]
В таблице 15.1 и на рисунке 15.1 показан эффект диверсификации для различных а и N с использованием уравнения (15.6). Читатель также может получить эти числа просто в электронной таблице. Как и предсказывалось, для a < 1,0 диверсификация действительно уменьшает нерыночный риск портфеля. Степень диверсификации уменьшается по мере уменьшения а до тех пор, пока, при a = 1,0, диверсификация ничего не делает для портфеля. Центральная предельная теорема не выполняется, когда a = 1, и работает в обратном направлении для a > 1. [c.212]
Нормальное распределение. Хорошо известная кривая имеющая форму колокола. В соответствии с центральной предельной теоремой функция плотности вероятности большого количества независимых, идентично распределенных чисел будет приближаться к нормальному распределению. В семействе фрактальных распределений нормальное распределение существует только тогда, когда альфа равна 2, или показатель Херста равен 0,50. Таким образом, нормальное распределение является частным случаем и, к тому же, в анализе временных рядов весьма редким. См. альфа , центральная предельная теорема , фрактальное распределение . [c.288]
Центральная предельная теорема. Закон больших чисел утверждает, что если объем выборки независимых, одинаково распределенных случайных чисел стремится к бесконечности, ее функция плотности вероятности приближается к нормальному распределению. См. нормальное распределение . [c.291]
В главе 2 мы обсудили гипотезу эффективного рынка (ЕМН), которая в своей основе утверждает, что поскольку текущие цены отражают всю имеющуюся в распоряжении или открытую информацию, будущие ценовые изменения могут определяться только новой информацией. Поскольку вся предшествующая информация уже нашла отражение в ценах, рынки следуют случайному блужданию. Каждодневное движение цены не имеет отношения к событиям предыдущих дней. Гипотеза эффективного рынка косвенным образом предполагает, что инвесторы немедленно реагируют на новую информацию, и, таким образом, будущее не связано с прошлым или настоящим. Это предположение было введено для того, чтобы применить к анализу рынка капитала центральную предельную теорему. Последняя была необходима для оправдания правомерности использования вероятностного исчисления и линейных моделей. [c.85]
Теоретическое обоснование того, что случайные переменные подчиняются закону нормального распределения, основывается на центральной предельной теореме. Теорема утверждает, что математическое ожидание большого числа независимых выборок [c.192]
Заметьте, что приведенный выше пример всего лишь описывает тенденцию собранных данных. Центральный предельный процесс описывает поведение средних собранных данных. [c.193]
Как мы уже отметили выше, в соответствии с центральной предельной теоремой процесс сложения изменений приводит к нормальному распределению. Что же произойдет в результате процесса умножения [c.197]
Предположим, что In(A i), ln(A"2) и т.д. являются IID, тогда мы сможем применить центральную предельную теорему для того, чтобы предположить, что n(S t)/ (t-i)) приблизительно нормально распределен. Центральная предельная теорема гласит, что если мы рассматриваем большую случайную выборку, то средняя величина ее будет нормально распределена. Таким образом, когда мы разделяем период времени на большое число промежутков (больше 30), с чем мы имеем дело, когда рассматриваем время как непрерывное, то сумма натуральных логарифмов в [c.198]
В гл. 4 мы узнали, что согласно центральной предельной теореме средние аддитивных процессов (арифметические средние) будут нормально распределены независимо от распределения исходных величин при условии, что выборки достаточно велики (объем выборки больше 30). Если первоначальная совокупность нормально распределена, а объем выборки меньше 30, распределение выборочных средних будет следовать -распределению Стьюдента. [c.225]
Таким образом, исходя из центральной предельной "теоремы мы можем сказать, что средняя достаточно большой выборки приближенно нормально распределена со средним значением, равным генеральной средней, и средним квадратическим отклонением, равным стандартной ошибке средней, т.е. [c.226]
Напомним, что проблема состоит в том, что мы не знаем среднюю генеральной совокупности, и нам известна только выборочная средняя. Тем не менее, согласно центральной предельной теореме мы знаем, что выборочное распределение средних имеет среднее значение, которое в свою очередь равно генеральной средней, а среднее квадратическое отклонение (стандартная ошибка) равно сг/>/л, где
Центральная предельная теорема может быть использована для доказательства утверждения о том, что выборочная средняя нормально распределена при условии, что объем выборки больше 30. В случае с малыми выборками необходимо допустить, что мы производим выборку из нормально распределенной совокупности для того, чтобы выборочная средняя была нормально распределена. Кроме того, только при выборках малого объема наша оценка генеральной дисперсии не будет надежной. В этом случае /-распределение позволит сделать поправку на эту дополнительную степень изменчивости. [c.232]
Общее впечатление заключается в том, что необходимо сделать гораздо более приемлемым второе из рассмотренных только что условий. В частности, если (хотя бы на границе эффективности) все портфели состоят из сравнительно большого количества ценных бумаг, центрально-предельная теорема означает, что вероятностные распределения доходов X для любого подобного хорошо диверсифицированного портфеля будут приближаться к нормальному распределению конечно, такое нормальное распределение будет касаться лишь двух параметров. Однако все это в действительности мало поможет нам чтобы объяснить данный вывод, приведем пример, предвосхищающий главные идеи следующего раздела. Предположим, что инвестор рассматривает неопределенное будущее как набор, вмещающий в себя три равно вероятных состояния мира — А, В и С, причем в действительности может иметь место только одно из этих состояний. Здесь состояние — это определенные характеристики окружающей среды, в рамках которой действует индивид. Для двух различных портфелей распределение будущих значений для состояний (ХА, ХВ, Хс) может быть равным соответственно (3, 2, 1) и (1, 2, 3). По- [c.241]
Нормальное распределение. Нормальное, или гауссово распределение, - это, несомненно, одно из наиболее важных и часто используемых видов непрерывных распределений. Оно симметрично относительно математического ожидания. Сначала остановимся на практическом смысле этого распределения применительно к экономическим задачам и сформулируем центральную предельную теорему теории вероятностей в следующей практической интерпретации. [c.28]
В различных математических постановках центральная предельная теорема рассматривается в научной литературе по теории вероятностей и математической статистике. [c.29]
Работа функции основана на применении центральной предельной теоремы. При получении одного числа используются 12 равномерно распределенных на отрезке (О, 1) величин, которые суммируются. Последовательность чисел, распределенных равномерно на отрезке (0,1), имеет математическое ожидание 1/2 и дисперсию 1/12. С учетом центральной предельной теоремы сумма таких 12 чисел имеет математическое ожидание б и дисперсию 1. После суммирования выполняются необходимые действия для обеспечения параметров нормального распределения математического ожидания т и дисперсии о2. [c.30]
Все вышесказанное верно независимо от того, как распределена совокупность данных Центральная предельная теорема позволяет нам обращаться с распределением средних значений выборок, как с нормальным, без необходимости знать распределение совокупности. Это чрезвычайно удобный факт для многих областей исследований. Если совокупность нормально распределена, то распределение средних значений выборок будет точно (а не приблизительно) нормальным. Кроме того, скорость, с которой распределение средних значений выборок приближается к нормальному при повышении N, зависит от того, насколько близко совокупность находится к нормальному распределению. Общее практическое правило следующее если совокупность имеет унимодальное (одновершинное) распределение (любой тип распределения, где есть концентрация частоты вокруг одной моды и уменьшение частот с любой стороны моды, например, выпуклость) или равномерно распределяется, то можно использовать N = 20 (это считается достаточным) и N = 10 (это считается достаточным с большой вероятностью). Однако если совокупность распределена экспоненциально (рисунок 3-6), тогда может потребоваться и N = 100. [c.91]
Ляпунова (иначе — центральная предельная теорема), которая утверждает, что распределение суммы п произвольно распределенных и взаимно независимых случайных величин при я—> <х> стремится к нормальному распределению, если вклад отдельных слагаемых в сумму равномерно мал а также теорема Че-бышева, позволяющая при большом количестве случайных величин использовать среднее арифметическое выборки в качестве оценки математического ожидания всей генеральной совокупности рассматриваемых величин. [c.105]
При использовании вероятностных моделей риска распространены два характерных заблуждения. Во-первых, если величина ущерба зависит от множества причин, то она должна иметь нормальное распределение. Это ошибочное мнение, так как все зависит от способа их взаимодействия. Если причины действуют аддитивно (суммарно), то согласно Центральной предельной теореме теории вероятностей величина ущерба действительно имеет приблизительно нормальное (гауссово) распределение. Если же причины действуют мультипликативно, то в силу той же теоремы следует приближать распределение величины ущерба X с помощью логарифмически нормального распределения. Если же основное влияние оказывает слабое звено , то согласно теоремам, доказанным академиком Б. В. Гнеденко, величину ущерба Xследует описывать с помощью распределения из семейства Вейбулла—Гнеденко. [c.276]
Если условия центральной предельной теоремы выполняются, то весь массив экспериментальных данных при многократном измерении одной и той же величины постоянного размера должен группироваться около некоторого среднего значения, и выпадение какого-нибудь отдельного значения результата из этого массива позволяет предположить, что он ошибочный. Найдем вероятность, с которой любое значение резулыата измерения, подчиняющегося нормальному закону распределения вероятности, должно находиться в пределах от Ql до Qi [c.75]
| Рис. 61. Равномерная плотность распределения вероятности результата измерения (7) и плотность распределения вероятности композиции двух (2) и трех (3) таких законов распределения вероятности (а - при Q = 0 б - при Q = 0,5) размахом является трапецеидальный закон. Это обстоятельство часто используется при учете дефицита информации. Рассматривая произведение большого числа характеристических функций, можно убедиться в том, что независимо от пида сомножителей оно стремится к характеристической функции, соответствующей нормальному закону распределения вероятности. Это фундаментальное положение носит название центральной предельной теоремы. На рис. 61 видно, как быстро нормализуется композиция одинаковых равномерных законов распределения вероятности. При числе слагаемых больше 4-х уже можно считать, что она практически подчиняется нормальному закону. | 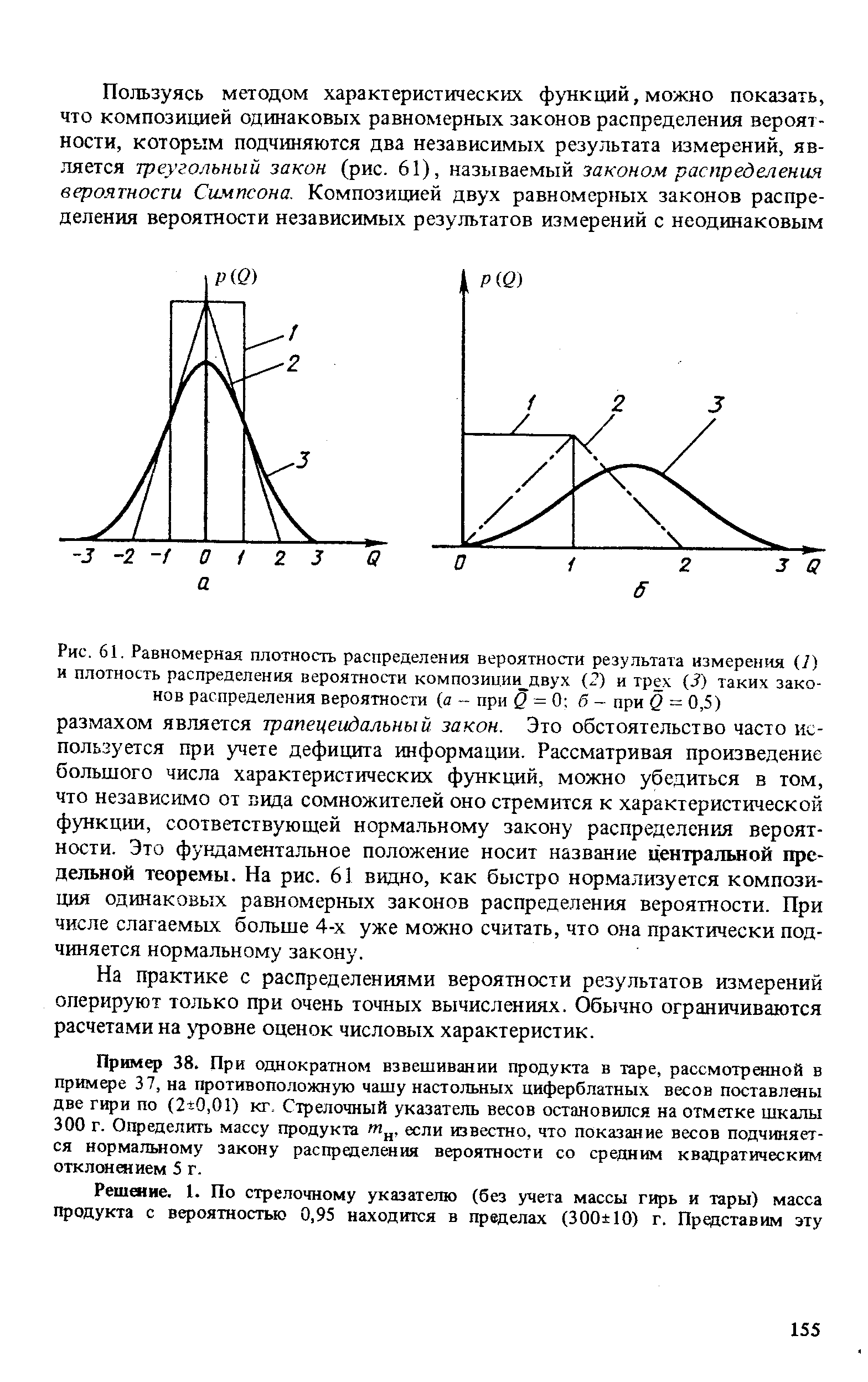 |
Предположение 7 Осборна является кульминацией предположений 3-6. В действительности оно является заключением и утверждает, что так как ценовые изменения независимы (т. е. они представляют собой случайные блуждания), следует ожидать нормального распределения этих изменений с устойчивым средним значением и конечной дисперсией. Это не что иное как следствие центральной предельной теоремы теории вероятностей, или закона больших чисел. Эта теорема гласит, что выборка независимых идентично распределенных случайных переменных (IID) будет нормально распределенной, если эта выборка достаточно велика. [c.33]
Для демонстрации центральной предельной теоремы рассмотрим ежеминутные изменения индекса FTSE 100. Допустим, что в течение следующей минуты индекс либо возрастет, либо упадет на один пункт с одинаковой вероятностью. Эта вероятность описывается следующим образом [c.193]
