Другое направление решения задачи линейного программирования с переменными векторами условий, заданными на сепарабельных выпуклых множествах, связано с предварительным определением всех вершин" допустимых значений технологических коэффициентов и последующим формированием и решением задачи линейного программирования, в которой для процессов с переменными технологическими коэффициентами рассматривается несколько вариантов, полученных в результате определения вершин" [17-20]. Одна из первых задач подобного типа [17] включала элементарный случай варьирования технологических коэффициентов, когда область их допустимых значений представляла собой многогранник, образованный пересечением и-мерного параллелепипеда одной гиперплоскостью. [c.15]
Производственно-экономические возможности объектов управления (установка, производство, предприятие, комплекс предприятий или отрасль) при использовании этого подхода могут быть аппроксимированы с помощью одного ограничения — гиперплоскости или многогранника. [c.18]
Выпуклые области, задаваемые условиями типа (2.1), (2.3), могут быть аппроксимированы в соответствии с основными положениями формализации, рассмотренной в [1, 33], с помощью одной гиперплоскости или выпуклого многогранника. [c.18]
Аппроксимирующая гиперплоскость, построенная с учетом производственной взаимозаменяемости ресурсов, способов производства и продукции и описывающая k-e предприятие на единичном отрезке времени, имеет вид т [c.19]
Преимущество аппроксимации производственных возможностей с помощью одной гиперплоскости заключается в наглядности и простоте недостатки связаны с увеличением погрешности аппроксимации по мере отклонения плана от опорного его значения. [c.19]
При отличных от нуля значениях Д гиперплоскость hx < 1 является секущей k области/ ( ). [c.19]
Во всех случаях построения аппроксимирующей гиперплоскости возникает необходимость исследования окрестности оптимального (в некотором смысле) исходного плана. [c.20]
Коэффициенты аппроксимирующей гиперплоскости й в простейшем случае могут быть вычислены как величины, обратные максимальному выпуску г -го продукта на А -м предприятии, при условии, что другие виды продукции не производятся [c.21]
Расчет /г на основании выражения (2.7) осуществляется в предположении, что выпуск какого-либо одного продукта пропорционален времени, отведенному на его производство, а суммарное время производства всех продуктов равно общему фонду времени [33]. Указанные предположения удовлетворяются приближенно, и изменения в ассортименте продукции приводят к различным погрешностям оценки Н%, а следовательно, и к различной степени соответствия аппроксимирующей гиперплоскости области производственных возможностей предприятия. [c.22]
При известных решениях прямой и двойственной задач (yk и pk) коэффициенты гиперплоскости вычисляются по формуле [c.23]
При относительной простоте аппроксимирующего выражения сама процедура построения аппроксимирующей гиперплоскости является [c.23]
В более общем случае поверхности раздела между классами можно описывать приближенно набором гиперплоскостей - но для этого уже потребуется несколько линейных дискриминаторов - нейронов. [c.52]
В /-мерном пространстве гиперплоскость может разделить произвольным образом лишь d—1 точки. Например, на плоскости можно произвольным образом разделить по двум классам три точки, но четыре - в общем случае уже невозможно (см. Рисунок 2). В случае плоскости это [c.52]
В равновесии все ценные бумаги располагаются на гиперплоскости рынка ценной бумаги, при этом на каждой оси откладывается величина вклада ценной бумаги в соответствующую характеристику эффективного портфеля, представляющую интерес для инвесторов. [c.281]
Прежде всего нужно определиться с выбором уровня сложности. В реальных ситуациях часто бывает так, что имеется лишь относительно небольшое число образцов, а структура данных позволяет выделить следующие три уровня сложности. Первый (простейший) — когда классы можно разделить прямыми линиями (или гиперплоскостями, если пространство имеет размерность больше двух). Этот случай называется линейной отделимостью. Во втором случае одной гиперплоскости для разделения недостаточно (нелинейная отдели- [c.45]
Традиционный подход к прогнозированию банкротств основан на множественном дискриминантном анализе (см. [7], [10], [12], [32], [33]). Методы такого типа используются в широко распространенных системах определения рейтинга кредитоспособности, где ищется гиперплоскость, наилучшим образом разделяющая хороших и плохих кандидатов. Хотя к настоящему времени разработано множество дискриминантных моделей, используется (в частности, в управлении кредитами) лишь небольшое число из них. В ряде случаев банки приходят к выводу, что методы MDA не дают ожидаемого улучшения точности по сравнению с традиционными методами. [c.200]
Непредсказуемость означала бы, что координаты точек временного ряда, соответствующие компонентам задержки, образуют случайное распределение вокруг гиперплоскости r(t = 0, т.е. белый шум. Если же распределение не является случайным, то при помощи нейронной сети можно аппроксимировать среднюю поверхность, отклоняющуюся от гиперплоскости r(t) = 0. [c.213]
| Рис. 10.3. Неэффективность — наличие отклонений от гиперплоскости 5=0.5 | 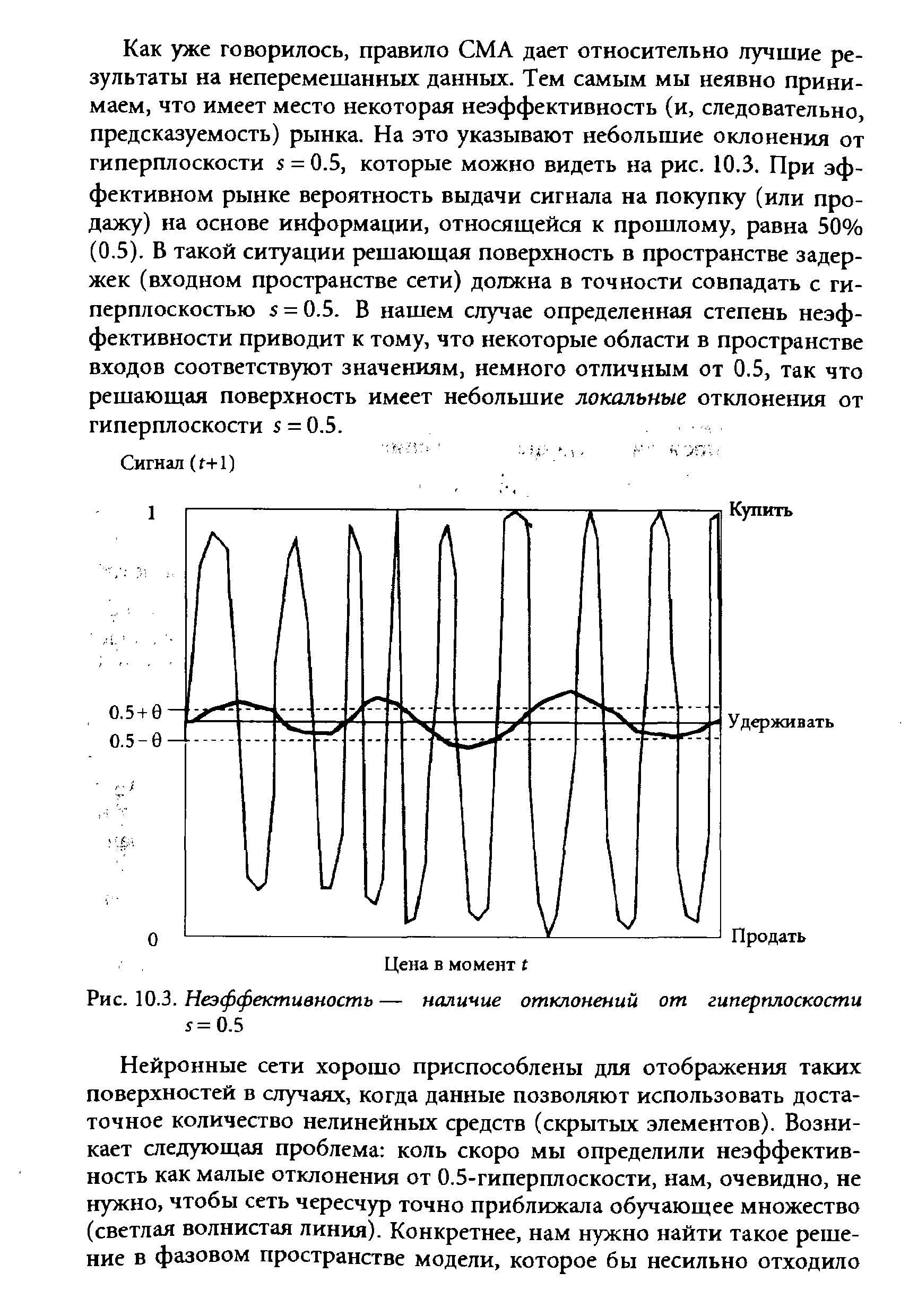 |
Этот результат, по-видимому, свидетельствует о присутствии свойств неэффективности рынка (которые определяются как малые отклонения от 0.5-гиперплоскости) и о том, что нейронная сеть является адекватным инструментом для их обнаружения. Однако необходимы дальнейшие исследования, прежде чем данный метод можно будет использовать непосредственно в торговом зале. При том, что результаты оказались многообещающими, прибыльной стратегии торговли не выработано. Мы хотим высказать ряд предложений, реализация которых, по нашему мнению, могла бы способствовать выработке более совершенной стратегии торговли. [c.227]
Формулы для расчета средних ошибок оценки положения гиперплоскости регрессии в заданной многомерной точке и для индивидуальной величины результативного признака весьма сложны, требуют применения матричной алгебры и здесь не рассматриваются. Средняя ошибка оценки значения результативного признака, рассчитанная по программе ПЭВМ Mi rostat и приведенная в табл. 8.8, равна 79,2 руб. на 1 га. Это лишь среднее квадратическое отклонение фактических значений дохода от расчетных по уравнению, не учитывающее ошибки положения самой гиперплоскости регрессии при экстраполяции значений факторных признаков. Поэтому ограничимся точечными прогнозами в нескольких вариантах (табл. 8.14). [c.289]
К недостатку аппроксимирующей гиперплоскости необходимо отнести то, что в этом случае не определяется граница допустимости подобной аппроксимации. Необходимо отметить, что применительно к нефтеперерабатывающим производствам этот недостаток частично снимается тем, что качественные показатели сырья и существующие схемы переработки нефтеперерабатывающих предприятий определяют относительную структурную устойчивость плановых решений, оцениваемых по аппроксимационным моделям. [c.20]
При моделировании нефтеперерабатывающих производств в основном используется аппроксимация в виде выпуклых многогранников. Аппроксимирующие гиперплоскости могут быть применены для описания производственных возможностей отдельных процессов и производств. Практические аспекты применения аппроксимационных моделей для решения задач планирования нефтеперерабатывающих производств были рассмотрены в разработках ЦЭМИ АН СССР [5-7]. [c.21]
Элементарной моделью аппроксимационного типа является гиперплоскость hx < 1. [c.21]
Анализируя возможные способы оценки числовых характеристик аппроксимирующих гиперплоскостей, необходимо отметить, что, практически, во всех случаях должна существовать неагрегированная модель производства, на основании которой можно рассчитать максимальные выпуски продуктов maxx , оптимальные опорные решенияyk и оценки оптимальных решений pk, или же множестве различных решений Yk и Pk, усреднением которых можно вычислить Yk uPk. Без использования экономико-математической модели, эвристическим способом приближенно могут быть определены только предельные значениях . [c.23]
Таким образом, задача идентификации объекта планирования с помощью аппроксимирующей гиперплоскости сводится к задаче построения агрегированной модели на основе информации, порождаемой неагрегированной моделью. [c.23]
Возможности линейного дискриминатора весьма ограничены. Он способен правильно решать лишь ограниченный круг задач - когда классы, подлежащие классификации линейно-разделимы, т.е. могут быть разделены гиперплоскостью (Рисунок 2). [c.52]
Как тот. так и другой набор базисных функций обеспечивают возможность аппроксимации любой непрерывной функции с произвольной точностью. Основное различие между ними в способе кодирования информации на скрытом слое. Если персепторны используют глобальные переменные (наборы бесконечных гиперплоскостей) то сети радиального базиса опираются на компактные шары, окружающие набор опорных центров (Рисунок 15). [c.86]
Если ожидаемые доходности связаны, помимо беты и ликвидности, с третьей характеристикой, то для описания соответствующего равновесия потребуется четырехмерная модель САРМ20. Хотя для такой модели нельзя нарисовать соответствующий график, для нее можно вывести соответствующее уравнение. По аналогии с трехмерным случаем его называют уравнением гиперплоскости (hyperplane). [c.281]
К сожалению, хотя теоретически характеристики нейронной сети с прямой связью стремятся к байесовской, в применении их к практическим задачам выявляется ряд недостатков. Во-первых, заранее неизвестно, какой сложности (т.е. размера) сеть потребуется для достаточно точной реализации отображения. Эта сложность может оказаться чрезмерно большой. Архитектура сети, т.е. число слоев и число элементов в каждом слое, должна быть зафиксирована до начала обучения. Эта архитектура порождает сложные нелинейные разделяющие поверхности в пространстве входов. В сети с одним скрытым слоем векторы образцов сначала преобразуются (нелинейным образом) в новое пространство представлений (пространство скрытого слоя), а затем гиперплоскости, соответствующие выходным узлам, располагаются так, чтобы разделить классы уже в этом новом пространстве. Тем самым, сеть распознает уже другие характерис- [c.46]
Настройка классификатора обычно бывает основана на пороговых правилах и/или сравнении расстояний между значениями целевых показателей. Нужно помнить, что нейронная сеть с прямой связью и сигмоидными выходами выдает ответ в непрерывном виде, обычно в интервале от 0 до 1 в зависимости от того, как располагаются разделяющие гиперплоскости скрытых элементов. Однако, даже если на выходе используются не апостериорные вероятности, а какая-либо более простая решающая функция, имеется возможность выдать надежный ответ. Настраивая критерий отбрасывания, можно [c.51]
Как уже говорилось, правило СМА дает относительно лучшие результаты на неперемешанных данных. Тем самым мы неявно принимаем, что имеет место некоторая неэффективность (и, следовательно, предсказуемость) рынка. На это указывают небольшие склонения от гиперплоскости 5 = 0.5, которые можно видеть на рис. 10.3. При эффективном рынке вероятность выдачи сигнала на покупку (или продажу) на основе информации, относящейся к прошлому, равна 50% (0.5). Б такой ситуации решающая поверхность в пространстве задержек (входном пространстве сети) должна в точности совпадать с гиперплоскостью 5 = 0.5. В нашем случае определенная степень неэффективности приводит к тому, что некоторые области в пространстве входов соответствуют значениям, немного отличным от 0.5, так что решающая поверхность имеет небольшие локальные отклонения от гиперплоскости s = 0.5. ., ..,,, [c.221]
Смотреть страницы где упоминается термин Гиперплоскость
: [c.8] [c.59] [c.19] [c.24] [c.226] [c.51] [c.53] [c.86] [c.135] [c.31] [c.59] [c.181] [c.220] [c.249] [c.50] [c.50] [c.219] [c.230]Эконометрика начальный курс (2004) -- [ c.486 ]
