В результате экстраполяции данных мы получаем точечные значения прогноза. Совпадение фактических данных будущих периодов и данных, полученных при экстраполяции, маловероятно по следующим причинам использованная при прогнозировании функция не является единственной для описания развития явления прогноз осуществлялся с использованием ограниченной информационной базы, и случайные компоненты, присущие уровням исходных данных, повлияли на результат прогноза непредвиденные события в политической и экономической жизни общества в будущем могут существенно изменить прогнозируемую тенденцию развития изучаемого показателя. [c.621]
Прогноз, полученный подстановкой в уравнение регрессии ожидаемого значения фактора, называют точечным прогнозом. Вероятность точной реализации такого прогноза крайне мала. Необходимо сопроводить его значением средней ошибки прогноза или доверительным интервалом прогноза с достаточно большой вероятностью. Средняя ошибка положения линии регрессии в генеральной совокупности при значении факторного признака, равном xh вычисляется для линии регрессии по формуле (8.20) [c.252]
Использование регрессионной модели для прогнозирования состоит в подстановке в уравнение регрессии ожидаемых значений факторных признаков для расчета точечного прогноза результативного признака или (и) его доверительного интервала с заданной вероятностью, как уже сказано в 8.2. Сформулированные там же ограничения прогнозирования по уравнению регрессии сохраняют свое значение и для многофакторных моделей. Кроме того, необходимо соблюдать системность между подставляемыми в модель значениями факторных признаков. [c.289]
Смысл прогноза в том, что при сохранении до конца 1997 г. измеренного за 1993 - 1995 гг. тренда и характера сезонных колебаний, импорт составит 50,41 млрд долл. США. Это точечный прогноз. Проблема измерения средней ошибки прогноза с учетом тренда и сезонности сложна и здесь не излагается. [c.356]
Прежде всего, вычисляется точечный прогноз - значение уровня тренда при подстановке в его уравнение номера 1998 г., считая от 1987 г., т. е. tk = 11. [c.358]
Экстраполяция дает возможность получить точечное значение прогноза. Точное совпадение фактических данных и прогностических точечных оценок, полученных путем экстраполяции кривых, характеризующих тенденцию, имеет малую вероятность. Поэтому любой статистический прогноз носит приближенный характер. В связи с этим целесообразно определение доверительных интервалов прогноза. Величина доверительного интервала определяется следующим образом [c.90]
Выше, в 3.5, 4.2, 4.5, мы рассматривали точечный и интервальный прогноз значений зависимой переменной Y, т. е. определение точечных и интервальных оценок Y, полученных для парной и множественной регрессий для значений объясняющих переменных X, расположенных вне пределов обследованного диапазона значений X. [c.144]
Пример 6.4. По данным табл. 6.1 дать точечную и с надежностью 0,95 интервальную оценки прогноза среднего и индивидуального значений спроса на некоторый товар на момент t= 9 (девятый год). (Полагаем, что тренд линейный, а возмущения удовлетворяют требованиям классической модели (см. дальше, пример 7.8.) [c.145]
Используя авторегрессионную модель 1-го порядка, дать точечный и интервальный прогноз среднего и индивидуального значений курса акций в момент t= 23, т. е. на глубину один интервал. [c.147]
Вычисления, аналогичные примеру 6.3, дают точечный прогноз по уравнению (6.13) [c.148]
Прогнозы могут быть точечными (когда результат выражается в виде одного уровня), интервальными (результат варьирует в определенных пределах) и многовариантными (результат предлагается в виде нескольких вариантов развития). Точность прогноза зависит от [c.210]
Для полученного точечного прогноза интервалы с вероятностью 0,95 будут 229,4 — 239,1, т. е. несколько вы- [c.156]
Полученные прогнозы являются точечными, и совпадение фактического значения величины (товарооборота) с прогнозируемым маловероятно. Поэтому целесообразно вычислить так называемый доверительный интервал прогноза, т. е. определить верхнюю и нижнюю границы, в которых будет находиться прогнозируемая величина. [c.32]
Доверительный i интервал зависит также от времени упреждения прогноза. С увеличением интервала между последним годом во временном ряду и годом, на который составляется прогноз, надежность точечного прогноза уменьшается, растет его неопределенность и расширяется доверительный интервал. [c.32]
Прогноз ожидаемого прироста запасов в регионе характеризуется гораздо большей неопределенностью, чем прогноз добычи из открытых месторождений. И это обстоятельство серьезно осложняет общепринятую процедуру планирования. Действительно, нелегко оперировать с неопределенностью в рамках детерминированных плановых показателей. Именно этим объясняется стремление представить прогноз ресурсов нефти и газа и ожидаемых приростов в виде точечной оценки. Однако такой подход совершенно не оправдан, поскольку невозможно сравнивать и анализировать оценки ресурсов, полученные различными методами и для разных объектов. Оценку ресурсов можно производить по шкале времени или по шкале затрат. В первом случае прогнозируется величина ресурсов, выявляемых за рассматриваемый период времени, во втором — приросты запасов на единицу затрат. Результаты таких прогнозов позволяют оценить ресурсный потенциал региона (страны), но не обеспечивают данными для построения [c.48]
Выберите лучшую форму тренда и выполните по ней точечный прогноз на 1998 г. [c.166]
На основе построенной модели дайте точечный прогноз ожидаемого потребления электроэнергии в течение первого квартала следующего года. [c.170]
На основе построенной модели дайте точечные прогнозы уровня безработицы на I и П квартал следующего года. [c.170]
Используя выбранное вами в п. 2 уравнение, дайте точечный прогноз ожидаемого значения у,-н ближайший год (период 31). [c.171]
В прогнозных расчетах по уравнению регрессии определяется предсказываемое (ур) значение как точечный прогноз ух при хр =хь т. е. путем подстановки в уравнение регрессии 5 = а + b х соответствующего значения х. Однако точечный прогноз явно не реален. Поэтому он дополняется расчетом стандартной ошибки ух, т. е. Шух, и соответственно интервальной оценкой прогнозного значения (у ) [c.57]
Чтобы ответить на этот вопрос, найдем точечный прогноз при х = 8, т. е. [c.61]
Содержательная интерпретация параметров этой модели затруднительна, однако ее можно использовать для прогнозирования. Для этого необходимо определить трендовое значение факторного признаках, и с помощью одного из методов оценить величину предполагаемого отклонения фактического значения от трендового. Далее по уравнению тренда для результативного признака определяют трендовое значение х а по уравнению регрессии по отклонениям от трендов находят величину отклонения у, — у,. Затем находят точечный прогноз фактического значения у, по формуле [c.268]
Прогноз, полученный подстановкой в уравнение регрессии ожидаемого значения фактора, называют точечным прогнозом. Вероятность точной реализации такого прогноза крайне мала. Необходимо сопроводить его значение средней ошибкой прогноза или доверительным интервалом прогноза, в который с достаточно большой вероятностью попадают прогнозные оценки. Средняя ошибка является мерой точности прогноза на основе уравнения регрессии. Существуют усовершенствованные методы парной регрессии, в какой-то степени преодолевающие его недостатки. [c.205]
Существуют три его разновидности точечный прогноз, интервальный прогноз и прогноз с вероятностным распределением. [c.205]
Точечный. Прогноз сбыта в виде конкретного количества продаж (то есть абсолютная величина без учета ошибок в ту или иную сторону). В изолированном виде точечные прогнозы - например, когда группа менеджеров категорически заявляет, что на данной территории за следующие три месяца будет продано 80 000 единиц данного продукта, — могут быть предвзяты и неточны. Следовательно, лучше иметь несколько точечных прогнозов разных групп менеджеров и составить из них один, агрегированный. [c.205]
Определение прогнозных значений на основе построенной модели. Экстраполяция выявленных тенденций (продление на будущее) позволяет получить точечный прогноз. Однако вероятность точного попадания в эту точку практически равна нулю. Отсюда следует необходимость вычисления перспективных оценок в виде "вилки" через доверительные интервалы. [c.285]
Точечный прогноз на к шагов вперед получается путем подстановки в модель параметра t — N+l,...,N+k. При прогнозировании на два шага имеем [c.293]
По способу представления результатов прогнозы подразделяются на точечные и интервальные. [c.248]
Точечный прогноз предполагает, что данный вариант включает единственное значение прогнозируемого показателя. Например, через три года будут осваиваться продуктовые инновации в электротехнике. [c.248]
| Рис. 4.S. Прогнозы а — точечный б — интервальный |  |
| Рис. 4.4. Точечный (а) и интервальный (б) прогнозы | 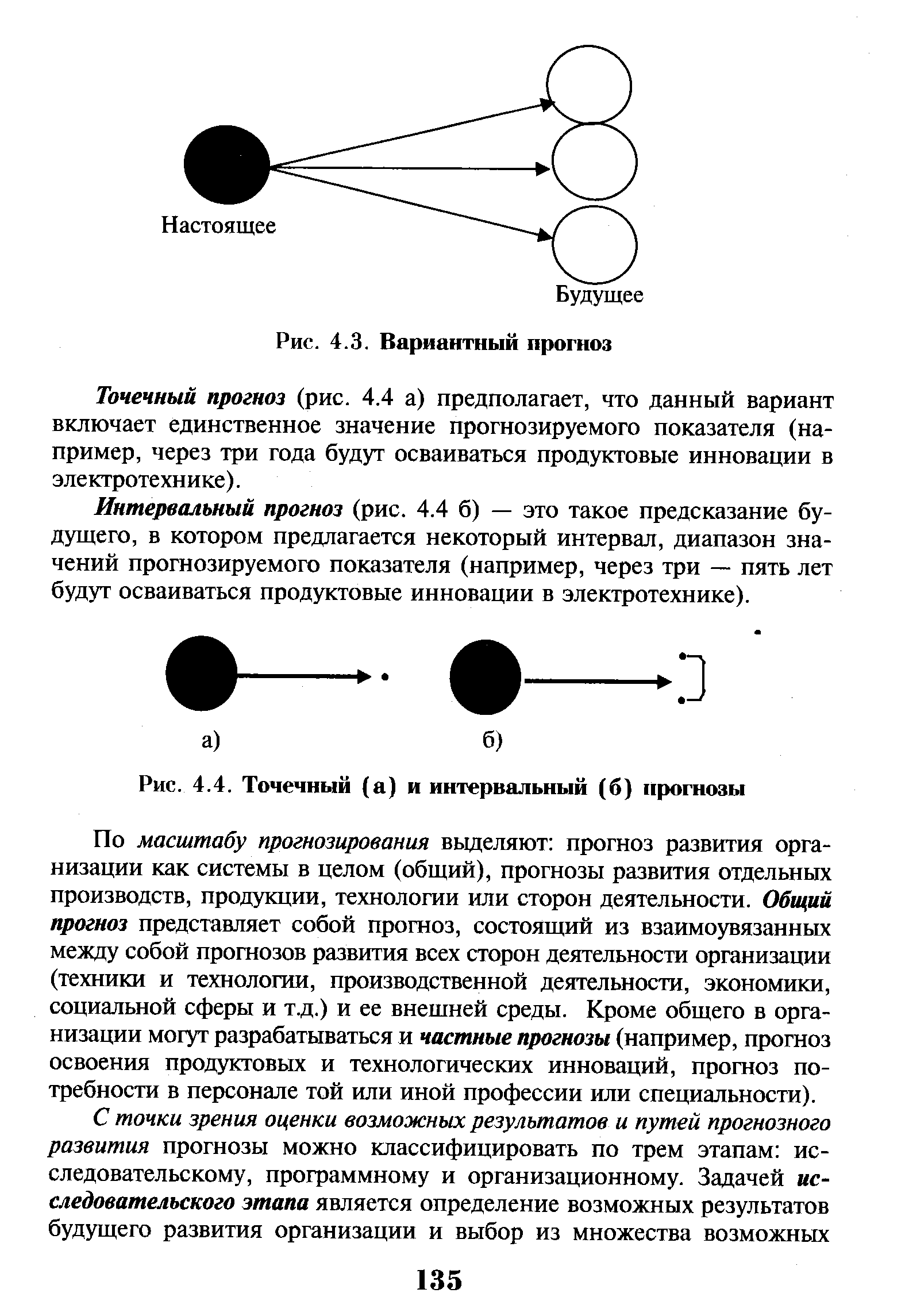 |
Типы прогнозов точечные, интервальные, многовариантные. Методы прогнозирования спроса аналоговые (эталонные, нормативные) расчеты, экстраполяция (графическая, методами сглаживания и по трен-довым моделям), использование коэффициентов эластичности, многофакторные регрессионные модели, сценарии, экспертные расчеты (Дельфи-метод). Проверка точности прогноза. [c.151]
Точечный прогноз по уравнению регрессии при среднесуточном приросте массы животных, равном 900 г, уже достигнутом передовыми хозяйствами, приводит к ожидаемой средней себес- [c.268]
Формулы для расчета средних ошибок оценки положения гиперплоскости регрессии в заданной многомерной точке и для индивидуальной величины результативного признака весьма сложны, требуют применения матричной алгебры и здесь не рассматриваются. Средняя ошибка оценки значения результативного признака, рассчитанная по программе ПЭВМ Mi rostat и приведенная в табл. 8.8, равна 79,2 руб. на 1 га. Это лишь среднее квадратическое отклонение фактических значений дохода от расчетных по уравнению, не учитывающее ошибки положения самой гиперплоскости регрессии при экстраполяции значений факторных признаков. Поэтому ограничимся точечными прогнозами в нескольких вариантах (табл. 8.14). [c.289]
Но интервалы, в которых должна находиться прогнозируемая величина (точечный прогноз), оказываются для авторсгрессиоиных схем более широкими ввиду существенно большей величины среднего квадратического отклонения по сравнению с отклонением при простой экстраполяции (2, 43, см. г бл. 2), что означает большую колеблемость. Поэтому приходится прийти к заключению, что применение авторегресснопных схем в данном случае не дает результатов намного лучших, чем построение подходящего уравнения регрессии по времени. [c.158]
По данным о валовом товарообороте Главнефтеснаба РСФСР за период с 1960 по 1975 г. рассчитаны точечные и интервальные прогнозы на 1975 и 1980 гг. по прямой и экспо- [c.34]
ТОЧЕЧНЫЙ ПРОГНОЗ [point predi tion] — прогноз, которым указывается единственное значение прогнозируемого показателя. Пример "население города N в 2010 г. достигнет 35 тыс. человек". Ср. Интервальный прогноз. [c.365]
