Ее отличие от первого варианта связано со значением Х0=0, что приводит к существенной погрешности аппроксимации (6). Дело в том, что точность (6) предполагает наличие у функции непрерывной первой производной. В случае задачи с Х0 > 0 искомое решение, как известно, обладает необходимым запасом гладкости. Однако при Х0=0 оно имеет особенность при t=0 типа Jt, что дает в производной бесконечность типа t 4. Это приводит к полному искажению численного решения. В самом деле, рассмотрим сеточную функцию следующего вида [c.224]
Эта модель легко интерпретировалась с точки зрения экономического содержания. Действительно, х(1> и х(2) являются ведущими аргументами, увеличение которых положительно сказывается на выработке, а (3) — это производство продукции внутри треста, которое в силу малой мощности предприятий не может быть рентабельным, но без него невозможно строительство. Погрешность аппроксимации в терминах е — среднего абсолютного относительного отклонения и а — стандартного отклонения составила для (10.4) [c.322]
Анализ точности регрессионной модели в рамках реалистической схемы сводится к вычислению оценки о для средне-квадратической погрешности аппроксимации о по обычной формуле выборочной остаточной дисперсии. Однако остатки [c.361]
При оптимизации для продуктов 12 и 17 получился меньший вклад в покрытие, чем в исходном варианте, что связано с погрешностью аппроксимации данных региональных менеджеров, йом случае рекомендуется выбирать объемы и цены, дающие максимальный вклад в покрытие по данным предприятия. [c.393]
Следует отметить, что при всей своей очевидной сложности, вычисление IRR по вышеописанной методике дает лишь приблизительные результаты это связано с тем, что в расчетах взаимосвязь NPV и ставки дисконтирования полагается линейной, в то время как в действительности она таковой не является (как показано на рис. 10.1). Более того, погрешность в данном случае зависит и от разницы выбранных процентных ставок чем она больше, тем менее точной будет наша оценка IRR. Это продемонстрировано на рис. 10.2 линия АВ представляет собой линейную аппроксимацию взаимосвязи NPV и ставки дисконтирования, основанную на значениях ставки 15 и 25 %, а линия АС — линейную аппроксимацию той же взаимосвязи, при значениях ставки 15 и 50 %. Как видно из рис. 10.2, разрыв между двумя ставками увеличивается, и оценка IRR сдвигается вправо (т.е. увеличивается). [c.458]
Если шаг в модели затрат достаточно широк, то так называемые пошагово-переменные затраты могут становиться "пошагово-постоянными" или даже постоянными затратами. На рис. 10.6 показаны затраты труда как переменные, при этом допущена небольшая погрешность, вызванная выравниванием функции. На рис. 10.7 затраты на выполнение контрольных функций имеют широкий шаг, такой, что постоянно-затратная аппроксимация будет более точна, чем переменно-затратная в пределах релевантной области. [c.239]
Результаты решений по различным интервалам аппроксимации (см. табл. 86) могут быть отнесены в одну группу по значениям функционалов, различающихся не более чем на 2—3%. Если этот процент считать соизмеримым с погрешностью определения нормативов, то в качестве решения нелинейной задачи можно принять оптимальный план любого интервала, отвечающего максимальным значениям функционалов (с принятой точностью). Это позволяет выбрать такой план, реализация которого на месторождении была бы наиболее целесообразна, например вместо пикового разбуривания месторождения — плановое (распределенное по годам периода разбуривания). [c.228]
Чем меньше теоретическая линия регрессии (рассчитанная по уравнению) отклоняется от фактической (эмпиричной), тем меньше средняя ошибка аппроксимации. В нашем примере она составляет 0,0364, или 3,64 %. Учитывая, что в экономических расчетах допускается погрешность 5-8 %, можно сделать вывод, что исследуемое уравнение связи довольно точно описывает изучаемые зависимости. [c.152]
Количество одновременно выполняемых операций колеблется в пределах от 120 (умножение переменной на постоянный коэффициент больше единицы) до 2 (воспроизведение специальных функций). Погрешность вычислений 0—0,8%. Максимальное значение погрешностей приходится на воспроизведение тригонометрических функций и на воспроизведение нелинейных функций методом кусочно-линейной аппроксимации (от 0,5 до 0,8%). [c.130]
Подобное соотношение выполняется уже после нескольких первых итераций, однако в целом управление еще не оптимально. Знак ">о W+g"7 ( ) становится на ( , а), по существу, случайной величиной, зависящей, в частности, и от погрешностей конечно-разностной аппроксимации дифференциальных уравнений. Следовательно, и u (t) на (tlt t2) становится, в известной мере, случайной. В сочетании с некорректностью задачи эта случайность и приводит [c.350]
Этап 7 (анализ точности полученных уравнений связи). Исследователь должен отдавать себе отчет в том, что найденная им в соответствии с (В.24) аппроксимация f (X) неизвестной теоретической функции fT (X) из соотношений типа (В. 14), (В. 16) или (В.21) (называемая эмпирической функцией регрессии, см. гл. 5) является лишь некоторым приближением истинной зависимости fT (X)1. При этом погрешность в описании неизвестной истинной функции fT (X) с помощью f (X) в общем случае состоит из двух составляющих а) ошибки аппроксимации 6F и б) ошибки выборки б (/г). Величина первой зависит от успеха в реализации этапа 4, т. е. от правильности выбора класса допустимых решений F. В частности, если класс F выбран таким образом, что включает в себя и неизвестную истинную функцию f (т. е. fT (X) F), то ошибка аппроксимации 6F = 0. Но даже в этом случае остается случайная составляющая (ошибка выборки) б (/г), обусловленная ограниченностью выборочных данных вида (В.1), па основании которых мы подбираем функцию f (X) (оцениваем ее параметры). Очевидно, уменьшить ошибку выборки мы можем за счет увеличения объема п обрабатываемых выборочных данных, так как при fT (X) F (т. е. при 6F — 0) и правильно выбранных методах статистического оценивания (т. е. при правильном выборе оптимизируемого функционала качества модели Дп (/)) ошибка выборки б (/г) -> 0 (по вероятности) при п — оо (свойство состоятельности используемой процедуры статистического оценивания неизвестной функции fT (X)). [c.52]
По рисунку видно, что при использовании неадекватной параметрической модели погрешность наибольшая. Локальная параболическая аппроксимация с использованием полинома второй степени лучше, чем традиционно применяемая аппроксимация полиномом нулевой степени. Первая не только дает наименьшую погрешность, но и значительно устойчивее к выбору величины Ь. [c.323]
| Рис. 10.1. Зависимость погрешности локальной параболической аппроксимации от величины b для выборки объема а) п = 75 б) л = | 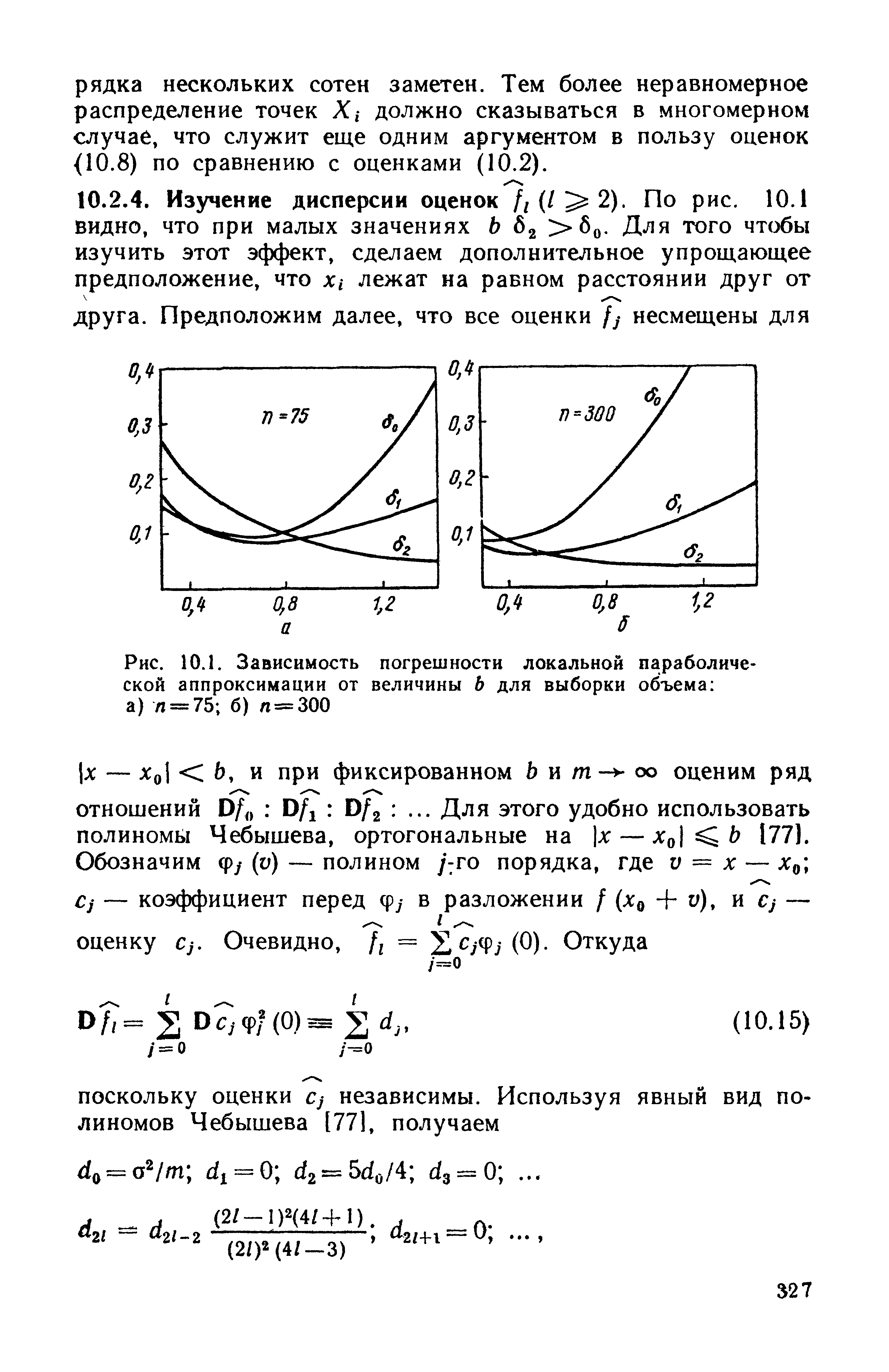 |
Для удобства дальнейшего использования (например, при вычислениях интервальных оценок погрешностей) эмпирическую плотность распределения, представленную гистограммой, аппроксимируют непрерывной аналитической функцией. Как правило, при этом для аппроксимации стараются подобрать аналитические выражения, характерные для определенных теоретических (вероятностных) распределений. [c.52]
Для оценки точности уравнения связи рассчитывается средняя ошибка аппроксимации. Чем меньше теоретическая линия регрессии (рассчитанная по уравнению) отклоняется от фактической (эмпирической), тем меньше ее величина. А это свидетельствует о правильности подбора формы уравнения связи. В нашем примере она составляет 0,0364, или 3,64 %. Учитывая, что в экономических расчетах допускаемая погрешность находится в пределах 5—8 %, можно сделать вы- [c.47]
Чем меньше теоретическая линия регрессии (рассчитанная по уравнению) отклоняется от фактической (эмпирической), тем меньше средняя ошибка аппроксимации, а это свидетельствует о правильности подбора формы уравнения связи. В нашем примере она составляет 0,0364, или 3,64%. Учитывая, что в экономических расчетах допускается погрешность 5—8%, можно сделать вывод, что данное уравнение связи довольно точно описывает изучаемые зависимости. С такой же небольшой погрешностью будет делаться и прогноз уровня рентабельности по данному уравнению. [c.144]
Основные данные установки максимальный порядок решаемых систем дифференциальных уравнений—12—16-й погрешность задания постоянных коэффициентов—0,5% погрешность воспроизведения переменных коэффициентов (без учета погрешности аппроксимации)— 0,5% погрешность интегрирования входного сигнала — 0,5% дрейф усилителя в режиме интегрирования — за 100 сек 40—50 мв фоновая составляющая усилителя при коэффициенте усилителя, равном 1, составляет 20 мв погрешность решения систем дифференциальных уравнений до 12-го порядка — 5—10% с частотой свободных колебаний до 8 гц. Питание — от однофазной сети переменного тока напряжением 220 в, частотой 50 гц потребляемая мощность — 6 ква. При питании от трехфазной сети переменного тока напряжением 380/220 или. 220/127 в, частотой 50 гц по ребляемая мощность —0,8 ква. Габаритные размеры установки (без блоков питания) 5400x500X1230 мм габаритные размеры секций СУ, СОУ-2 и СПК-2 622X476X1230 мм тзес установки — 1246 кг. [c.128]
В экономической практике и исследованиях вычислительная привлекательность-и хорошая интерпретируемость линейных моделей (не обязательно оптимизационных, т.е. моделей в широком смысле) делает целесообразным их применение и в случае линейной аппроксимации с приемлемой погрешностью нелинейных закономерностей, если это не мешает экономическому содержанию задачи. [c.65]
На рис. ЮЛ показаны значения 6 (/ — О, 1, 2), соответствующие непараметрическому оцениванию с помощью метода локальной параболической (порядка i) аппроксимации ( 10.2) с весовой функцией w (х, х0) = ехр — (х — х0)2/2Ь2 . Параметрическое оценивание с неадекватно предположенной моделью /пар — (а + сх) 1 в обоих случаях (п — 75 и п = 300) дало значительно большую погрешность 8пар>1. [c.323]
Такая аппроксимация позволяет получать дисперсии dqi с погрешностью, находящейся в пределах 15 % даже при эрланговских потоках и постоянных временах обслуживания. Однако при перегрузках (при значениях рД существенно больших 0 и близких к 1) это выражение становится практически точным, и можно показать, что распределение числа заявок в очереди при перегрузке - экспоненциальное, Поэтому дисперсия времени пребывания в очереди равна [c.52]
Напомним (см. с. 55 ), что приведенные на этом графике значения k являются средними для класса усеченных, симметричных и одномодальных распределений погрешности, т.е. в тех случаях, когда о кривой плотности распределения погрешности известно, что она является усеченной, симметричной и одномодальной, и другие данные отсутствуют, использование k p обеспечивает наибольшую точность оценок интервальных характеристик погрешности. Максимальные погрешности значений k, обусловленные отличием реальных законов распределения от принятой (средней) аппроксимации, для которой получены эти (k ) коэффициенты, приведены на том же графике (см. рис. 7). [c.152]
Хотя сцепленные индексы, построенные на основе почти всех используемых на практике индексных формул, и являются аппроксимациями индексов Дивизиа, скорость сходимости последовательности сцепленных индексов к индексу Дивизиа с уменьшением шага по времени до нуля существенно зависит от выбора индексной формулы. Так, при г— 0 погрешность сцепленного индекса Ласпейреса равна О(т) и аналогично для сцепленного индекса Пааше. Поэтому эти методы являются методами первого порядка, т.е. соответствующие сцепленные индексы достаточно медленно сходятся к индексу Дивизиа. Сцепленные индексы Фишера, Эджворта-Маршалла, Торнквиста являются методами второго порядка, поскольку при уменьшении шага по времени г погрешность этих методов равна О(т ), т.е. они, вообще говоря, сходятся к индексу Дивизиа гораздо быстрее, чем сцепленные индексы Ласпейреса и Пааше34. [c.41]
Комплексные сценарии, включающие в себя изменения волатильностей и корреляций, используются при стресс-тестировании показателя VaR (stressing VaR), которое иногда выделяют в самостоятельную разновидность стресс-тестирования. Согласно распространенным рекомендациям, при расчете VaR ковариационным методом или методом Монте-Карло стресс-тестирование следует проводить, варьируя в различных комбинациях входные параметры — волатильности и корреляции. Однако не следует забывать, что дельта-нормальный метод расчета VaR основан на линейной аппроксимации чувствительности цен инструментов к относительно небольшим (в пределе — к бесконечно малым) изменениям факторов риска . Для инструментов с нелинейными функциями ценообразования погрешность такого приближения будет тем больше, чем сильнее реальное изменение фактора риска отличается от того, которое предполагалось при оценке чувствительности. В случае стресс-тестирования речь идет именно о внезапных и очень больших по величине скачках факторов риска, поэтому необходимо либо специально оценивать линейную чувствительность к изменениям такого масштаба, либо проводить стресс-тестирование только корреляционной, а не ковариационной матрицы. [c.595]
