Мы начнем изучение процесса принятия подобных решений с простой модели дуополии (две фирмы конкурируют друг с другом), впервые представленной французским экономистом О. Курно в 1838 г. Предположим, фирмы производят однородный товар и знают кривую рыночного спроса. Каждая фирма должна решить, сколько продукции выпускать, и обе фирмы принимают свои решения в одно и то же время. При принятии производственных решений каждая фирма должна помнить, что ее конкурент тоже принимает решение по объему производства и что конечная цена будет зависеть от совокупного объема производства обеих фирм. [c.347]
МОДЕЛЬ ДУОПОЛИИ КУРНО [c.159]
Модель дуополии по Курно [c.59]
Рассмотрим модель дуополии по Курно с функцией [c.80]
В нашей модели дуополии по Курно, как уже отмечалось, [c.135]
Модель дуополии обладает большой наглядностью, но определение равновесия Курно легко обобщается на случай олигополии с произвольным числом фирм. Пусть Q, — объем продукта i-той фирмы. [c.627]
Отметим, что в классической модели дуополии Курно предполагается, что Зжг/Зж = о и 9zi/9z2 = О, т. е. стороны принимают решения об объеме выпуска без учета действий соперника и без процесса обучения. (Прим. ред.). [c.345]
МОДЕЛЬ ДУОПОЛИИ КУРНО — [c.382]
Модель дуополии Курно 382 [c.794]
Точка пересечения кривых реагирования определяет равновесие по Курно, т. е. равновесие по Нэшу в модели дуополии по Курно. [c.50]
Рассмотрим следующий конечный вариант модели дуополии по Курно. Допустим, что каждая из фирм должна выбрать, производить ли половину монопольного объема продукции, gm/2 = (а — с)/4, либо равновесный по Курно объем, q = (а — с)/3. Другие объемы производства в такой модели невозможны. Показать, что эта игра с двумя ходами эквивалентна дилемме Заключенного каждая фирма имеет строго доминируемую стратегию и в равновесии обе фирмы оказываются в менее выгодном положении, нежели в ситуации, когда бы они выбрали сотрудничество (кооперацию). [c.79]
В нашей модели дуополии по Курно, как уже отмечалось, стратегия игрока 2 — это пара (q ( н), q ( L)) [c.126]
Политика установления уровня производства модель дуополии Курно. [c.245]
Простейшую модель дуополии Курно можно развить и представить её в более общем виде для олигополистического рынка с любым конечным числом фирм. [c.248]
Модель дуополии Курно [c.140]
Каждый производитель стремится максимизировать свою прибыль и предполагает, что выпуск его конкурента будет неизменен. Тогда модель дуополии Курно в общем виде можно представить так [c.140]
Вопрос об устойчивости равновесия Курно в общем случае решается значительно сложнее, чем для дуополии. При большом числе фирм условия устойчивости равновесия Курно в пределе совпадают с условием устойчивости паутинообразной модели (см. лекцию 9). [c.627]
Если фирмы устанавливают объем производства или уровень мощностей (модель Курно), объем производства при дуополии выше, чем при монополии, и ниже, чем при совершенной конкуренции. Аналогично, цена при дуополии ниже, чем при монополии, и выше, чем при совершенной конкуренции. [c.129]
Анализируя модель Курно, мы рассматривали простейший случай дуополии. А что происходит, когда фирм больше, чем две Один из подходов к общему случаю олигополии — повторить графический анализ главы 7, но с введением в моделируемую ситуацию более двух фирм. [c.155]
Модель Курно показывает, каким образом на рынке дуополии (двух продавцов) устанавливаются цена и выпуск одного и того же вида продукции. Модель строится на предположении, что каждый из участников определяет для себя объем производства исходя из объема предложения конкурента. При этом отыскивается рыночное, равновесие объемов производств, которое устраивает каждого и не стимулирует их к изменению своих позиции на рынке. Обе фирмы борются за свою долю в рынке, сбивая цены и уменьшая тем самым предельный доход конкурента. Такое противоборство выгодно до тех пор, пока увеличение производства компенсирует потери от снижения цены. При достижении подобных параметров фирма попадает в состояние экономического равновесия. Аналогичная ситуация складывается и у конкурента. Графически эта мысль отображена на рис. 8.11. [c.153]
| Рис. 15.4. Равновесие дуополии в модели Курно | 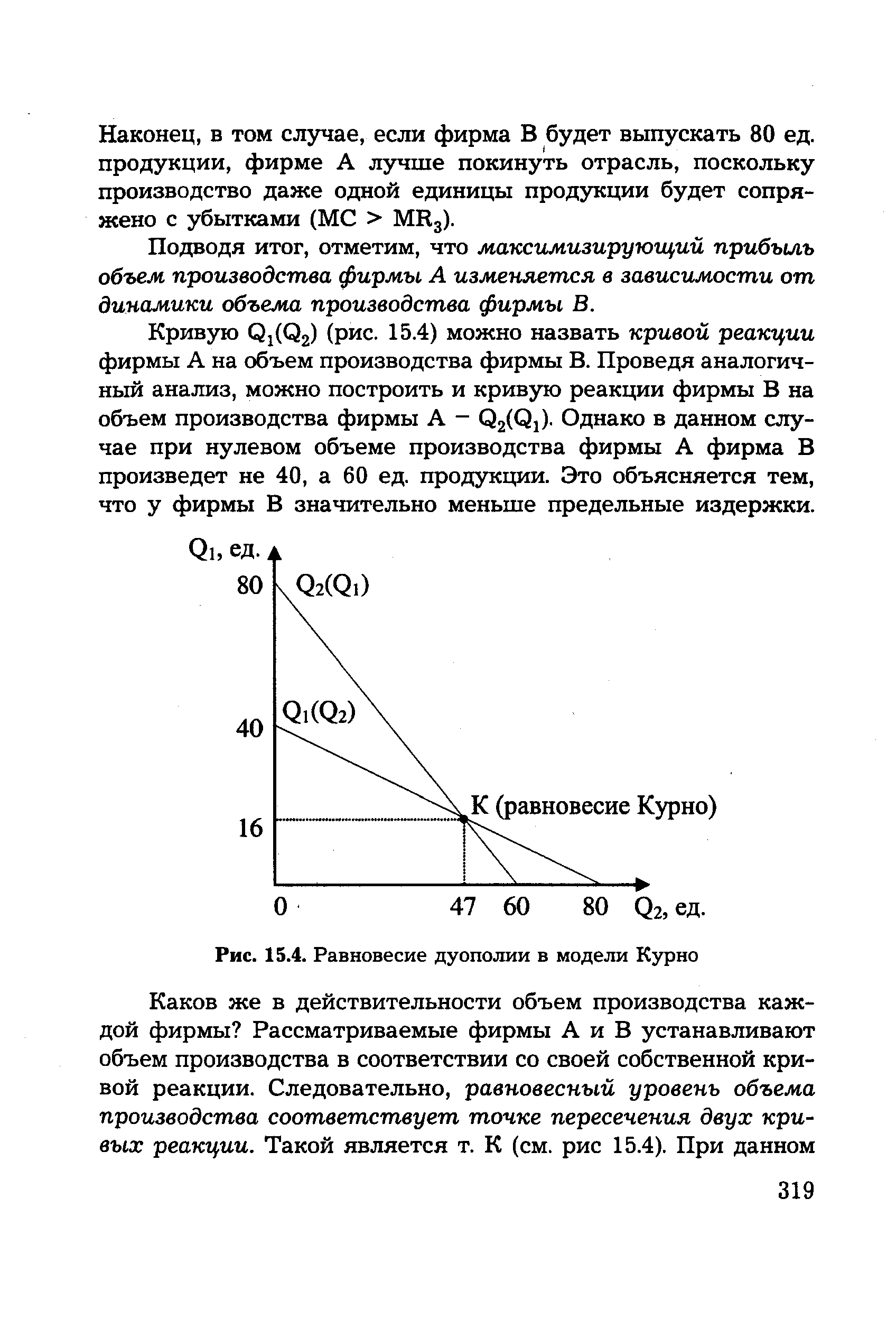 |
Дуополию такого вида можно изобразить на диаграмме, аналогичной Рис. 112 для дуополии Курно. Только по осям должны стоять не объемы производства, а цены, и кривые равной прибыли будут развернуты в противоположную сторону. Равновесием будет точка пересечения кривых отклика (см. Рис. 120). Вообще, аналогия с моделью Курно очень [c.559]
Об экономико-математических моделях конкуренции см. Курно модель дуополии, Лернера коэффициент, Оли-гопольиые эксперименты, Стэкельбер-га модель дуополии, Теория игр см. также Естественная монополия, Монополия, Монопольная власть, Монополистическая конкуренция, Монопсония, Олигополия, Рынок, Рыночная цена. [c.151]
КУРНО МОДЕЛЬ ДУОПОЛИИ [ ournot duopoly model] — простая модель олигополии (на примере ее частного случая — дуополии), где фирмы конкурируют друг с другом, производя однородный товар и зная общую кривую рыночного спроса. [c.165]
Пример равновесия по Нэшу см. в ст. "Курно модель дуополии". (См. также Бескоалиционные игры, Некоопера-тивиые игры, Оптимум по Парето, Эд-жуорта диаграмма.) [c.231]
Первая модель дуополии была предложена французским экономистом А. Курно еще в 1838 г. она подробно рассматривается в статье Игровая модель олигополии Математического приложения. Центральным моментом теории Курно явилось понятие равновесия на дуополистическом рынке. Под равновесным понимается такое сочетание объемов выпуска каждой из фирм, при котором ни у одной из них нет стимулов для изменения своего решения прибыль каждой фирмы максимальна при условии, что конкурент сохранит данный объем выпуска (равновесие Курно). [c.195]
Модель дуополии обладает большой наглядностью, но определение равновесия Курно легко обобщается на случай олигополии с произвольным числом фирм. Пусть Qi — объем продукта г -й фирмы. Q = Qi — совокупный объем продукта всех фирм. Введем в рассмо- [c.247]
Рассмотрим модель дуополии по Курно с функцией обратного спроса P(Q) = а — Q. Будем считать, что фирмы имеют ассимметричные предельные затраты с для 7-ой фирмы и с-2 /7-ой фирмы. Что будет являться равновесием по Нэшу, если 0 < сг- < а/2 для каждой фирмы Что если с < с2 < а, но 2с2 > а + GI [c.80]
Две модели дуополистической конкуренции, представленные в предыдущих параграфах, имеют схожие посылки, но резко контрастируют по выводам. Согласно модели Курно, цена в условиях дуополии ниже монопольной цены, но выше цены в условиях совершенной конкуренции. Согласно же модели Бертрана, дуополистической конкуренции достаточно для того, чтобы снизить цены до уровня предельных издержек, т.е. двух фирм хватает, чтобы установить цены на уровне совершенной конкуренции. [c.118]
II учебных курсах изучаются основные модели олигополии, такие, как дуополия Курно—Нэша, модель лидера и последователя Стэкклберга, открытый картель, ломаная кривая спроса. В 70—80-е гг. особую популярность приобрели модели, построенные на основе теории игр игры с нуле-imii суммой, демонстрирующие закономерности стратегии жесткого вза- [c.369]
Этот подход столь же почтенен, как и сам равновесный анализ исследование Курно дуополии ( ournot, 1838) по существу "явило миру" и равновесие по Нэшу, и специфический процесс обучения (см. раздел 1.9). Курно исходил из того, что в каждом "раунде" каждая фирма выбирает объемы производства, которые максимизируют ее прибыль в предположении ("гипотеза Курно"), что конкурент продолжает выпускать тот же объем продукции, что и в предыдущем раунде. Называемая теперь "динамикой лучшего ответа", эта динамика до сих пор привлекает внимание как одна из моделей обучения в играх (Bernheim (1984), Moulin (1986)). В то же время представляется неразумным предполагать, что реальные фирмы будут вести себя таким специфическим образом, как это описано у Курно. Это относится к си- [c.170]
