Дуополию Штакельберга можно представить графически (см. Рис. 114). Разницу между равновесиями в моделях Курно и Штакельберга иллюстрирует Рисунок 115. Лидер выбирает точку на кривой отклика, которая бы максимизировала его прибыль. В равновесии кривая равной прибыли лидера касается кривой отклика. [c.541]
Функция R2(- убывает, например, в случае линейного спроса и постоянных предельных издержек. Пример возрастающей функции отклика построить достаточно трудно. На Рис. 116 показана кривая отклика, соответствующая обратной функции спроса р(у) = 1/у2 при постоянных предельных издержках. При малых объемах производства лидера она возрастает, а при больших — убывает. Для более общего случая рассмотрим теорему. [c.544]
Иллюстрация полученных соотношений для случая убывающей кривой отклика представлена на Рис. 117. Из рисунка видно, что поскольку точка равновесия в модели Штакельберга лежит ниже кривой равной прибыли, проходящей через точка равновесия в модели Курно, то объем у2 должен быть выше у2. Из-за убывания функции отклика объем yi ока- [c.545]
Две фирмы, конкурируя на рынке, выбирают объемы производства. Известно, что для этих фирм равновесный объем производства в модели Курно совпадает с равновесным объемом производства в модели Штакельберга. Каков наклон кривых отклика в этой общей точке равновесия Пояснить графически с использованием кривых отклика и кривых равной прибыли. [c.547]
Проиллюстрировать ситуацию и показать, что олигополия Курно выпускает больше оптимального количества продукции (с точки зрения ее участников) для случая дуополии можно графически (Рис. 118). Поскольку, в любой точке любой кривой отклика касательная к кривой равной прибыли параллельны осям, то в точке равновесия Курно касательные к кривым равной прибыли перпендикулярны друг другу, и поэтому возможен сдвиг, который увеличивает прибыль обоих олигополистов (на рисунке показан стрелкой). [c.549]
Дуополию такого вида можно изобразить на диаграмме, аналогичной Рис. 112 для дуополии Курно. Только по осям должны стоять не объемы производства, а цены, и кривые равной прибыли будут развернуты в противоположную сторону. Равновесием будет точка пересечения кривых отклика (см. Рис. 120). Вообще, аналогия с моделью Курно очень [c.559]
| Рис. 20. Кривые отклика при отсутствии взаимодействия | 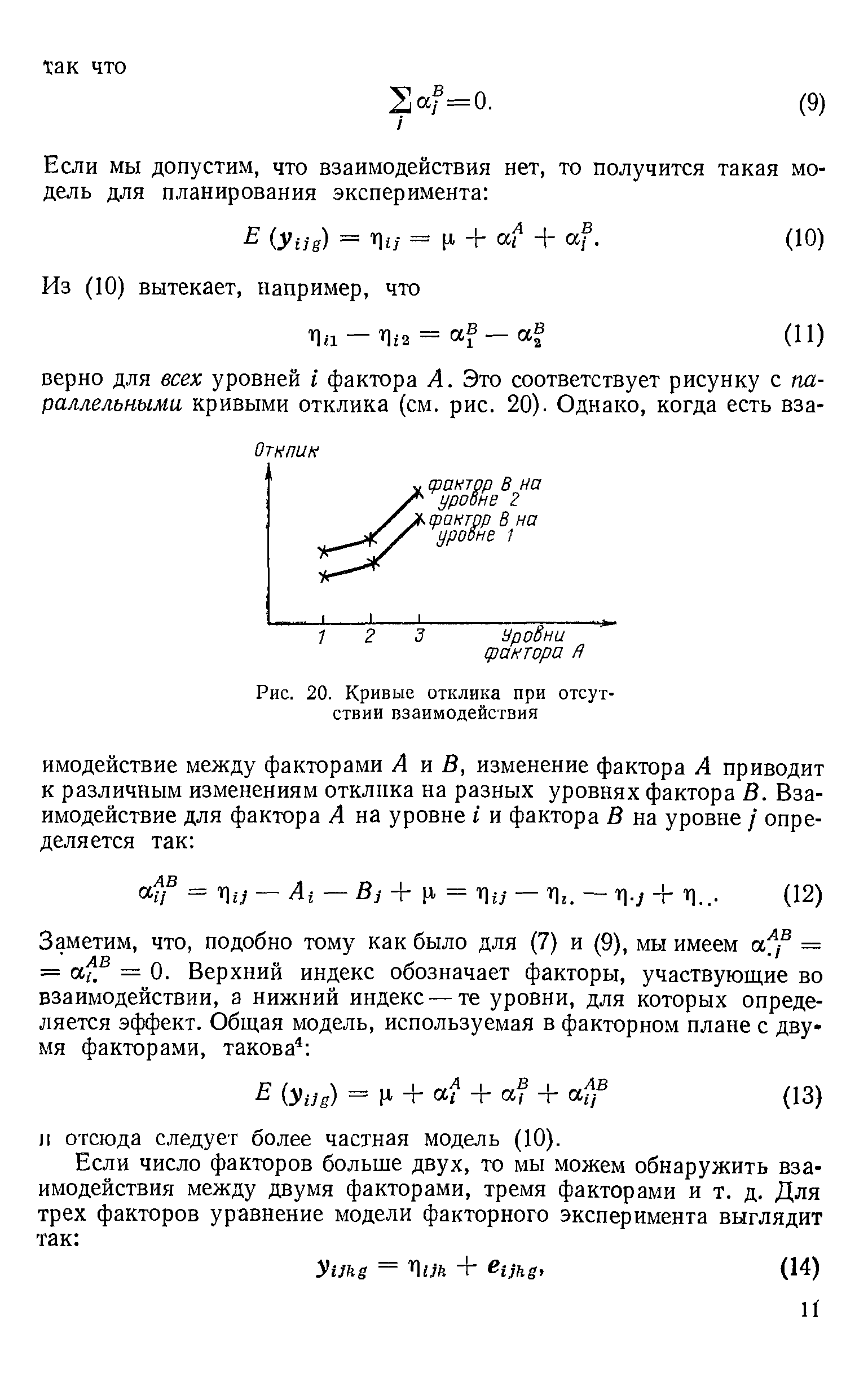 |
Поясним это утверждение на простом примере. Пусть наша задача состоит в том, чтобы описать кривую зависимости цены бескупонной облигации от срока до погашения облигации. В данном случае фактором X является срок до погашения, откликом 7 является цена. На эту математическую модель можно наложить очевидные ограничения [c.103]
Логистическая кривая имеет вид положенной на бок латинской буквы S. Она описывает случай когда при увеличении фактора X отклик 7 изменяется (снижается при а > О или растет при а < О ) в пределах от 0 до 1. При этом изменения происходят при х < b с увеличивающейся скоростью и при X > b с уменьшающейся скоростью. Преобразование данных [c.129]
Рыночная кривая предложения наклонена менее круто, чем кривые отдельных продавцов, поскольку рынок откликается на повышение цены большим абсолютным увеличением объема предложения. [c.94]
Рассмотрим метод крутого восхождения при определении градиента по линейному приближению поверхности отклика, полученному на основе факторного эксперимента. На рис. 7.6 нанесены кривые равного уровня поверхности отклика для двух независимых переменных. Если построить нормали к кривым равного уровня, то получим направления градиента. Движение из точки О в направлении ОР - это наиболее крутой путь подъема по поверхности отклика. В направлении ОР исследователь будет двигаться до тех пор, пока не перейдет точку Q. В окрестности точки Q надо будет поставить новую серию опытов и заново найти направление градиента (QM). [c.270]
Основной смысл попыток по количественной оценке всех этих параметров заключается не столько в том, чтобы выявить конкретные значения некоторого "универсального" параметра, сколько в том, чтобы проиллюстрировать те подходы, которые могут использоваться для оценки соответствующих функций в контексте рассматриваемого вопроса. Более того, следует обязательно помнить и то, что параметры функций отклика и затухания с большой степенью вероятности зависят также и от того, какой именно показатель эффективности рекламы изучается в данном случае, скорее всего, кривые, характеризующие степень узнавания, запоминаемости и отношение к предмету рекламы, будут отличаться друг от друга. Мы намного больше знаем о запоминаемости рекламы, чем о характеристиках узнаваемости или признаках формирования отношения к рекламе, хотя есть веские основания полагать, что с течением времени два последних показателя будут затухать менее интенсивно, чем это было установлено для уровня запоминаемости [52]. [c.635]
На своих семинарах я постоянно прослеживаю кривую жизненного цикла почтового отправления. Мы называем поле, расположенное над пороговым уровнем реакции, видимым результатом кампании директ маркетинга . Пространство, расположенное ниже линии проявившихся реакций, мы именуем невидимым действием кампании ДМ . Так, после каждой прямой рассылки почтовых отправлений степень известности вашей марки или продукта возрастает даже в том случае, если вы не ощущаете почти никакой реакции. Прежде чем человек что-то выбросит в мусорное ведро, он обязательно посмотрит, что он собирается выбрасывать. В результате у него остаются положительные или отрицательные воспоминания о вашем послании. То же самое касается мнения о вашем продукте или вашей фирме. Имидж ваших продукта или фирмы в глазах получателей прямых почтовых отправлений может меняться в положительную или отрицательную сторону. Риск изменения мнения о вашем продукте или фирме в отрицательную сторону велик, если видимым результатом кампании будет небольшое количество откликов. Увеличение степени известности фирмы и выпускаемых ею продуктов, а также улучшение их имиджа являются целями классической рекламы. [c.11]
Проиллюстрировать ситуацию и показать, что такая олигополия выпускает больше Парето-оптимального количества продукции (с точки зрения ее участников) для случая дуополии можно графически (Рис.3 б). На рисунке изображены кривые постоянной прибыли (7Ti(2/i,2/2) = onst и тг2(2/1,2/2) = onst) и кривые отклика (у = У (уъ) и 2/2 = ЗМш))- которые можно определить как множество точек, где касательные к кривым равной прибыли параллельны соответствующим осям координат. Точка пересечения кривых отклика является равновесием Нэша-Курно (yN). Поскольку, как и везде, в точке равновесия касательные к кривым равной прибыли перпендикулярны друг другу, значит, возможен Парето -улучшающий сдвиг (на рисунке показан стрелкой). [c.49]
Проиллюстрируем с помощью графика равновесие Курно для случая двух фирм (дуополии) (Рис. 112). На рисунке изображены кривые постоянной прибыли (П у ) = onst и П2( /1, г/2) = onst) и кривые отклика (yl= Ri(y2) и у2= -R2(yJ), которые можно определить как множество точек, где касательные к кривым равной прибыли параллельны соответствующим осям координат. Точка пересечения кривых отклика является равновесием Нэша-Курно (у ). [c.520]
Графически поиск равновесия Нэша показан не Рис. 152. Точки, лежащие на кривых оптимального отклика т Тз) и ( i) характеризуются тем, что в них касательные к кривым безразличия игроков параллельны соответствующей оси координат. Напомним, что кривой безразличия называют множество точек, в которых полезность рассматриваемого индивидуума одна и та же (иг(х) = onst). Равновесие находится как точка пересечения кривых отклика. [c.640]
Предположение о том, что объем сбыта продукции определяется исключительно расходами на рекламу, изначально неправомерно практически во всех ситуациях. На форму этой кривой всегда оказывают влияние также характер проводимой рекламной кампании, применяемые при этом рекламные тексты и выбор конкретных носителей рекламы. Очевидно, что реакция потенциальных покупателей на изобретательный и запоминающийся рекламный ролик будет совсем иной, чем отклик на безвкусную и нецеленаправленную рекламную кампанию даже при одинаковых рекламных бюджетах. Исследования, проведенные компанией ampbell Soup ompany и фирмой IRI, показали, что наибольшие изменения в объемах сбыта продукции происходят вовсе не вследствие изменения объема средств, которые фирма тратит на рекламу. Чаще всего на объем сбыта влияет то, каким именно образом фирма тратит эти средства — т.е. каким образом она проводит выбор целевых рынков и рекламных носителей, и что именно эта фирма преподносит в своих рекламных объявлениях (т.е. стратегия рекламного сообщения) [8]. К тому же, достаточно трудно отделить воздействие рекламы от всех прочих эффектов, которые влияют на объем продаж. Вообще, объем продаж — результат всей деятельности компании в сфере маркетинга и стимулирования сбыта, и, кроме того, он зависит от целого ряда условий "окружающей среды", таких, например, как действия конкурентов и многих других экономических, климатических, социальных и культурных факторов. Рекламу имеет смысл рассматривать в качестве единственного фактора, который определяет объем продаж, только при том условии, [c.559]
Вторая возможная реакция со стороны фирмы заключается в анализе имеющихся фактических данных, на основании которых фирма будет пытаться построить некую функцию отклика (или графическую зависимость), которая, несмотря на все имеющиеся трудности, будет связывать между собой расходы на рекламу и объемы продаж. После того как будет приблизительно определена форма такой кривой, ее можно использовать для определения того уровня рекламных расходов, при котором объем продаж (или относительный вклад в прибыль от сбыта продукции) максимален. Аргу- [c.560]
Все сведения об экономических, политических, социальных и других воздействующих факторах формируется в виде новой информации (1Н), которая сравнивается с уже имеющейся старой информацией (1С). Отклик социума на отношение 1Н/1С (на основании закона Вебера-Фехнера) выражается в виде логарифмической кривой (рис. 13.9). При 1Н / 1С = I > 1 параметр Щ находится на восходящей ветви а, при 1Н < 1 - на нисходящей ветви 6. Анализ логарифмической характеристики отклика человека на изменение I приводит к следующим выводам. Во-первых, при 1Н 1 изменение Щ пропорционально изменению I. Во-вторых, при значительной величине 1Н прирост Щ при одном и том же приросте 1Н / 1С меньше, чем при величине 1нв1- В-третьих, уменьшение 1Н (в границах 0<1Н<1) приводит к резкому увеличению отрицательной величины Щ. Таким образом моделируется более сильное воздействие на социум одной и той же величины кнута по сравнению с пряником . Кроме того, можно видеть, что постоянное увеличение пряника постепенно перестает приводить к заметному росту положительных результатов Щ. [c.231]
Однако главное затруднение в теории состоит в том, что во время бизнес-циклов малые изменения реальной заработной платы сопровождаются большими колебаниями выпуска и занятости. Для объяснения этого явления недостаточно, чтобы кривая предложения труда имела положительный наклон необходимо также, чтобы изменения предложения труда в ответ на рост заработной платы были весьма существенны. Возможен ли такой сильный отклик Сторонники теории реального бизнес-цикла утверждают, что возможен, если правильно интерпретировать понятие "отклик предложения труда". С их точки зрения, значительное изменение труда в ответ на малые изменения уровня реальной заработной платы есть следствие замещения труда во времени31. [c.582]
Для наших целей здесь важно отметить два момента. Первый связан с теорией, которая лежит в основе кривой Филлипса. Она была сформулирована Филлипсом (и еще ранее с меньшим откликом-Ирвингом Фишером (Fisher, 1926) просто как наблюдаемое статистическое отношение без особого обоснования с какой-то теоретической подоплекой. Липси впоследствии дал объяснение кривой как результата поведения рынка рабочей силы в условиях неравновесия. Его теория заключалась в том, что избыточный спрос на этом рынке ведет к росту номинальной заработной платы до равновесного уровня (и к снижению в результате избыточного предложения), что скорость корректировки, т.е. темп изменения номинальной за- [c.698]
