Диаграмма данного распределения представлена на рис. 2.8. Площадь каждого столбца диаграммы пропорциональна соответствующей вероятности. Например, площадь затемненного столбца составляет 12% от общей площади. Аналогично, площадь столбцов, отображающих три последние интервала (4000—, 5000— и 6000—), составляет 48% от общей площади. Такой подход — отличный метод определения вероятностей по распределению вероятностей. На рис. 2.9 представлена диаграмма, которая отражает альтернативный способ отображения тех же самых данных. Линейный график используется для очерчивания общей формы распределения, в то время как гистограмма очерчивает каждый интервал группировки отдельно. Этот график можно аналогичным образом использовать для отображения вероятностей. Пространство под линией можно использовать для определения вероятностей. Например, затемненный участок на рис. 2.9 показывает вероятность объема продаж свыше 4000 ф. ст. (т. е. всех значений вдоль горизонтальной оси, начиная с 4000 ф. ст.). Если мы примем, что общая площадь пространства под линией равна 1, тогда любой рассмотренный участок будет точно равняться вероятности. Так, затемненный участок на рис. 2.9 равняется 0.48 (48% от общей площади). [c.77]
Таким образом, со (Л) — это векторное пространство, порожденное столбцами матрицы Л. Размерностью этого векторного пространства будет г (Л). Имеем [c.28]
Доказательство. (П) => (i) Поскольку г(ЛЛ/ + ВВ/) = г(Л В), из (П) следует, что г (А В) = г (А) + г(В). Следовательно, линейное (под)пространство, натянутое на столбцы Л, и линейное пространство, натянутое на столбцы В, не пересекаются, т. е. со (Л) П ol(B) = 0 . [c.88]
Здесь, конечно, речь идет просто о порядке расположения чисел в числовом векторе-столбце иди -строке. В более глубоком представлении вектор однозначно определяет позицию точки в n-мерном евклидовой пространстве, т. е. задает направление отрезка, определяемом координатами точки в этом пространстве. [c.370]
В таблице 1.7 отведены столбцы только для двух конкурентов, что объясняется ограниченностью пространства на тетрадном листе. Если у вас конкурентов больше, постройте аналогичную таблицу с большим количеством конкурентов. [c.560]
Векторы a7, jel n будем называть векторами требований задачи (Д /), а вектор Ь — вектором ограничений. Множество всех неотрицательных линейных комбинаций столбцов а7 с геометрической точки зрения может быть представлено как многогранный выпуклый конус, натянутый на систему векторов а1 в пространстве Rm (рис. 1.3). [c.29]
Если некоторые т столбцов а 1 уа 2, ...,а от матрицы А являются линейно независимыми, то они образуют базис в пространстве / т, и их, вообще говоря, будет достаточно для представления вектора b в виде линейной комбинации указанных столбцов. Это означает, что остальные столбцы войдут в данное разложение с нулевыми коэффициентами. Если к тому же коэффициенты линейной комбинации окажутся неотрицательными, то мы получаем так называемый базисный допустимый план х, у которого не более т компонентов отличны от нуля. Сформулируем определение базисного плана более строго, так как это одно из фундаментальных понятий теории линейного программирования. [c.30]
Название метода произошло от понятия симплекса. Напомним, что т-симплексом называют выпуклый многогранник, аффинная оболочка 1 которого есть аффинное множество размерности т. В данном случае можно считать, что система расширенных базисных столбцов ал,а/2,..., а/т , рассматриваемых как точки в / m+1, порождает (т- 0-мерный симплекс в пространстве / от+1. [c.40]
Элементами (точками, векторами) вещественного векторного пространства Rn являются векторы-столбцы, состоящие из п вещественных чисел [c.485]
Теперь мы рассмотрим строение матрицы плана (т. е. расположение N экспериментальных точек в -мерном пространстве), для которого генератором служит наивысшее взаимодействие. Запишем матрицу плана полного факторного эксперимента для (k — 1) факторов. Эта матрица с 2k l строками и (k— 1) столбцами. Добавим столбец взаимодействия всех факторов, т. е. столбец [c.34]
В N-пространстве наблюдений показываются вектора-столбцы матрицы X. [c.13]
Если проводить рассмотрение в пространстве условий, то известно, что множество, образующее линейную оболочку векторов а - (где а,- -столбцы матрицы А), является выпуклым полиэдральным конусом. [c.206]
Word способен автоматическц устанавливать оптимальную ширину столбцов в таблице, т.е. такую, при которой текст в ячейке умещается на одной строке, не оставляя лишнего пространства. Выделите таблицу. В меню Таблица выберите команду Высота и ширина ячейки и в одноименном диалоговом окне щелкните на вкладке Столбец. Щелкните на кнопке Автоподбор. Ширина ячейки будет устанавливаться в зависимости от длины слова в ячейке. (Другой способ установить оптимальную ширину столбца дважды щелкнуть на одной из вертикальных линий сетки). [c.130]
Матрица размера т х 1 является точкой в пространстве Rmxl (т. е. в Rm) и называется вектором (вектор-столбцом) размера т х 1. Матрица размера 1 х п называется вектор-строкой размера 1 х гг. Элементы вектора обычно называются его компонентами. Матрицы обычно обозначаются заглавными буквами, а векторы — строчными. [c.23]
Ортогональность плана гарантирует отсутствие корреляции между факторами, поэтому кажется, что все оценки коэффициентов регрессии независимы и свободны от посторонних влияний. Однако это справедливо, если описываемая область факторного пространства действительно линейна (при данной ошибке опыта) и, следовательно, все члены уравнения, отражающие кривизну, имеют нулевые коэффициенты. В действительности кривизна может существовать, например, если интервалы варьирования велики и хотя бы некоторые коэффициенты при эффектах взаимодействия окажутся отличными от нуля. Тогда может получиться, что столбцы этих взаимодействий в матрице планирования будут закоррели-рованы с некоторыми столбцами линейных эффектов. В дробном факторном эксперименте, в отличие от полного, всегда существует такая корреляция хотя бы для некоторых столбцов. Это приводит к тому, что по результатам данного эксперимента оказывается невозможно разделить коэффициент регрессии между линейным эффектом и взаимодействием. Такие оценки называются смешанными (совместными), а сам факт корреляции — смешиванием. Смешиваемость оценок —дань за сокращение числа опытов. Экспериментатор может бороться со смешиванием путем уменьшения дробности реплики, уменьшения интервалов варьирования, выбора вида модели. Экспериментатор стремится к тому, чтобы максимальное число линейных эффектов оказалось не смешанным с парными взаимодействиями. Число линейных эффектов, которые не смешаны в данном плане, будем называть разрешающей способностью плана. [c.224]
Обозначим через а1 столбцы матрицы А и будем рассматривать их как векторы пространства Rm. Тогда каждому допустимому плану КЗЛП — я-мерному вектору х — соответствует неотрицательная линейная комбинация столбцов а7, равная столбцу be /Г [c.29]
На практике полная коллинеарность встречается исключительно редко. Гораздо чаще приходится сталкиваться с ситуацией, когда матрица X имеет полный ранг, но между регрес-сорами имеется высокая степень корреляции, т. е. когда матрица Х Х, говоря нестрого, близка к вырожденной. Тогда говорят о наличии мультиколлинеарности. В этом случае МНК-оценка формально существует, но обладает плохими свойствами. Это нетрудно объяснить, используя геометрическую интерпретацию метода наименьших квадратов. Как уже отмечалось, регрессию можно рассматривать как проекцию в пространстве Rn вектора у на подпространство, порожденное столбцами матрицы X. Если между этими векторами существует приблизительная линейная зависимость, то операция проектирования становится неустойчивой небольшое изменение в исходных данных может привести к существенному изменению оценок. Рисунок 4.1 наглядно это демонстрирует. Векторы у к у мало отличаются друг от друга, но в [c.110]
Конечномерные и бесконечномерные векторные пространства. Эквивалентные определения базиса. Равномощность любых двух базисов пространства размерность пространства. Возможность расширить до базиса любую линейно независимую систему векторов. Единственность разложения по базису и координаты векторов. Соответствие между действиями с векторами и со столбцами их координат. [c.10]
Эти множества, очевидно, не пусты (содержат неотрицательный ортант пространства переменых) и являются конусами. При этом К0(М) представляет собой конус, порожденный векторами-столбцами расширенной матрицы [c.13]
| Рисунок 8.З. Топография цен на двухкомнатные квартиры в Хельсинки Географическое пространство используется для анализа чувствительности при формировании цены. Данные взяты из портфеля, включавшего пять типов жилья обшей площадью от 40 до 60 м. Использовались четыре слегка отличных друг от друга СОК. Средняя цена за 1м вычислялась для 240 строк и столбцов На рисунке показаны только элементы изображения, находящиеся внутри допустимого интервала (1,6) по отношению к средней ошибке квантования множества обучающих примеров. Не показаны данные для рано нов с домами на одну семью и типовой застройкой, как на рис. 8 1 Наблюдения проводились с января 1992 г по март 1994 г Техническим исследовательским центром Финляндии | 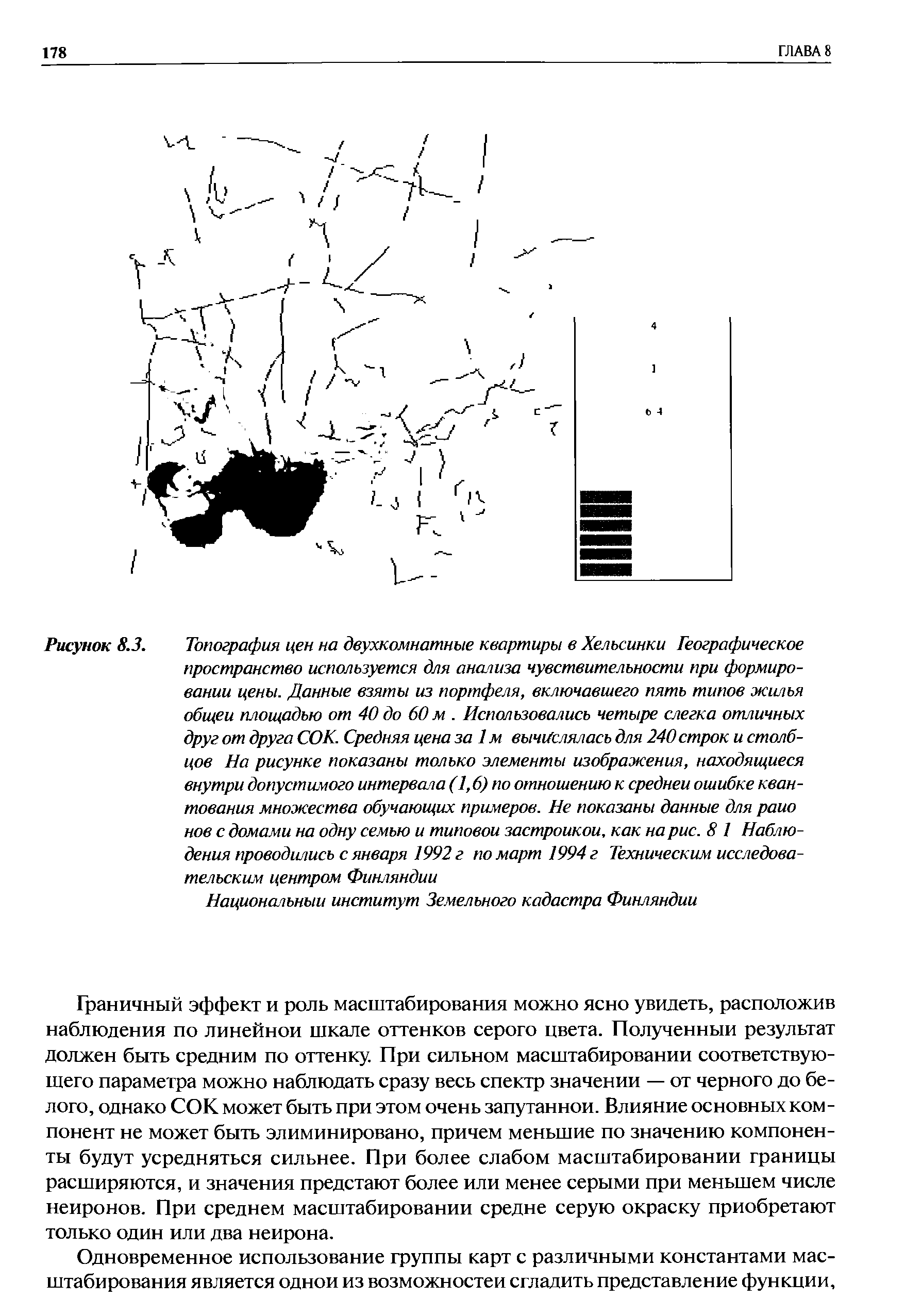 |
